A Simple Classroom Teaching Technique To Help Students Understand Michaelis-Menten Kinetics
Abstract
A new, simple classroom technique helps cell biology students understand principles of Michaelis-Menten enzyme kinetics. A student mimics the enzyme and the student's hand represents the enzyme's active site. The catalytic event is the transfer of marbles (substrate molecules) by hand from one plastic container to another. As predicted, increases in marble concentration increase the number of marbles transferred per unit time (initial rate, V0) until the turnover number becomes rate limiting and V0 approaches the maximum velocity (Vmax), as described by the Michaelis-Menten equation. With this demonstration, students visualize an important concept: the turnover number is constant and independent of marble concentration. A student assessment of this exercise showed that it helped students visualize the turnover number and Vmax but not Km, the marble concentration at which V0 is one-half Vmax. To address the concept of Km, we use supplemental laboratory and lecture exercises. This exercise with plastic containers and marbles is equally suited to demonstrate the kinetics of carrier-mediated membrane transport. We conclude that this exercise helps students visualize the turnover number and Vmax and gives students important insights into the kinetic parameters used to characterize the catalytic activity of enzymes and membrane transporters.
INTRODUCTION
Any cell biologist, biochemist, molecular biologist, or physiologist who teaches enzyme kinetics to undergraduate students knows what a daunting task lies ahead. Students are confronted with complex kinetic constants such as Km, Vmax, and turnover number, and these constants are based on rate constants, not the typical biology major's favorite concept. Because of the complex nature of the subject, many students come away from an introduction to Michaelis-Menten enzyme kinetics bewildered and utterly confused and avoid pursuing the subject in higher-level courses. This is unfortunate because Michaelis-Menten enzyme kinetics is the principle analytical method used to characterize the kinetic properties of enzymes and also that of membrane transport proteins (Van Winkle, 1999).
In our view, the concept of enzyme turnover number (the rate of a single enzyme's catalytic event) is essential to students' understanding enzyme kinetics and ultimately enzyme behavior. Hence, we have devised a simple, inexpensive classroom exercise that allows students in our junior-level Cell Biology course to actually view the turnover number as the enzyme catalyzes a hypothetical reaction: transfer of marbles from one plastic container to another by a student. Once students grasp the concept of turnover number and see that it is not influenced by substrate (marble) concentration, the instructor's task of teaching Michaelis-Menten kinetics becomes easier and, for the students, learning becomes more meaningful.
In many cell-based courses, such as cell biology, cell physiology, biochemistry, and physiology, membrane transport follows some time after the teaching of enzymes. Many membrane transporters behave as permeases and have several characteristics in common with enzymes (Van Winkle, 1999; Becker et al., 2006). For example, both have binding sites on their surfaces that bind substrate (enzymes) and solute (transporters), both lower the activation energy, both exhibit saturation with increases in substrate or solute concentration, and both exhibit kinetic constants, Km and Vmax. Not surprisingly the kinetics of solute transport by permeases can be modeled with the same system, marbles in plastic containers, as described for enzymes. In this manner, students gain a better understanding of transport kinetics and achieve a deeper understanding of the Michaelis-Menten equation as it applies to both enzymes and membrane transporters. Armed with this knowledge, students can pursue kinetics in higher-level courses and apply this knowledge to work on protein kinetics in biomedical research.
MATERIALS AND METHODS
The materials consist of two plastic tubs (35 × 24 × 12.7 cm deep), a stopwatch, marbles, and a student volunteer who represents the enzyme. Before we begin, the instructor draws analogies: 1) the student volunteer is the enzyme, as noted above; 2) one hand of the student grasps marbles and represents the enzyme's active site; and 3) the left plastic container contains substrate (marbles) and the right (receiving or product container) contains product of the reaction (Figure 1). Hence, the catalytic event is the transfer of a marble from the left container to the right container. The transfer of marbles by the student is represented in the following manner: 

Figure 1. The experimental system. (A) Materials needed include a timer, marbles, two plastic containers, and a blindfold. (B–D) Photographs depicting a student performing one 10-s “run” of the exercise. (B) Finding a marble in the “substrate” container. (C) Transferring a marble to the “product” container. (D) Releasing the marble into the “product” container. The 13-s video of the student performing the exercise is available (see Supplemental Material).
To determine Km, Vmax, and the turnover number, the substrate (marble) concentration is varied, usually from 5 to 30–40 marbles with the marble “concentrations” randomized during the experiment. Transfer of marbles from one container to the other takes place for 10 s; we call this V0 (initial rate) and assume that transfer takes place under initial-rate conditions. The instructor draws a graph on the board, and the data (V0) are plotted as a function of substrate concentration, the number of marbles.
RESULTS AND DISCUSSION
The Michaelis Constant, Km
We begin our analysis with the Michaelis-Menten constant, the Km or substrate concentration at which V0 is 50% of Vmax. Of the kinetic constants discussed in this article, Km is the most difficult for students to grasp (see Assessment below). Our objective with the introduction of this constant is threefold: 1) we show how it is determined from Figure 2; 2) we use the Michaelis-Menten equation to show why Km is determined when V0 is 50% of Vmax; and 3) we show that Km is useful as an index of affinity between substrate and enzyme only when a certain assumption is satisfied, as specified below.
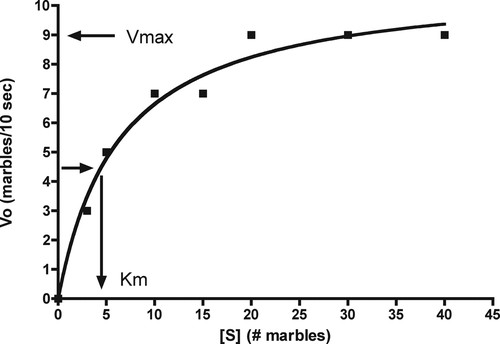
Figure 2. The rate of marble transfer (V0) from the substrate container to the product container depends on marble “concentration” in substrate (left) container. Assuming that Vmax is ∼9 marbles/10 s, Km, determined by interpolation, is ∼4.5 marbles.
Careful inspection of the Michaelis-Menten equation (Equation 1 below) shows that Km is added to the substrate concentration in the denominator. Therefore, Km must have units of substrate concentration and its value must be taken from the x-axis of Figure 2. Unfortunately, most students do not readily realize this fact. We emphasize this point that Km has units of substrate concentration by showing why Km is the substrate concentration at which V0 is one-half Vmax. In doing this, we introduce the students to the Michaelis-Menten equation: 
If we set [S] = Km, the Michaelis-Menten equation reduces to 
Our final issue concerning Km is its meaning. We have defined Km above, but this definition has an additional meaning when a specific assumption is satisfied: Km becomes a dissociation constant such that larger Km values mean lower affinity between substrate and enzyme and smaller Km values mean the opposite, higher affinity. But at this point we have to resort to use of rate constants, in spite of student abhorrence of these constants, to achieve a deeper understanding of Km as an index of affinity. As above, for an enzyme-catalyzed reaction we write 
where k1 and k−1 are rate constants for the forward and reverse reactions between substrate and enzyme, respectively. The dissociation constant (Kd) for the interaction between enzyme and substrate is defined as follows (Stryer, 1995): 
But, for an enzyme-catalyzed reaction, the ES complex converts to Ef + P, the product of the reaction, and this part of the overall reaction has its own rate constant k2, the turnover number. Note that k−1 and k2 have a common intermediate, ES, and are therefore additive. Because ES can dissociate to either Ef + S or Ef + P, the Km is defined as follows: 
If we are to interpret Km as a Kd (dissociation constant), then 

Now Km ≈ Kd and Km can be treated as an affinity constant (Stryer, 1995).
Turnover Number, Saturation, and Vmax
As predicted, V0 increases with increases in marble “concentration” until the enzyme becomes saturated with substrate (marbles) at approximately 20 marbles (Figure 2).
At this point we define the turnover number: the number of substrate molecules catalyzed per second per enzyme molecule when the enzyme is saturated with substrate (Nelson and Cox, 2005; Becker et al., 2006). Hence, when the enzyme is saturated with substrate the turnover number (k2) becomes rate limiting. Next, we ask the class if the turnover number or the rate of marble transfer from one plastic container to the other depended on the number of marbles present in the substrate container? They see that it does not and answer no. This is a crucial student observation because it shows that V0 increases because the probability of enzyme finding substrate increases with higher substrate concentrations: V0 does not increase because higher substrate concentrations increase the turnover number; in our experience this is a too often encountered student misunderstanding.
Our next question to the students follows from the first. We ask what limits the catalytic rate at high substrate concentration when V0 has leveled off? Some astute students will answer that the turnover number limits V0 because they saw that the enzyme's turnover number is fixed, no matter the substrate concentration: The student who mimics the enzyme can move his/her hand only so fast. At this point, we emphasize that marble transfer consists of two components: 1) “to-find” time and 2) transfer or catalytic time. To emphasize this point, we have the students plot to-find + transfer time (called total time) as a function of marble “concentration.” To do this, they take the reciprocal of V0 (to simplify matters, we change V0 units to marble per second before doing the calculation). These data represent the time it takes the student to find and transfer a marble from the substrate to the product container (Becker et al., 2006). Note that total time decreases exponentially as marble “concentration” increases (Figure 3). The students are aware that the turnover number (transfer time) is fixed, and therefore the decline in total time must be due to a decline in to-find time. Further, with increases in marble concentration the line becomes asymptotic because the turnover number becomes rate limiting (Becker et al., 2006). The reciprocal of the asymptote (0.9) gives the turnover number, 1.1 marbles/s. Thus, the catalytic event, transfer of a marble from substrate to product container, takes ∼1 s.
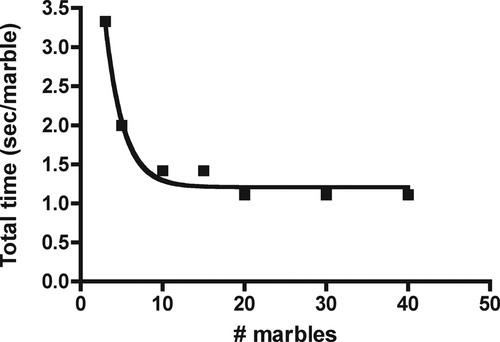
Figure 3. Total time (to-find + transfer time) is plotted against the number of marbles. To calculate total time, we changed V0 to marbles per second and then took the reciprocal of these data. The line approaches an asymptote because the turnover number becomes rate limiting. The reciprocal of the asymptote approximates the turnover number. The line fit to the data points is a one-phase exponential decay curve.
Now we are ready to introduce the concept of saturation and to write an expression for maximum velocity (Vmax). At this point students also realize that the enzyme has a Vmax because there are a limited number of enzyme molecules catalyzing the reaction and that the enzyme is saturated with substrate. Under this condition, when [S] ≫Km, the Michaelis-Menten equation reduces to the following: 

Lineweaver-Burk Plot
Having explored the meaning of Km and Vmax, we then introduce the Lineweaver-Burk double-reciprocal plot (LB plot) to obtain values for Vmax and Km. Plots of V0 against substrate concentration do not always saturate because saturating concentrations of substrate are not used and other methods, such as the LB plot, must be used to determine the kinetic constants (Becker et al., 2006). The advantage of the LB plot is that it straightens out the curvilinear kinetic curve of Figure 2. In the LB plot, Km is derived from the negative x-axis intercept, and Vmax is obtained from the y-axis intercept (Figure 4). Now the students are ready to perform an LB plot with the trypsin data collected in laboratory (see Supplemental Exercises below) and to determine the enzyme's kinetic constants. Once students have acquired their kinetic constants, we have them use the Michaelis-Menten equation, their substrate concentrations, and their Vmax and Km values to generate a kinetic curve and compare it with the experimentally derived curve. This allows them to assess the quality of their graphically determined kinetic constants, Km and Vmax. This exercise also gives the students practical experience with the Michaelis-Menten equation and shows how the kinetic constants relate to and limit V0.
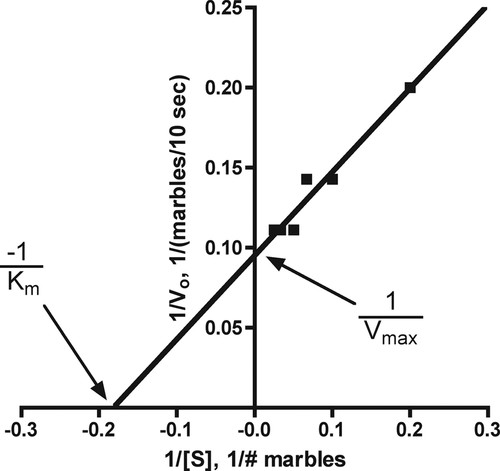
Figure 4. A Lineweaver-Burk double-reciprocal plot of the data collected from transferring marbles from substrate to product plastic container. The x-axis intercept is the negative reciprocal of Km, ∼5.6 marbles, and the y-axis intercept is the reciprocal of Vmax, ∼10.5 marbles/10 s. Both kinetic constants are in reasonable agreement with those determined from Figure 2: Km is ∼4.5 marbles and Vmax is ∼9 marbles/10 s.
Questions
At this point, we ask the students several questions to test their understanding and to show how cells regulate enzyme catalytic activity. First, we ask how can cells increase Vmax of an enzyme-catalyzed reaction? Examination of Equation 6 shows that cells may increase either k2 or Et. We point out that k2 could be modulated by positive feedback regulation, whereas increases in Et require increases in enzyme synthesis. Second, we ask if either of these cellular “strategies” influence Km? This is a challenging question because increases in Vmax are perceived by many students to also change Km. However, neither of these strategies influences Km because they do not influence the affinity of enzyme for substrate. For example, if cells synthesize a new enzyme, it will be structurally identical to the original enzyme and the active site does not change; therefore, the Km for the new enzyme molecules is the same even though Vmax increased. Third, we ask if the enzyme and substrate to-find time (time to find one another) changes as substrate concentrations increase. The students observed a decrease in to-find time as substrate concentration increases. Importantly, this reinforces the notion that increases in V0 are achieved by increases in probability of encounter between substrate and enzyme and not by increases in k2.
Supplemental Exercises
To supplement this approach to teaching Michaelis-Menten enzyme kinetics, we derive the Michaelis-Menten equation according to Turrens (1997). This simple derivation gives students insight into the origins of the equation and a more meaningful understanding of this important expression. In laboratory we use the enzyme trypsin (Sigma, St. Louis, MO) to couple the analysis presented here with laboratory exercises that teach students the importance of initial-rate measurements in enzyme kinetic studies. Then students explore the effects of increases in both trypsin and substrate concentration on V0 and analyze their data with an LB plot.
Application to Membrane Transport: Analysis of Permease Activity
In the course of developing this teaching technique, we became aware that it also applies to membrane transporters, especially facilitated carriers (permeases; Van Winkle, 1999; Becker et al., 2006). The same analogies described above apply to transporters: the student is the transporter and one hand is the transporter's solute-binding site. In this case, the catalytic event is marble transfer from the outer (left) compartment to the inner (right) compartment (Figure 1). We assume that transfer is unidirectional (out-to-in, called Ji) and both intracellular (inner) and extracellular (outer) solute concentrations do not change during the flux measurement. The “reaction” for facilitated transfer of solute across a membrane is identical to that for enzymes: 


From this analysis some students realize that the Kt for solute influx and efflux are the same for facilitated carriers that are incapable of active transport. By extending this analysis to membrane transporters students gain a deeper appreciation of Michaelis-Menten kinetics and see that the analysis and equations actually apply to a wide variety of functional proteins.
Assessment
To assess whether this teaching technique facilitated students' understanding of Km, Vmax, and turnover number, we had the students (n = 34; junior-level Cell Biology class) indicate the helpfulness of this exercise on an anonymous assessment form composed of six questions (summarized in Table 1). The data were analyzed using a 2 × 3 contingency table to determine if the exercise helped students both visualize and understand the kinetic parameters of the Michaelis-Menten relationship. For the analysis we pooled the “greatly helped” and “moderately helped” groups together into one group (“helped” group), and the “did little to help” and “did not help” groups into another group (“did not help” group) to enable us to test the hypotheses that 1) this exercise helped students visualize Km, Vmax, and turnover number, and 2) this exercise helped students understand Km, Vmax, and turnover number. The Chi-square analysis (SigmaStat statistical software; Aspire Software International, Ashburn, VA) showed that this exercise effectively (p < 0.05) allowed students to visualize Vmax and the turnover number, but not the Km. Similarly, the exercise increased students' understanding (p < 0.05) of the Vmax and turnover number, but not Km. These data suggest that the visualization of the exercise increased the understanding of Vmax and turnover number.
| Questions | Greatly helped | Moderately helped | Did little to help | Did not help |
|---|---|---|---|---|
| Did the exercise help you visualize the idea of Km? | 3 | 14 | 13 | 4 |
| Did the exercise help you visualize the idea of Vmax? | 9 | 14 | 10 | 1 |
| Did the exercise help you visualize the idea of turnover number? | 16 | 11 | 5 | 2 |
| Did the exercise increase your understanding of Km? | 3 | 10 | 13 | 8 |
| Did the exercise increase your understanding of Vmax? | 6 | 15 | 8 | 5 |
| Did the exercise increase your understanding of turnover number? | 15 | 7 | 7 | 5 |
CONCLUSIONS
The approach to teaching Michaelis-Menten kinetics described in this article, coupled with laboratory exercises and Turrens derivation of the Michaelis-Menten equation, gives those students who are willing to learn a unique opportunity to “come-to-grips” with this difficult subject. As noted above, we use this approach in our junior-level Cell Biology class for biology majors. In our view, and supported by our assessment of this exercise, the single most important innovation with this teaching technique is student visualization of the turnover number and that this constant is independent of substrate (marble) concentration. Everything else follows from this concept. Of course, some students are resistant to any approach that involves kinetics of cellular processes, but for many students this approach does work and provides a solid foundation for the pursuit of kinetics in higher-level courses in biology, biochemistry, molecular biology, and physiology.