Introductory Life Science Mathematics and Quantitative Neuroscience Courses
Abstract
We describe two sets of courses designed to enhance the mathematical, statistical, and computational training of life science undergraduates at Emory College. The first course is an introductory sequence in differential and integral calculus, modeling with differential equations, probability, and inferential statistics. The second is an upper-division course in computational neuroscience. We provide a description of each course, detailed syllabi, examples of content, and a brief discussion of the main issues encountered in developing and offering the courses.
INTRODUCTION
We describe two efforts to improve the mathematical, statistical, and computational training of undergraduates in life science majors at Emory College.
Description of Objectives
The Mathematics and Computer Science and the Biology Departments both offer courses that provide mathematical, statistical, and computational instruction for life science majors at Emory College. An introductory sequence is intended for freshmen with good high school mathematics background and has been taught by mathematics and computer science faculty for almost 15 yr, in various forms. It provides the quantitative training needed by all life science students and is required by the Department of Biology for its Bachelor of Science program. For quantitatively intense subdisciplines, the Department of Biology has upper-division courses in modeling and computation. We describe one course, in computational neuroscience, that has been offered for the past 3 yr.
Curricular and pedagogical issues in preparing life science students for an increasingly quantitative set of disciplines have several consistent themes. Our introductory mathematics sequence for life science majors, Mathematics 115/116-Life Science Calculus 1/2, addresses two of these themes.
First, mathematical, computational, and statistical methods are of ever-growing importance in the life sciences. We introduce the basic quantitative tools required in modern life science research, adhering to the recommendations of the National Research Council report BIO2010 (National Research Council, 2003) and the Mathematical Association of America's Math & Bio 2010 (Steen, 2005). Consequently, introductory quantitative course work should include modeling change in biological systems via discrete dynamics, continuous differential equations (DEs), and stochastic processes; and organization and analyses of data in information-intensive fields such as molecular evolution and genetics.
Second, researchers in the biological sciences and also health science professionals must be discerning readers of the research literature. In particular, critical evaluation of, and conclusions drawn from, mathematical models and statistical studies is indispensable. These require experience constructing and criticizing models of biological phenomena and an understanding of probability theory, as the underpinning of inferential statistics, and exposure to statistical methods used to establish confidence and test hypotheses.
Preparation of majors for graduate programs in highly quantitative subdisciplines is also of growing importance. For students involved in computational neurobiology or population biology, for example, appropriate course work must be designed. Mathematical Concepts in the Neurosciences (MCN) at Emory College provides an example of such a course. Neuroscience is rapidly becoming one of the most quantitative biological fields. An increasing number of research papers in neuroscience combine results of experiments and computer simulations of mathematical models. MCN focuses on several seminal mathematical models used in neuronal coding, neuronal and network dynamics, and learning in neuronal networks. The main objective of the course is to develop in students the ability to interpret, analyze, and develop these models. A secondary objective is to stimulate a deeper understanding and active use of the mathematical concepts used in the formulating and analyses of models. A brief syllabus of MCN is provided in Mathematical Concepts in Neuroscience.
Main Challenges
Concerning the introductory sequence, it is now the main mathematics requirement for the biology major. Unfortunately, student math background and aptitude vary widely. We attempt to balance continuity with high school math training, as varied as it is, with emphases on modeling and problem solving, which are usually new to our students. To manage quite demanding syllabi, there is a mandatory additional contact hour that allows review of material, question-and-answer, and more frequent testing; so, students have 3 lecture hours and 1 lab hour each week. And Emory College offers a supplemental instruction program based on peer tutoring, an important resource. Substantial integration of life science topics is key both to the educational purpose and to student interest. This has been underscored with presentations by biology faculty on topics such as population biology and modeling physiological systems such as the neuron. In teaching inferential statistics, it is important to emphasize experimental design and to use real experimental data.
Coordination of several text and Web sources is required. Unlike the situation in physics-oriented calculus education, there are not many texts that address the range of topics required. The choice of proper content and textbooks for MCN is also a challenge. There are several excellent textbooks on the application of mathematical methods in the neurosiences, including Foundations of Cellular Neurophysiology (Johnston and Wu, 1995), Computational Cell Biology (Fall et al., 2002), and Mathematical Physiology (Keener and Sneyd, 1998). From our perspective, the most balanced representation of mathematical concepts used in the modern neurosciences is presented in Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems (Dayan and Abbott, 2001). For example, Dayan and Abbott consider not only excitability of individual neurons and dynamics of activity in neuronal networks but also information-theoretic approaches to neuronal code and learning in neuronal networks—important themes that are often underrepresented in textbooks. Dayan and Abbott clearly demonstrate how a mathematical approach helps to solve many fundamental problems in neuroscience. Unfortunately, mathematics is just used and not discussed in the book. Our challenge is to retain the research spirit of the book but adapt the content to undergraduates who have just begun to understand the role of mathematics in neuroscience.
We have chosen Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems as a main textbook. However, during the course we referred to other textbooks on specific topics. For example, when considering modeling neurons with simple nondifferential equations, we used some models and diagrams from Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (Izhikevich, 2010).
Another challenge is building adequate enrollment. MCN is an elective course. It has to compete for students with many well-established courses that do not “scare” biology students with mathematics. The health career focus of the majority of majors presents a real challenge. It is hoped that courses such as MCN, supported by the introductory sequence and early independent research opportunities, will be useful in attracting more students intent on science graduate programs, as well as changing the ambitions of current students.
INTRODUCTORY MATHEMATICS SEQUENCE FOR LIFE SCIENCE MAJORS
In this section, we describe several versions of the year-long Mathematics 115/116-Life Science Calculus 1/2 that have been taught at Emory over the past 14 yr.
In the early 1990s, the Science and Mathematics Departments at Emory College were meeting regularly to discuss Science 2000, an ambitious faculty, program, and infrastructure development plan. We were eager to expand our majors, individually and in collaborative interdisciplinary programs. We also wanted to modify the premed orientation of the strong majority of lab science majors and to attract more students to our majors intent on graduate education in what have come to be called the science, technology, engineering, and mathematics (STEM) disciplines. Even 20 yr ago, it was obvious that the life sciences were being transformed by the essential use of mathematics, statistics, and computing and that the standard physics-based calculus sequence did not provide the right quantitative training for life science majors.
Early Versions of the Sequence
We began in 1997–1998 after extended discussions with faculty in biology and biostatistics.
Version 1: 1997–1999. Main reference: Mathematics for the Biosciences (Cullen, 1983). The two-course sequence was purposely designed to have the first term quite similar to Calculus 1, so that students could switch freely between the standard Math 111/112-Calculus 1/2 and the life science sequence. The second course was substantially different from standard Calculus 2, substituting DEs, discrete probability, and inferential statistics for integration techniques and series and sequences.
The course was designed with input from the Department of Biology and was recommended by it for its majors, but it was not required. Enrollments in 1997–1998 in 115/116 were 28/12 and increased the next year to 48/20 students. The course was taught in two small sections each fall, with one section in the spring. During the same years, enrollments in standard, business, and Advanced Placement (AP)-based calculus were approximately 400–500.
The department was pleased with the initial offerings but not with the available texts. We found it difficult to maintain enough similarity with Math 111 to allow students to switch between sequences and to introduce interesting life science applications. Enrollments were disappointingly low, because the courses were not well enough publicized and although recommended by the Department of Biology, they were not required by any majors.
Version 2: 1999–2007. Main reference: Modeling the Dynamics of Life: Calculus and Probability for Life Scientists (Adler, 1989, 2005). The text and syllabus marked a substantial departure from the original objective of keeping the first term close to Calculus 1. Adler begins with a precalculus review and an introduction to discrete dynamics. This is followed by differential calculus and then by applications featuring the relationship between the derivative and stability of equilibria. DEs and definite and indefinite integrals complete the first course. Substantial modeling topics are included throughout the syllabus.
The second term begins with more DEs, including equilibria and stability for autonomous DEs. Systems of DEs and the phase plane are used to model competition, predator–prey interactions, and epidemics. An ambitious model of the neuron concluded the DE modeling segment of the second term, approximately one-third of the course. This was followed by an introduction to probability and descriptive statistics, discrete and continuous random variables, the binomial and normal distributions, and the central limit theorem (CLT). Inferential statistics, featuring estimates of the mean, confidence intervals, and hypothesis testing, are the last topics.
During summer 2003, with a grant from the Faculty Science Council and College Center for Science Education, the sequence was revised to include a MATLAB (The MathWorks, Natick, MA) component. This was used for both modeling and statistics. The department has an instructional computer lab with 32 networked work stations that allowed MATLAB training and assignments.
During this period, enrollments grew to almost 100 in the fall term, taught in several small sections, with never >50 in the spring. Instructors were pleased with the evolving syllabus and choice of topics. However, students were not so happy about the introduction of MATLAB. The course became difficult to offer logistically and just a bit overwhelming. Although the courses were still not required by any of the life science majors, Department of Biology advisors strongly suggested the sequence to freshmen and continuing students who had delayed taking mathematics.
Version 3: 2007–2008. Main references: Mathematical Models in Biology (Allman and Rhodes, 2004), Calculus Lite (Morgan, 2001), and Chance in Biology: Using Probability to Explore Nature (Denny and Gaines, 2000). This was the most significant departure from standard calculus that we attempted. We used Mathematical Models in Biology (Allman and Rhodes, 2004) to introduce topics such as population dynamics and initially study them with discrete difference equations. Calculus was introduced, as needed, to understand continuous change. In term 1, we developed discrete and continuous models of populations, infectious disease, and predator–prey systems. These were analyzed with cobwebbing and phase lines; stability of equilibria was determined with the derivative. After introducing the integral and DEs, we saw how autonomous DEs provide continuous versions of the previous population models.
Term 2 began with systems of DEs, including predator–prey and the susceptible-infected-recovered (SIR) model of epidemics. Phase planes and slope fields were used to provide qualitative information about solutions. Probability and statistics were then motivated by genetics and molecular evolution. Probability topics included Bayes theorem, rare disease examples, discrete and continuous random variables, binomial and geometric distributions, the normal distribution, and the CLT. Statistical methods included descriptive and inferential statistics, with emphasis on hypothesis testing, sampling distributions, and analysis of variance.
MATLAB was an important demonstration tool in the course, in part because it is used extensively in the Allman and Rhodes (2004) textbook. We had more opportunity for this because an extra lab hour was added to the course in 2007–2008, a feature that we have retained. Students in each lecture section (approximately 40 in each of two) are divided into two labs that taught by the same lab instructor.
Both course instructors were pleased with the syllabus. Presenting students with both discrete and continuous versions of the same models seemed to work well. This provided invaluable exposure to modeling and problem solving. However, several organizational issues forced us to return to a more standard syllabus. First, the Department of Biology (finally) decided to require the sequence for its B.S. degree program. This meant that we needed to accommodate more students, with more varied backgrounds. It was decided to allow students with AP Calculus credit to place out of Math 115 and enroll in Math 116 in the spring term and to allow students to switch from Math 115 to Math 112. This required that Math 115 topics more closely approximate Math 111 and that Math 116 not presume exposure to discrete dynamics. In fact, discrete dynamics has, essentially, disappeared from the first-term course and is mentioned only briefly in comparison with DE modeling in the second term. The next section contains a detailed description of the course as it exists now.
Concerning enrollments in these versions of the course, the Department of Biology graduated ∼100 students per year between 2000 and 2009, with a high of 132 and a low of 92. Numbers in the 1990s were somewhat higher—the Neuroscience and Behavioral Biology Program (subsequently becoming a department) has attracted many majors, some away from biology. It is difficult to get an accurate estimate of the proportion of biology majors who took the 115/116 sequence as their main college mathematics in the past. It may be possible to query the registrar's databases to compare grades of biology graduates in specific quantitatively intensive life science courses who took Math 115/116 with those of students who took other, or no, mathematics courses. The results would be confounded to some extent by precollege mathematics background.
Math 115: Life Science Mathematics 1
Below are the main topics in the current first-semester syllabus.
Precalculus review including trigonometric, exponential and logarithmic functions, exponential growth, and decay models.
Introduction to differential calculus, including transcendental functions and applications of the derivative to optimization and graphing, higher-order derivatives, emphasis of growth models including logistic growth, optimal foraging, and Newton's law of cooling.
Introduction to integral calculus including antiderivatives, definite integrals, Riemann sums, and the fundamental theorem of calculus, integration by substitution and by parts, area under the curve, and volume of a solid, improper integrals.
Introduction to differential equations, separation of variables, equilibria of autonomous DEs, simple epidemic model, and more growth models.
Math 116: Life Science Mathematics 2
Below are the main topics in the current second-semester syllabus.
Systems of differential equations, particularly predator–prey systems, models of species competition, and the SIR model of infectious disease. Slope fields and phase plane diagrams describe the qualitative behavior of solutions.
Introduction to matrices and partial derivatives. Use of the Jacobian to describe the type and stability of equilibria of systems and the shapes of trajectories.
Introduction to probability theory, motivated by genetics and molecular evolution, including: discrete spaces, conditional probability, rare disease examples, discrete random variables, binomial and geometric distributions, continuous random variables, probability density functions, the normal distribution, and the CLT.
Introduction to statistical methods: descriptive and inferential statistics, with emphasis on confidence intervals and hypothesis testing, sampling distributions, and analysis of variance.
Additional material may include probabilistic topics such as random walks applied to diffusion and genetic drift, and statistical tools such as the chi-square test, contingency tables, goodness-of-fit, and nonparametric tests.
Examples from the Course
We illustrate the level and focus of the courses with two sets of examples drawn from the current syllabi of the two courses: modeling biological systems with DEs and the CLT and sample means.
Modeling Biological Systems with DEs. In Math 115, we develop various population models, beginning with exponential and logistic growth. Optimization applications include optimizing food intake of bees and maximizing a sustainable fish harvest. Autonomous differential equations are illustrated with Newton's law of cooling.
Systems of autonomous DEs are introduced in Math 116—basic predator–prey models provide an important example. Let p = p(t) and q = q(t) be two populations described by 
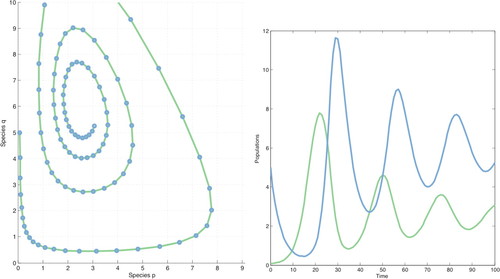
Figure 1. Numerical methods and MATLAB yield the trajectory on the left and the solution curves on the right. There is also Web-based direction field software that will draw trajectories. This allows easy experimentation with different initial conditions and with varied constants in the equations.
This is one of three models of biological systems that we study in the first part of Math 116. This is based on extensive discussion of exponential and logistic growth in Math 115. It requires a brief introduction to two-variable functions, partial derivatives, and very basic matrix theory, including eigenvalues and eigenvectors. The qualitative description of trajectories also is applied to competition models and to the SIR epidemic models. We use Web materials developed at Duke (CCP materials, www.math.duke.edu/education/modules2/materials), particularly for the epidemic models.
CLT and Sample Means. Probability theory is easily linked to a variety of life science topics. Conditional probability, Bayes' theorem, and rare disease examples provide one of the most accessible and surprising applications. In Math 116, we do enough probability theory to discuss random variables and several distributions. We illustrate the discrete geometric and binomial distributions with several life science examples, notably topics in genetics such as the Hardy–Weinberg law. The Poisson distribution is very important in understanding biological processes and provides a link between discrete and continuous distributions. Aside from the normal distribution, we also discuss the memoryless exponential distribution.
The CLT links probability theory and the main tests of inferential statistics, a powerful mathematical tool that we repeatedly emphasize in the course. It asserts that if sufficiently large random samples are drawn from a population then the distribution of sample means is approximately normal. In Figure 2 we display this using the exponential distribution with parameter λ = 0.2 and hence mean μ = 5 and variance δ2 = 25. Note the change from an exponentially shaped curve with n = 3 to an approximately normal curve with n = 30. We show how the CLT supports the use of confidence intervals and of hypothesis tests such as the z test and t test. We do not develop the theory behind the chi-square test but it is used to test compound hypotheses. When time allows, we also consider tests of paired data.
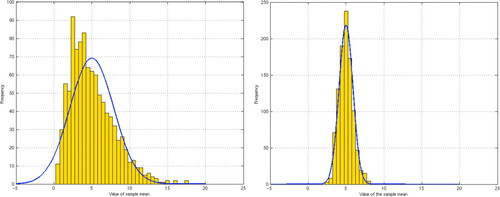
Figure 2. Left, sample size, n = 3. Right, n = 30, with a very close fit to the normal curve predicted by the CLT. Can we approximate the variances for each? Can we account for the difference in variances?
Issues and Future Directions
There are several issues that we continue to face in offering this course. As noted, biology majors bring substantial variation in mathematical background and aptitude. Calculus is not a prerequisite for the sequence. However, students who enter Emory College without calculus usually have spotty math background and weak skills. Conversely, students with extensive high school math, such as the BC version of AP Calculus, have quite clear ideas about what math is all about. They can be resistant to new topics and new foci on model building. Dealing with a heterogeneous population and maintaining a balance between a challenging course and realistic expectations will always be an issue with an introductory math for bio sequence.
An important related point is that this is a mathematics sequence, taught by math faculty. Even math faculty who do very applied work want to introduce the required theory. For example, analysis of equilibria and trajectories of solutions of systems of DEs requires enough matrix theory to talk about eigenvalues and enough about approximation through linearization to justify conclusions based on the Jacobian of partial derivatives. And the CLT is a mathematical gem that supports the tests of inferential statistics. We could spend considerably more time on learning recipes if we did not develop the mathematics required for qualitative analysis of equilibria or the CLT.
It is important to introduce students to appropriate computational software. A graphing calculator and a spreadsheet program such as Excel (Microsoft, Redmond, WA) are adequate for almost all the statistical material. But it would be useful to reintroduce MATLAB into the courses in order to solve larger linear systems and to obtain numerical approximations.
The main text (Bittinger et al., 2006) is adequate for the first term as it now is defined. There is no text at the right level that provides the calculus, probability, and inferential statistics material. The Adler text (2005) has just about the right mix but does not do a good job of presenting inferential statistics in a concise, readable way. Over the past couple of years, we have consolidated the material for Math 116 but we would still prefer a single text, or pair of inexpensive texts, for the sequence.
There are at least two strategies for improving this course sequence. First, we can strengthen the internal organization of the courses. For example, population models could be more realistically developed, based on a more thorough grounding in population biology. The predictions of our models could then be tested using the statistical methods we later study. Second, there is a great deal to be gained by linking our syllabus with those of related life science courses. If, for instance, our presentation of probability could be coordinated with the right topics in the genetics course, there would be mutual reinforcement. Given the way students take courses—and departments organize them—this sort of cooperation is very difficult. This is one of the reasons that science educators are intrigued by interdisciplinary introductory science courses.
MATHEMATICAL CONCEPTS IN NEUROSCIENCES
Life Science Mathematics 1 and 2 develop a background to teach mathematics related to specific areas of life sciences. Along these lines, we developed the MCN course. This is a course for majors in biology and in neuroscience and behavioral biology. In what follows, we describe the main ideas behind the syllabus of the course, the syllabus itself, and some of the hands-on experience.
Problem-driven Mathematics
In the course, mathematical concepts are introduced in a problem-driven way. We start with real biological problems and discuss appropriate mathematical models of the processes considered. Students engage their biological expertise and think about the meaning and strengths and weaknesses of mathematical models. Then, they are presented with the mathematical apparatus necessary for the model analysis.
Neuroscience has quite a number of problems that have been critically advanced by using mathematical models. We do not pretend to cover them all. Rather we strive to select such a sequence of problems that allows us to use simple mathematics first and then gradually increase the complexity, and to use mathematical concepts repetitively, so that the students could understand them more deeply and learn to use them in different contexts.
The course is intense. To quickly and clearly present biological problems, experiments, data, and mathematical models, we use a lot of slides. Some of these slides are available at a WikiFuse site (to which we contribute) at http://wikifuse.pbworks.com/browse/ and select Math for Neuroscience. Although the problems are drawn from the neurosciences, it should be clear from the syllabus below that the mathematical models and methods considered are quite general and are fundamentally important for other areas of biology as well.
Syllabus
The structure and main items of the MCN syllabus are presented in Table 1. As the table shows, some themes are repeated. First, these are the basic characteristics of random variables such as the mean and variance. They appear as an initial description of experimental spike time series. Later, these characteristics are calculated for the binomial and Poisson distributions. Stable steady states of ordinary differential equations (ODEs) are considered multiple times: initially while deducing the equations of ionic channel kinetics (Hodgkin and Huxley, 1952), then by exploring steady states of neuronal activity, and finally while considering a network model in which stable steady states model memorized items. Matrices and vectors also are used in various contexts starting from simplest descriptions of population activity through the analyses of network dynamics.
| Area | Problem | Mathematical concept |
|---|---|---|
| Neuronal coding | Characterization of neuronal spikes | Elementary statistics, time averaging |
| Entropy and information in spikes | Binomial and Poisson distributions, entropy, mutual information, stochastic processes, Poisson process | |
| Neuronal dynamics | Membrane excitability | ODEs and their solutions, phase space |
| Steady state activity | Stable and unstable steady states of dynamical systems | |
| Periodic neuronal dynamics | Stable and unstable periodic solutions of dynamical systems, Poincaré mapping, bifurcations | |
| Neuronal morphology | PDEs and their solutions, linear cable equation and its solutions | |
| Neuronal network dynamics | Lyapunov function | |
| Learning in neuronal networks | Synaptic plasticity | Time averaging, matrices, orthogonality of vectors |
Examples from MCN Course
The following examples illustrate the problem-driven approach to introducing mathematics in the MCN course. The first example deals with the analysis of experimental data on activity of hippocampal neurons. The hippocampus is a brain structure that is critically involved in learning and memory. The understanding of the hippocampal functioning gained a lot from hippocampal cell recordings in rats. In particular, experiments with navigating rats revealed that hippocampal cells encode the spatial context of the behavior (O'Keefe and Dostrovsky, 1971). In a typical experiment, a rat with chronically implanted electrodes forages for food pellets. Pellets are dropped to random locations of the arena by an automatic feeder. During a sufficiently long recording (>10 min), the rat visits most locations of the arena multiple times. Remarkably, many hippocampal cells spike only in some parts of the arena, specific for each cell. Figure 3 shows the data for two such cells. The left column of the figure represents the firing rates of the cells. The firing rate in a location (here a 2- × 2-cm square) is defined simply as a ratio of all the cell spikes observed while the rat was in the location to the total time the rat spent in the location. The figure shows that the peak firing rates of the cells are quite similar. The rat hippocampal cells presumably encode not only animal locations. Do these two cells encode different information? To determine other correlates of the cell spiking, more sensitive measures of cell activity are necessary.

Figure 3. Information versus firing rate. Two hippocampal cells, cell 1 (top row) and cell 2 (bottom row), fired only when the foraging rat visited specific parts (red spots) of the circular arena. Although their peak firing rates were similar (left column), the information measure of spiking, Ipos was not (right column), indicating important distinction between the information processing in these two cells (adapted from Olypher et al., 2003).
Indeed, the firing rate is an estimate of the mean of the distribution of spike counts observed in the time bins when the rat was in the location. One therefore may think of measures that take into account other properties of this distribution. One such measure follows from averaging the difference between the uncertainty −log P(k) of observing k spikes in an arbitrary time bin and the uncertainty −log P(k|xi) of observing k spikes in location xi: 
The second example relates to the problem of neuronal dynamics. Analysis of dynamical equations provides deep explanation of possible regimes of neuronal activity and transitions between them. In the example, we consider the classical model of excitable membrane by Morris and Lecar (1981). The model describes the time evolution of the electric potential across the membrane of barnacle giant muscle fiber. The membrane has two ionic currents, potassium and calcium. The model is a system of two autonomous nonlinear DEs. Among the parameters of the system are the maximal conductances of the ionic currents ḡK and ḡCa. These parameters can be increased or decreased in the experiment. For example, ḡCa can be decreased by substituting CaCl2 in the artificial sea water where the preparation is kept, by MgCl2. If the membrane potential initially oscillated, then this blockage abolishes the oscillations. This phenomenon is explained by a bifurcational diagram of the system (Figure 4). The diagram shows that the oscillations disappear via so-called supercritical Andronov–Hopf bifurcation (e.g., Rinzel and Ermentrout, 1989) when ḡCa decreases below some critical value.
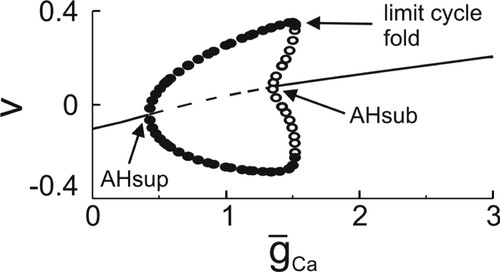
Figure 4. Bifurcation diagram for the Morris-Lecar model. Maximal and minimal values of the membrane potential V for different values ḡCa; ḡK=3. Solid line, stable steady state; dashed line, unstable steady state; filled circles, stable periodic oscillations; and open circles, unstable oscillations. AHsup, supercritical Andronov–Hopf bifurcation; AHsub, subcritical Andronov–Hopf bifurcation. The diagram is obtained by using XPPAUTO (Ermentrout, 2002).
Assessment and Future Directions
The MCN course proves the vitality of teaching advanced mathematics to life science students in a problem-driven way. A consequence of the approach is a shortage of time for expanded consideration of mathematical concepts. We addressed this problem by giving homework assignments that motivated further thinking on concepts and suggesting additional reading. One of the three weekly classes was a discussion session. We believe that it is very important to link the course content with ongoing research in the neurosciences. Accordingly, we have developed a number of homework assignments and tests motivated and closely related to influential publications.
We see the ultimate objective of the course in engaging students in using mathematical concepts in the neurosciences and developing their qualitative reasoning ability. In our experience, the engagement of biological students starts with their attempts to understand details of experiments. That was one of the reasons for us to choose neurobiological problems from the studies close to our own research interests. Finally, our experience suggests that methods of problem-based learning will help to achieve the main objectives of the course.
ACKNOWLEDGMENTS
We note that both Math 115/116 and MCN have been developed with support from the Emory College Center for Science Education. Mathematics and Computer Science Department personnel Michael Ferrara and Dr. Shanshuang Yang and HHMI Fellow Aron Barbey received a grant providing research funds to revise the Math 115/116 sequence and stipend support, respectively, from HHMI grant 52003727. A. O.'s development and first offerings of MCN were supported by HHMI grant 52005873. The principal investigator on both grants is Dr. Pat Marsteller, Director of Emory College Center for Science Education.