Active Learning Not Associated with Student Learning in a Random Sample of College Biology Courses
Abstract
Previous research has suggested that adding active learning to traditional college science lectures substantially improves student learning. However, this research predominantly studied courses taught by science education researchers, who are likely to have exceptional teaching expertise. The present study investigated introductory biology courses randomly selected from a list of prominent colleges and universities to include instructors representing a broader population. We examined the relationship between active learning and student learning in the subject area of natural selection. We found no association between student learning gains and the use of active-learning instruction. Although active learning has the potential to substantially improve student learning, this research suggests that active learning, as used by typical college biology instructors, is not associated with greater learning gains. We contend that most instructors lack the rich and nuanced understanding of teaching and learning that science education researchers have developed. Therefore, active learning as designed and implemented by typical college biology instructors may superficially resemble active learning used by education researchers, but lacks the constructivist elements necessary for improving learning.
INTRODUCTION
Students in introductory science courses often fail to learn fundamental scientific concepts (Halloun and Hestenes, 1985; McConnell et al., 2006). For example, students leaving introductory biology courses often believe evolution is caused by an animal's desire to change. Similarly, students often leave introductory physics courses believing heavy objects fall faster than lighter ones. There is a consensus among education researchers that much of the difficulty students have learning science can be attributed to the passive role students play during traditional lectures (McKeachie et al., 1990; Bonwell and Eison, 1991; Nelson, 2008). Therefore, in the past decade, there have been a growing number of calls to increase the amount of active learning in college science lectures (National Science Foundation [NSF], 1996; National Research Council [NRC], 1997, 2003, 2004; Boyer Commission on Educating Undergraduates in the Research University, 1998; Allen and Tanner, 2005; Handelsman et al., 2005).
Active learning is difficult to define, but essentially occurs when an instructor stops lecturing and students work on a question or task designed to help them understand a concept. A classic example of active learning is a think–pair–share discussion, in which students think about a question posed by the instructor, pair up with other students to discuss the question, and share answers with the entire class.
Extensive research shows that lectures using active learning can be much more effective than traditional lectures that use only direct instruction. For example, a seminal survey of introductory physics classes at nine high schools and 13 colleges and universities showed that, on average, students taught using active learning learned twice as much as students taught using direct instruction (Hake, 1998a,b). A host of quasi-experimental studies comparing student learning in a lecture-based course with student learning in an active-learning version of the course found that adding active learning increased student learning. These studies established that active learning could improve student learning across a wide variety of science disciplines (Ruiz-Primo et al., 2011), including biology (Jensen and Finley, 1996; Udovic et al., 2002; Knight and Wood, 2005; Freeman et al., 2007; Nehm and Reilly, 2007; Haak et al., 2011), physics (Shaffer and McDermott, 1992; Crouch and Mazur, 2001; Deslauriers et al., 2011), and chemistry (Wright, 1996; Naiz et al., 2002). There have been so many papers documenting this trend that it is now widely accepted that students taught with active learning will learn substantially more than students taught the same material with direct instruction.
However, a close review of the literature supporting the effectiveness of active learning reveals a serious limitation: Most of the active-learning courses studied to date were taught by instructors who had science education research experience. However, a close review of the literature supporting the effectiveness of active learning revels a serious limitation: Most of the active learning courses studied to date were taught by instructors who had science education research experience (e.g., Hake, 1998a,b; Knight and Wood, 2005; Deslauriers et al., 2011). By science education research, we mean they published papers on science education, received funding for education research, or attended conferences on science education research. We expect education researchers to have a rich and nuanced understanding of their field. This expertise may improve an instructor's effectiveness in many ways, including his or her ability to use active learning (Pollock and Finkelstein, 2008; Turpen and Finkelstein, 2009). This limitation has been recognized (Hake, 1998a; Pollock and Finkelstein, 2008), but the implications of this potential problem have not been explored. In particular, we are concerned the impressive learning gains documented in the active-learning literature may not be representative of what typical instructors are likely to obtain.
The goal of this research was to address that gap by studying the relationship between the use of active-learning instruction and how much students learned about natural selection in a random sample of introductory college biology courses from around the United States.
METHODS
Sample
The goal of our sampling design was to infer results to introductory biology courses at major colleges and universities throughout the United States. Thus, we began with a list of the two largest public colleges and universities from each of the 50 states, plus a list of the 50 top-ranked colleges and universities from the U.S. News & World Report Best Colleges 2009 ranking; some institutions were on both lists. From this combined list of 144 institutions, we randomly selected 77. We then contacted instructors at these institutions to ask them to participate during one of three consecutive semesters in 2009 and 2010.
In each school, we sought out introductory biology courses that taught natural selection and were designed for biology majors. To identify appropriate courses and course instructors, we used information gathered on institution websites and from biology department staff. We chose to survey courses teaching natural selection, because 1) it is a mechanism of evolution and therefore a core concept in biology (Gregory et al., 2011), 2) it is conceptually challenging for students to learn (Bishop and Anderson, 1990; Nehm and Reilly, 2007; Gregory, 2009), and 3) well-developed instruments exist to measure conceptual understanding of natural selection (e.g., Anderson et al., 2002; Nehm and Reilly, 2007; Nehm and Schonfeld, 2008). We contacted a total of 88 introductory biology instructors, sending at least three emails over the course of a month and following up with at least one phone call. We made a final attempt 4 to 6 mo later to contact instructors who did not respond to our initial queries.
Of the 88 instructors from 77 institutions we invited to participate in our study, 33 (38%) agreed to participate fully; these instructors are hereafter referred to as “fully participating instructors.” These instructors taught 29 different courses at 28 institutions in 22 states. Two of these institutions were private and 26 were public. Seven institutions were on the U.S. News & World Report Best Colleges 2009 list. If an instructor declined to participate in our study, we asked him or her to complete a survey describing his or her course and teaching methods so we could account for nonresponse bias. We were able to collect data from an additional 22 instructors, which represents 25% of the entire random sample of instructors and 44% of the instructors who did not agree to fully participate in this study. These instructors are hereafter referred to as “partially participating instructors.” Compared with previous research assessing the relationship between active-learning instruction and student learning gains, our sample is the largest sample of instructors and institutions and the only sample randomly selected from a broad population of college science instructors.
Assessing Learning
In each fully participating course, we assessed how much students learned about natural selection. We assessed learning by testing students near the beginning (pretest) and end (posttest) of the term, using two instruments that measure conceptual understanding of natural selection. First, we used the Conceptual Inventory of Natural Selection—Abbreviated (CINS-abbr), a 10-question, multiple-choice test (see sample questions in Supplemental Material 1; Anderson et al., 2002; Anderson, 2003; Fisher et al., unpublished data.). The questions on this instrument are nearly identical to those on an original concept inventory with well-established reliability (Anderson et al., 2002). Each distracter, or wrong answer, was designed to appeal to students who hold common misconceptions about natural selection. The content and face validity of these questions has been established for both the original CINS and the CINS-abbr (Anderson et al., 2002; Fisher et al., unpublished data.). Second, students completed one open-ended question from a set of five questions developed by Bishop and Anderson (1990) and later revised by Nehm and Reilly (2007) to measure college biology majors’ understanding of natural selection. This set of open-ended questions was designed to assess student understanding across different levels of Bloom's taxonomy (Nehm and Reilly, 2007). We used a question at Bloom's “application” level, which tests a student's ability to apply knowledge to a novel question. This set of questions tends to be more difficult for students than CINS questions (Nehm and Schonfeld, 2008). The question we used, hereafter called the “cheetah question,” was:
Cheetahs (large African cats) are able to run faster than 60 miles per hour when chasing prey. How would a biologist explain how the ability to run fast evolved in cheetahs, assuming their ancestors could run only 20 miles per hour?
To score student responses to the cheetah question, we developed, piloted, refined, and applied a coding rubric (Supplemental Material 2). Biology experts (T.M.A. and S.T.K.) designed the rubric after reviewing a rubric previously developed for the cheetah question (Nehm and Reilly, 2007). Our rubric gave more weight to three concepts we felt were core concepts a student must understand in order to understand natural selection: the existence of phenotypic variation within a population, the heritability of that variation, and differential reproductive success among individuals. We gave less weight to three additional concepts we felt were representative of more advanced understanding: the causes of variation, a change in the distribution of individual traits within a population, and change taking place over many generations. We designed this coding rubric to be sensitive to developing understanding, while allowing room for students to demonstrate more advanced understanding. To establish interrater reliability (IRR), two researchers (T.M.A. and C.A.C.) independently scored a random sample of 210 responses. IRR was measured using Pearson's correlation. There was a strong correlation between the total essay score awarded by the two researchers (r = 0.93, p < 0.0001). The researchers then independently scored the remaining responses to the cheetah question using the coding rubric.
Due to the large number of students included in this study (more than 8000), we scored a subsample of student responses to the cheetah question from each course. We randomly selected ∼50 students from each course and scored responses from students who completed both pre- and posttest cheetah questions. The mean subsample size was 42 students (SD = 12). For analyses of learning gains on the cheetah question described below, we excluded three courses whose subsample included fewer than 20 students and one course in which pre- and posttest responses could not be matched by student.
Students completed the CINS-abbr and the cheetah question on paper or online. To test for differences between student performance on paper versus performance using online instruments, we used independent samples t tests. We found no significant differences in mean test scores or learning gains between courses using online testing and those using paper testing (see full results in the Supplemental Material).
In some courses, students earned nominal course credit for logging into the online test, but actually completing test questions was voluntary in all classes. To look for differences between test performance in courses in which students earned credit and courses in which students did not, we again used independent samples t tests. We found only one significant difference between courses in which students earned credit and those in which students did not, and it was in the opposite direction than would be expected if awarding credit led to increased participation or performance. Students in courses in which credit was not awarded had significantly higher scores on the posttest CINS-abbr than students in courses that awarded credit (p = 0.03; see full results in the Supplemental Material). Because awarding credit was not associated with improved test performance or learning gains as would be predicted, we did not include this as a variable in further analysis.
Calculating Learning Gains
To decide how best to calculate how much students learned about natural selection, we examined the intercorrelations among pre- and posttest scores and four possible calculations of learning gains: effect size (Cohen's d), average normalized gain, percent change, and raw change (Table 1). The calculations of learning gains were highly intercorrelated (see the Supplemental Material), with Pearson's r ranging from 0.79–0.99 (all p values < 0.001; p was calculated using the Holm-Bonferonni method to account for error associated with multiple comparisons). Although average normalized gain is a commonly used estimator of learning gains in research on active learning (Hake, 1998a; Crouch and Mazur, 2001; Knight and Wood, 2005), it was strongly correlated with mean course pretest scores on the CINS-abbr (r = 0.51, p = 0.012; Supplemental Material). This correlation means that courses with high average pretest scores receive relatively higher normalized gains than courses with lower average pretest scores. Additionally, percent change was strongly negatively correlated with pretest scores on the cheetah question (r = –0.62, p = 0.003; Supplemental Material), resulting in a bias in the other direction. We ultimately chose to calculate learning gains using Cohen's d for a repeated measures design (Dunlap et al., 1996). No calculation of learning gains is without problems, so we also repeated the analyses described in Data Analysis, using each of the four calculations of learning gains. If all analyses produced similar results, we would feel confident that the way we chose to quantify student learning was not impacting our overall results.
| Learning gain calculation | Equation | Definition of variable |
|---|---|---|
| Effect size (Cohen's d for repeated measures)a | tp [2(1 – r)/(n)]1/2 | tp = t statistic from Student's paired t |
| r = correlation between pre/post | ||
| n = students completing pre/post | ||
| Average normalized gainb | (Post − Pre)/(10 − Pre)c | Post = mean course posttest score Pre = mean course pretest score |
| Percent change | (Post − Pre)/Pre | Post = mean course posttest score Pre = mean course pretest score |
| Raw change | Post − Pre | Post = mean course posttest score Pre = mean course pretest score |
Surveying Teaching Methods and Course Details
We gathered details on each course from the instructor and the students. An online survey (Supplemental Material 3) was used to gather data from fully participating instructors, as well as partially participating instructors. The instructor survey solicited information about the course, the instructor's teaching experience and teaching methods, and the students’ backgrounds. We also surveyed students during the posttest about their instructor's teaching methods and their perceptions of the course (Supplemental Material 4).
To corroborate self-report data from instructors, the instructor and his or her students answered an identical question about the instructor's use of active learning (Supplemental Material 3, question 8; Supplemental Material 4, question 3). Student reports of active learning agreed with instructor reports. Agreement between instructor responses and the most common student response (i.e., the mode) in each course was calculated using Cohen's kappa, which indicated substantial agreement (κ = 0.69; Viera and Garrett, 2005). Therefore, we used instructor reports of active learning for all further analyses.
Previous research has typically categorized instructors’ methods as either “active learning” or “traditional lectures,” but as active-learning methods have become more widely used, this categorization no longer adequately captures the variation among instructors’ teaching methods. We approached the problem of measuring an instructor's use of active learning by asking several questions and examining the relationships among instructor responses to these questions. We asked instructors three questions about their use of active learning in the lecture portion of their course. First, we asked instructors to report how often they used specific active-learning exercises (described in Table 2) previously shown to be effective (Ebert-May et al., 1997; Crouch and Mazur, 2001; Andrews et al., 2011; Deslauriers et al., 2011). We then created a continuous variable describing an instructor's weekly use of these active-learning exercises by summing the frequencies they reported for all six categories of exercises. To do so, we assumed each course met three times per week and counted “Once per week” as once per week, “Once per class” as three times per week, and “More than once per class” as six times per week. This variable may underestimate the use of active learning by excluding other exercises an instructor was using to promote active learning and by limiting “More than once per week” to only six exercises per week, so we also asked instructors to report their general use of any active learning by asking how often they used exercises meeting Hake's (1998a) definition of interactive engagement (another commonly used term for active learning):
activities designed at least in part to promote conceptual understanding through interactive engagement of students in heads-on (always) and hands-on (usually) activities which yield immediate feedback through discussion with peers and/or instructors.
| Exercise | More than once per class (%) | Once per class (%) | Once per week (%) | Never (or almost never) (%) |
|---|---|---|---|---|
| Activities in which students use data to answer questions while working in small groups | 5.7 | 2.9 | 34.3 | 57.1 |
| Student discussions in pairs or small groups to answer a question | 17.1 | 17.1 | 22.9 | 42.9 |
| Individual writing activities that require students to evaluate their own thinkinga | 0 | 3.1 | 28.1 | 68.8 |
| Clicker questions that test conceptual understanding | 34.3 | 11.4 | 5.7 | 48.6 |
| Classroom-wide interactions that require students to apply principles presented in class to a novel question | 8.6 | 20.0 | 37.1 | 34.3 |
| Other small group activities | 5.7 | 8.6 | 25.7 | 60.0 |
Finally, we asked instructors how many active-learning exercises they used during the section of the course dedicated to teaching natural selection. For all three questions, we described exercises instead of using common names (e.g., peer instruction, think–pair–share), so instructors would not have previous associations with the exercises described.
We found instructors’ reports of using specific active-learning exercises during the course were strongly correlated with their reports of using active learning in teaching natural selection (r = 0.52, p = 0.002). We therefore chose to use instructor reports about active learning use throughout the course for further analyses. In contrast to our expectations, instructors provided more conservative estimates of their general use of any active learning (as defined by Hake, 1998a) than their estimates of their use of specific active-learning exercises (Figure 1). For example, instructors who reported using general active-learning methods just once per week reported a mean of 3.33 specific exercises per week. Ultimately, we decided to quantify an instructor's use of active learning as the weekly frequency with which they used specific active-learning exercises, because this quantification allowed us to capture more variability among instructor methods. However, we also conducted statistical analyses with the more general report of active learning to assure results remained the same.
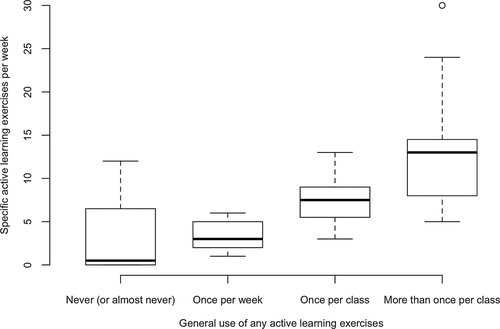
Figure 1. Comparison of instructor reports of their weekly use of specific active-learning exercises and instructor reports of their general use of active-learning exercises as defined by Hake (1998a). The line in the middle of the box represents the median weekly frequency of active-learning use for instructors in the group. The top of the box represents data points in the 75th percentile and the bottom of the box represents data points in the 25th percentile. The space within the box is called the interquartile range (IQR). Whiskers represent the lowest and highest data points no more than 1.5 times the IQR above and below the box. Data points not included in this range are represented as circles.
Data Analysis
We used data gathered from the instructor survey to compare fully participating instructors with partially participating instructors to check for selection bias resulting from nonresponse. We looked for differences using independent samples t tests and Fisher's exact tests. We found no differences between the two groups of instructors, suggesting nonresponse did not cause a selection bias. There were no significant differences in the mean number of specific active-learning exercises used per week, mean class size, mean teaching experience, mean class time dedicated to teaching natural selection, or mean attendance rates. Neither were there differences in type of institution (public or private), the list their institution came from (large public institutions or most prestigious institutions), the instructor's position, or the frequency with which they used general active-learning methods (see full results in the Supplemental Material).
To answer our question of interest—is active-learning instruction positively associated with student learning gains in typical college biology courses?—we used general linear regression models. We used one model with effect size of learning on the CINS-abbr as the response variable and one model with effect size of learning on the cheetah question as the response variable. We used two models, because four courses had insufficient data to analyze learning gains on the cheetah question, but had complete CINS-abbr data. Using two models allowed us to avoid unnecessarily excluding these courses from all analyses. Additionally, we examined linear regression models using other calculations of learning gains, as well as a model that replaced the continuous weekly frequency of specific active-learning exercises with the more general categorical use of any active learning, to see if results remained the same. We checked assumptions for our models using QQ plots and plots of fitted values versus residuals. Assumptions were met for all linear regression models.
Many factors affect how much students learn in a course, so we used data gathered from the instructor survey and student survey to control for variation in learning gains due to factors other than the use of active learning. We included several continuous control variables in our linear models, including the number of years an instructor had taught college biology, hours of class time devoted to teaching natural selection, proportion of students who attended class regularly, proportion of students who completed both the pre- and posttest, and class size. Student responses to questions about how difficult they found the course compared with previous science courses and how interesting they found the course were coded numerically and also included as continuous control variables. Students chose from a Likert scale (Supplemental Material 4), which we then coded from one to five, where one corresponded to “Very uninteresting” and “Much less difficult” and five corresponded to “Very interesting” and “Much more difficult.” We then calculated means for each course.
We used indicator variables to include categorical control variables in our models. We included a factor accounting for the presence or absence of nonmajors in a course. We also included a two-level factor for the instructor's position: tenure track or non-tenure track. Last, we included two factors to describe whether the instructor addressed common student misconceptions about natural selection: one for whether or not an instructor reported “explaining to students why misconceptions are incorrect” and a second for whether or not an instructor reported “using active-learning exercises and otherwise making a substantial effort toward correcting misconceptions.”
We excluded data from one question on the instructor survey that was strongly intercorrelated with two other control variables. The number of times an instructor had taught the course was correlated with both the number of years an instructor had taught college biology (r = 0.50, p = 0.002) and class size (r = 0.49, p = 0.004). Therefore, we excluded the number of times an instructor had taught the course from our models.
RESULTS
Our analysis produced four noteworthy results. First, instructors reported frequently using active-learning exercises (Table 2). Thirty-nine percent (n = 13) of instructors reported using four or more different activities (as described in Table 2) on a weekly basis and only 6% (n = 2) reported using none of these activities. Instructors reported using a mean of 8.03 (SD = 6.65) exercises per week, which would be equivalent to about three clicker questions per class meeting. During the portion of the course dedicated to teaching natural selection, instructors reported using a mean of 2.88 (SD = 1.43) active-learning exercises. When asked to categorize the frequency with which they used general active-learning methods as defined by Hake (1998a), 61% of instructors reported using active learning at least once per class meeting (Table 3). Introductory biology instructors’ reports of their use of active learning in this study were similar to physics instructors’ reports of their use of research-based teaching methods (most of which incorporate active learning); in a national survey of college physics courses, 48.1% of instructors reported they currently used at least one research-based method and 34.4% reported using two or more (Henderson and Dancy, 2009).
| Frequency | Number of instructors | Percent of instructors |
|---|---|---|
| More than once per class | 12 | 36.4 |
| Once per class | 8 | 24.2 |
| Once per week | 9 | 27.3 |
| Never (or almost never) | 4 | 12.1 |
Our second noteworthy result was that learning gains in many of the courses were modest (Table 4). Effect sizes (Cohen's d) on the CINS-abbr ranged from −0.11–1.26 and the mean effect size was 0.49 (SD = 0.31). Thirty-nine percent (n = 13) of courses had an effect size lower than 0.42, which corresponds to students answering only one more question (out of 10) correctly on the posttest than on the pretest.1 When learning was calculated as average normalized gain, the mean gain was 0.26 (SD = 0.17). On the cheetah question, learning gains were even lower. Effect sizes ranged from −0.16–0.58. The mean effect size was 0.15 (SD = 0.19) and the mean normalized gain for the cheetah question was 0.06 (SD = 0.08). These remarkably low learning gains suggest students are not learning to apply evolutionary knowledge to novel questions in introductory biology courses.
Our third and most important result was that we did not find an association between the weekly frequency of active-learning exercises used in introductory biology courses and how much students learned about natural selection (Figure 2 and Table 5). An instructor's use of active learning was not associated with learning gains on the CINS-abbr (p = 0.058) or the cheetah question (p = 0.669), and the regression coefficients for active learning in both models were negative, although not statistically significant (Table 5). When we calculated learning gains as average normalized gain, percent change, or raw change, we obtained the same result (Figure 3 and Table 6; Supplemental Material). When we replaced the weekly frequency of specific active-learning exercises with an instructor's more general use of any active-learning methods, we again obtained the same result. No matter how we quantified these variables, or what control variables we included in the analysis, we obtained the same result: Student learning was not positively related to how much active learning instructors used.
| Test | Minimum | Maximum | Mean | SD |
|---|---|---|---|---|
| CINS-abbr pretesta | 3.56 | 7.57 | 5.38 | 0.86 |
| CINS-abbr posttestb | 4.29 | 8.80 | 6.52 | 1.20 |
| Cheetah pretest | 1.08 | 4.83 | 2.92 | 0.83 |
| Cheetah posttest | 1.50 | 4.90 | 3.22 | 0.85 |
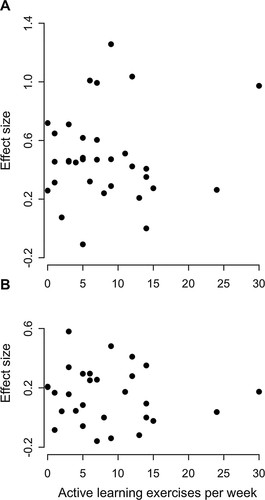
Figure 2. Relationship between learning gains (Cohen's d) and the number of active-learning exercises an instructor used per week. The number of active-learning exercises per week was calculated by summing the number of times per week instructors reported using all of the exercises described in Table 2. (A) Learning gains on the CINS-abbr (n = 33). (B) Learning gains on the cheetah question (n = 29).
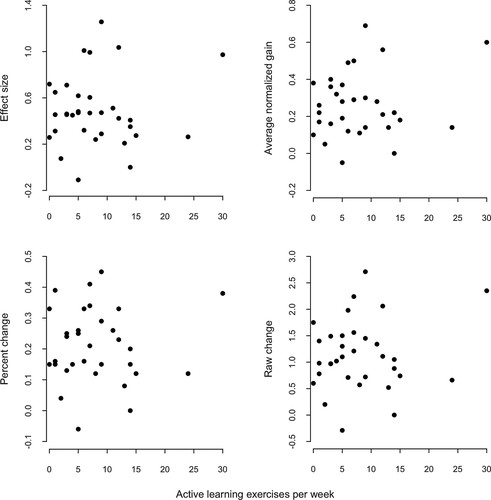
Figure 3. Relationship between four different calculations of learning gains on the CINS-abbr and the number of active-learning exercises an instructor used per week. The CINS-abbr was scored out of 10 points, so a raw change of one is equivalent to earning one more point on the posttest than on the pretest. Overall, these graphs are very similar; there is no evidence of a positive relationship between learning gains and the use of active-learning instruction, no matter how we calculate learning gains.
| Regression coefficient [95% confidence interval] | ||
|---|---|---|
| Linear model variable | CINS-abbr posttest and CINS-abbr pretest model | Cheetah question model |
| Intercept | −1.88 [−2.16, −1.62]* | 0.098 [−1.729, 1.924] |
| Weekly active learning | −0.02 [−0.04, 0.00] | −0.000 [−0.024, 0.016] |
| Instructor position (tenure track) | −0.10 [−0.33, 0.13] | 0.168 [−0.078, 0.414] |
| Students regularly attending (%) | −0.03 [−0.97, 0.91] | −0.459 [−1.740, 0.821] |
| Hours spent on natural selection | 0.00 [−0.03, 0.03] | −0.011 [−0.036, 0.014] |
| Class size | 0.00 [−0.00, 0.00]e | 0.000 [−0.000, 0.000]e |
| Years of teaching experience | 0.00 [−0.01, 0.01] | −0.005 [−0.014, 0.003] |
| Students pre/posttest (%) | 0.06 [−0.47, 0.60] | 0.298 [−0.263, 0.860] |
| Misconceptions (explained)a | 0.23 [0.01, 0.45]* | 0.194 [−0.036, 0.423] |
| Misconceptions (active learning and otherwise)b | 0.25 [0.00, 0.50]* | −0.019 [−0.265, 0.227] |
| Course difficulty (student-rated)c | 0.29 [0.20, 0.57]* | −0.003 [−0.292, 0.286] |
| Student interest in course | 0.33 [0.06, 0.60]* | 0.058 [−0.237, 0.352] |
| Nonmajors (absent)d | 0.37 [−0.04, 0.77] | 0.447 [−0.109, 1.004] |
| Linear model coefficient | Effect size | Average normalized gain | Percent change | Raw change |
|---|---|---|---|---|
| Intercept | −* | −* | − | − |
| Weekly active learning | − | − | − | − |
| Instructor position (tenure track) | − | − | + | − |
| Students regularly attending (%) | − | + | − | − |
| Hours spent on natural selection | − | − | + | + |
| Class size | − | − | + | − |
| Years of teaching experience | + | + | − | + |
| Students pre/posttest (%) | + | + | + | + |
| Misconceptions (explained)a | +* | + | +* | + |
| Misconceptions (active learning otherwise)b | +* | + | + | + |
| Course difficulty (student-rated)c | +* | +* | + | + |
| Student interest in course | +* | + | +* | +* |
| Nonmajors (absent)d | + | + | +* | + |
Despite the absence of a positive relationship between active learning and student outcomes, our final noteworthy result is that several variables were positively related to student learning measured by the CINS-abbr (Table 5). Our analysis revealed the two misconception factors (“explaining why misconceptions are incorrect” and “using active-learning exercises to make a substantial effort toward changing misconceptions”) were positively associated with learning gains on the CINS-abbr (p = 0.045 and p = 0.048, respectively). This finding corroborates previous papers suggesting that misconceptions must be confronted before students can learn natural selection (Sinatra et al., 2008; Kalinowski et al., 2010). Because common misconceptions are used as distracters in CINS-abbr questions, we would expect courses in which misconceptions were directly targeted to have higher learning gains on this instrument. That said, misconceptions seem to be the largest barrier to understanding that students face when learning natural selection (Bishop and Anderson, 1990; Gregory, 2009), so a test that measures the extent to which students reject misconceptions is likely to be a reliable measure of their overall understanding (Nehm and Schonfeld, 2008). Further research will be necessary to determine the relationship between how students learn natural selection and how an instructor addresses common misconceptions about natural selection.
In addition to the misconception factors, how difficult students found a course relative to past science courses and how interesting students found a course were also significantly positively associated with student learning on the CINS-abbr (p = 0.040 and p = 0.021, respectively). The questions used to gather student perception data provide insufficient detail to understand the complex relationships among instructor behavior, student perceptions, and student learning. Nevertheless, these results suggest research that examines student learning should not overlook the impact of students’ experiences in a course.
DISCUSSION
We have shown that even though instructors of introductory college biology courses are using active learning, students in many of their courses have learned very little about natural selection. Notably, students in most courses were no more successful in applying their knowledge of natural selection to a novel question at the end of the course than they were at the beginning of the course. The absence of a relationship between active learning and student learning is in stark contrast to a large body of research supporting the effectiveness of active learning. We attribute this contrast to the fact that we studied a different population of instructors. We randomly sampled college biology faculty from a list of major universities. Therefore, instructors using active learning in our study represent the range of science education expertise among introductory college biology instructors using these methods. In contrast, most of the faculty using active learning in previous studies had backgrounds in science education research. The expertise gained during research likely prepares these instructors to use active learning more effectively (Pollock and Finkelstein, 2008; Turpen and Finkelstein, 2009).
Specifically, it is possible that a thorough understanding of, commitment to, and ability to execute a constructivist approach to teaching are required to successfully use active learning (NRC, 2000). Constructivism—the theory that students construct their own knowledge by incorporating new ideas into an existing framework—likely permeates all aspects of education researchers’ instruction, including how they use active learning. Without this expertise, the active-learning exercises an instructor uses may have superficial similarities to exercises described in the literature, but may lack constructivist elements necessary for improving learning (NRC, 2000). For example, our results suggest that addressing common student misconceptions may lead to higher learning gains. Constructivist theory argues that individuals construct new understanding based on what they already know and believe (Piaget, 1973; Vygotsky, 1978; NRC, 2000), and what students know and believe at the beginning of a course is often scientifically inaccurate (Halloun and Hestenes, 1985; Bishop and Anderson, 1990; Gregory, 2009). Therefore, constructivist theory argues that we can expect students to retain serious misconceptions if instruction is not specifically designed to elicit and address the prior knowledge students bring to class.
A failure to address misconceptions is just one example of how active-learning instruction may fall short. Instructors may fail to achieve the potential of active learning in the design or implementation of exercises, or both. There are many possible ways that active-learning exercises could be poorly designed. For example, questions used in an exercise may only require students to recall information, when higher-order cognitive processing (e.g., application) is required to fully grasp scientific concepts (Crowe et al., 2008). Alternatively, questions posed to students could be poorly connected to other material in the course, such that students fail to see important relationships among concepts (NRC, 2000). It is also possible that the active-learning exercises used to discuss fundamental theories may not be sufficiently interesting to students to motivate them to participate (Boekaerts, 2001).
On the other hand, regardless of how well an active-learning exercise is designed, an instructor must make many implementation decisions that will ultimately affect the success of the exercise. For example, a think–pair–share discussion may not be effective if the instructor does not allow students enough time to think about a question (Allen and Tanner, 2002). Or, an instructor may solicit only one answer from the class and therefore fail to expose the range of ideas held by students. In addition, an instructor may not ask students to predict the outcome of a demonstration or thought experiment and therefore fail to make students aware of their own erroneous ideas (Crouch et al., 2004). Furthermore, instructors may display any number of subtle behaviors or attitudes that influence the extent to which students participate in active-learning exercises, and thereby affect how much students learn (Turpen and Finkelstein, 2009, 2010).
Our results corroborate research showing that college science teachers are incorporating active-learning methods but are often doing so ineffectively. A recent study compared college biology instructor's self-reports of teaching with expert observations of the instructor's teaching and found that the instructors felt they were using reform methods, but experts did not confirm this (Ebert-May et al., 2011). Similarly, a national survey of teaching practices in college physics courses found that 63.5% of instructors reported using think–pair–share discussions, but 83% of the instructors who used this method did not use it as suggested by researchers (Henderson and Dancy, 2009). Mounting evidence suggests that somewhere in the communication between science education researchers and typical college science instructors, elements of evidence-based methods and curricula crucial to student learning are lost.
The results of this study have three implications for education researchers across science disciplines. First, we need to build a better understanding of what makes active-learning exercises effective by rigorously exploring which elements are necessary and sufficient to improve learning (e.g., see Crouch et al., 2004; Smith et al., 2009, 2011; Perez et al., 2010). Second, we need to develop active-learning exercises useful for a broad population of instructors. Third, we need to identify what training and ongoing support the general population of college science faculty and future faculty need to be able to effectively use active learning, taking into account obstacles instructors will face, including individual, situational, and institutional barriers to reform (Henderson, 2005; Henderson and Dancy, 2007, 2008).
Our results also have two important implications for instructors. First, no one can assume that they are teaching effectively just because they are using active learning. Therefore, instructors need to carefully assess the effectiveness of their instruction to determine whether active learning is reaching its potential. There are a growing number of reliable and valid multiple-choice and essay tests that assess student knowledge (Anderson et al., 2002; Baum et al., 2005; Nehm and Reilly, 2007; Smith et al., 2008; Nadelson and Southerland, 2009). We recommend using these tests in a pre/posttest design to assess the effectiveness of instruction, as well as using formative assessments to monitor learning throughout instruction (Angelo and Cross, 1993; Marrs and Novak, 2004). Second, instructors should assume students enter science courses with preexisting ideas that impede learning and that are unlikely to change without instruction designed specifically for that purpose (NRC, 2000). To replace students’ misconceptions with a scientifically accepted view of the world, instructors need to elicit misconceptions, create situations that challenge misconceptions, and emphasize conceptual frameworks, rather than isolated facts (Hewson et al., 1998; Tanner and Allen, 2005; Kalinowski et al., 2010).
Our study revealed that active learning was not associated with student learning in a broad population of introductory college biology courses. These results imply active learning is not a quick or easy fix for the current deficiencies in undergraduate science education. Simply adding clicker questions or a class discussion to a lecture is unlikely to lead to large learning gains. Effectively using active learning requires skills, expertise, and classroom norms that are fundamentally different from those used in traditional lectures. Appreciably improving student learning in college science courses throughout the United States will likely require reforming the way we prepare and support instructors and the way we assess student learning in our classrooms.
FOOTNOTES
1 A course average was calculated as the average number of points (out of 10) scored on the pre- or posttest CINS-abbr. An effect size can be calculated as the change in average score (Post − Pre) divided by a pooled SD. The average pooled SD for the CINS-abbr was 2.39. We divided the change in average score that interested us (a one-point increase between pre- and posttest course averages) by the average pooled SD for our sample. That calculation produced the effect size corresponding to students across courses answering, on average, one more question correctly on the posttest CINS-abbr than they answered correctly on the pretest.
ACKNOWLEDGMENTS
Support for this study was provided by NSF-CCLI 0942109. We thank the instructors and course coordinators who dedicated time to this study: Theresa Theodose, Heather Henter, Brian Perry, Carla Hass, Alan L. Baker, Clyde Herreid, Norris Armstrong, Farahad Dastoor, Michael R. Tansey, Denise Woodward, Kristen Porter-Utley, Leana Topper, Susan Piscopo, Rogene Schnell, Brent Ewers, John Longino, Waheeda Khalfan, Denise Kind, Scott Freeman, Jon Sandridge, Rebekka Darner, Peter Houlihan, Jacob Krans, Wyatt Cross, Peter Dunn, Don Waller, Scott Solomon, Benjamin Normark, Jason Flores, Teena Michael, Drew Joseph, Dmitri Petrov, Dustin Rubenstein, and others who wish to remain anonymous. We also thank the students in participating courses. Finally, we thank Tatiana Butler, Megan Higgs, Scott Freeman, and two anonymous reviewers for assistance with research, analysis, and manuscript revision. This research was exempt from the requirement of review by the Institutional Review Board, no. SK082509-EX.