The Other Half of the Story: Effect Size Analysis in Quantitative Research
Abstract
Statistical significance testing is the cornerstone of quantitative research, but studies that fail to report measures of effect size are potentially missing a robust part of the analysis. We provide a rationale for why effect size measures should be included in quantitative discipline-based education research. Examples from both biological and educational research demonstrate the utility of effect size for evaluating practical significance. We also provide details about some effect size indices that are paired with common statistical significance tests used in educational research and offer general suggestions for interpreting effect size measures. Finally, we discuss some inherent limitations of effect size measures and provide further recommendations about reporting confidence intervals.
INTRODUCTION
Quantitative research in biology education is primarily focused on describing relationships between variables. Authors often rely heavily on analyses that determine whether the observed effect is real or attributable to chance, that is, the statistical significance, without fully considering the strength of the relationship between those variables (Osbourne, 2008). While most researchers would agree that determining the practical significance of their results is important, statistical significance testing alone may not provide all information about the magnitude of the effect or whether the relationship between variables is meaningful (Vaske, 2002; Nakagawa and Cuthill, 2007; Ferguson, 2009).
In education research, statistical significance testing has received valid criticisms, primarily because the numerical outcome of the test is often promoted while the equally important issue of practical significance is ignored (Fan, 2001; Kotrlik and Williams, 2003). As a consequence, complete reliance on statistical significance testing limits understanding and applicability of research findings in education practice. Therefore, authors and referees are increasingly calling for the use of statistical tools that supplement traditionally performed tests for statistical significance (e.g., Thompson, 1996; Wilkinson and American Psychological Association [APA] Task Force on Statistical Inference, 1999). One such tool is the confidence interval, which provides an estimate of the magnitude of the effect and quantifies the uncertainly around this estimate. A similarly useful statistical tool is the effect size, which measures the strength of a treatment response or relationship between variables. By quantifying the magnitude of the difference between groups or the relationship among variables, effect size provides a scale-free measure that reflects the practical meaningfulness of the difference or the relationship among variables (Coe, 2002; Hojat and Xu, 2004).
In this essay, we explain the utility of including effect size in quantitative analyses in educational research and provide details about effect size metrics that pair well with the most common statistical significance tests. It is important to note that effect size and statistical significance testing (which we will shorten to “significance testing,” also known as hypothesis testing) are complementary analyses, and both should be considered when evaluating quantitative research findings (Fan, 2001). To illustrate this point, we begin with two hypothetical examples: one in biology and one in education.
Effect Size and Statistical Significance Testing: Why Both Are Necessary
Imagine that a researcher set up two treatment conditions: for example, unfertilized and fertilized plants in a greenhouse or, similarly, reformed and traditional teaching approaches in different sections of an introductory biology course. The researcher is interested in knowing whether the first treatment is more or less effective than the second, using some measurable outcome (e.g., dried plant biomass or student performance on an exam); this constitutes the research hypothesis. The null hypothesis states that there is no difference between the treatments. Owing to sampling variation in a finite sample size, even if the two treatments are equally effective (i.e., the null hypothesis is true), one sample mean will nearly always be greater than the other. Therefore, the researcher must employ a statistical significance test to determine the probability of a difference between the sample means occurring by chance when the null hypothesis is true. Using the appropriate test, the researcher may determine that sampling variability is not a likely explanation for the observed difference and may reject the null hypothesis in favor of the alternative research hypothesis. The ability to make this determination is afforded by the statistical power, which is the probability of detecting a treatment effect when one exists, of the significance test. Statistical power is primarily determined by the size of the effect and the size of the sample: as either or both increase, the significance test is said to have greater statistical power to reject the null hypothesis.
The basis for rejection of the null hypothesis is provided by the p value, which is the output of statistical significance testing that is upheld as nearly sacred by many quantitative researchers. The p value represents the probability of the observed data (or more extreme data) given that the null hypothesis is true: Pr(observed data|H0), assuming that the sampling was random and done without error (Kirk, 1996; Johnson, 1999). A low value of p, typically below 0.05, usually leads researchers to reject the null hypothesis. However, as critics of significance testing have pointed out, the abuse of this rather arbitrary cutoff point tends to reduce the decision to a reject/do not reject dichotomy (Kirk, 1996). In addition, many researchers believe that the smaller the value of p, the larger the treatment effect (Nickerson, 2000), equating the outcome of significance testing to the importance of the findings (Thompson, 1993). This misunderstanding is likely due to the fact that when sample size is held constant, the value of p correlates with effect size for some statistical significance tests. However, that relationship completely breaks down when sample size changes. As described earlier, the ability of any significance test to detect a fixed effect depends entirely on the statistical power afforded by the size of the sample. Thus, for a set difference between two populations, simply increasing sample size may allow for easier rejection of the null hypothesis. Therefore, given enough observations to afford sufficient statistical power, any small difference between groups can be shown to be “significant” using a statistical significance test.
The sensitivity of significance testing to sample size is an important reason why many researchers advocate reporting effect sizes and confidence intervals alongside test statistics and p values (Kirk, 1996; Thompson, 1996; Fan, 2001). Kotrlik and Williams (2003) highlight a particularly clear example in which statistical and practical significance differ. In their study, Williams (2003) was interested in comparing the percent time that faculty members spend teaching with the percent time that they would prefer to spend teaching. Despite the fact that the mean differences between actual and preferred teaching time were statistically significant (t154 = 2.20, p = 0.03), the effect size (Cohen's d = 0.09) was extremely small (see Tables 1 and 2 for effect size metrics and interpretations). As a result, the author did not suggest that there were practically important differences between actual and preferred teaching time commitments (Williams, 2003). Reporting the confidence interval would have also illustrated the small effect in this study: while the confidence interval would not have contained zero, one of its end points would have been very close to zero, suggesting that the population mean difference could be quite small.
 |
| Effect size measure | Small effect size | Medium effect size | Large effect size | Very large effect size |
|---|---|---|---|---|
| Odds ratio | 1.5 | 2.5 | 4 | 10 |
| Cohen's d (or one of its variants) | 0.20 | 0.50 | 0.80 | 1.30 |
| r | 0.10 | 0.30 | 0.50 | 0.70 |
| Cohen's f | 0.10 | 0.25 | 0.40 | — |
| Eta-squared | 0.01 | 0.06 | 0.14 | — |
Although Williams (2003) presents a case in which a small “significant” p value could have led to an erroneous conclusion of practically meaningful difference, the converse also occurs. For example, Thomas and Juanes (1996) present an example from a study of juvenile rainbow trout willingness to forage under the risk of predation (Johnsson, 1993). An important part of the study tested the null hypothesis that large and small juveniles do not differ in their susceptibility to the predator, an adult trout. Using eight replicate survivorship trials, Johnsson (1993) found no significant difference in the distribution of risk between the two size classes (Wilcoxon signed-rank test: T+ = 29, p = 0.15). However, the data suggest that there may in fact be a biologically significant effect: on average, 19 ± 4.9% (mean ± SE) of the large fish and 45 ± 7% of the small fish were killed by the predator (Johnsson, 1993). This difference likely represents a medium effect size (see Table 2; Thomas and Juanes, 1996). Not reporting effect size resulted in the researchers failing to reject the null hypothesis, possibly due to low statistical power (small sample size), and the potential to erroneously conclude that there were no differences in relative predation risk between size classes of juvenile trout.
Thus, metrics of effect size and statistical significance provide complementary information: the effect size indicates the magnitude of the observed effect or relationship between variables, whereas the significance test indicates the likelihood that the effect or relationship is due to chance. Therefore, interpretations derived from statistical significance testing alone have the potential to be flawed, and inclusion of effect size reporting is essential to inform researchers about whether their findings are practically meaningful or important. Despite the fact that effect size metrics have been available since the 1960s (Huberty, 2002) and have been recognized as being a potentially useful aspect of analyses since the 1990s (e.g., Cohen, 1994; Thompson, 1996; Wilkinson and APA Task Force on Statistical Inference, 1999), the adoption of effect size as a complement to significance testing has been a slow process, even in high-impact research (Tressoldi et al., 2013). Nevertheless, many journals are beginning to develop editorial policies requiring some measure of effect size to be reported in quantitative studies (e.g., Royer, 2000). In response to this need for implementation, we next discuss the various methods used to calculate effect sizes and provide guidance regarding the interpretation of effect size indices.
Measures of Effect Size: Two Categories
We concentrate on parametric tests and group effect sizes into two main categories: those for 1) comparing two or more groups and 2) determining strength of associations between variables. The most frequently used statistical tests in these two categories are associated with specific effect size indices (see Table 1; Cohen, 1992), and we will discuss some of the more common methods used for each below. Refer to Figure 1 for a general guide to selecting the appropriate effect size measure for your data.
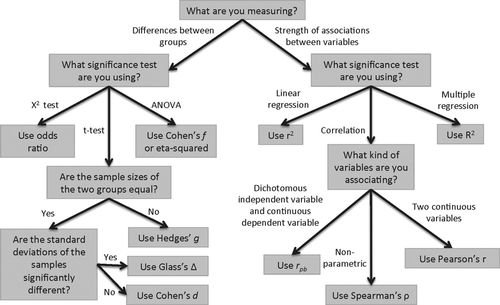
Figure 1. A dichotomous key to selecting an appropriate measure of effect size. Because many quantitative researchers are already accustomed to employing statistical significance tests but may want to begin reporting effect sizes as well, we suggest effect size metrics that are appropriate for data analyzed using common significance tests. Although not intended to be a comprehensive guide to effect size indices, this key indicates many of the measures relevant for common quantitative analyses in educational research. Researchers are encouraged to gather more information about these metrics, including their assumptions and limitations.
Comparing Two or More Groups.
A common approach to both biological and educational research questions is to compare two or more groups, such as in our earlier examples comparing the effects of a treatment on plant growth or student performance. For these kinds of analyses, the appropriate measure of effect size will depend on the type of data collected and the type of statistical test used. We present here a sample of effect size metrics relevant to χ2, t, or F tests.
When comparing the distribution of a dichotomous variable between two groups, for instance, when using a χ2 test of homogeneity, the odds ratio is a useful effect size measure that describes the likelihood of an outcome occurring in the treatment group compared with the likelihood of the outcome occurring in the control group (see Table 1; Cohen, 1994; Thompson, 1996). An odds ratio equal to 1 means that the odds of the outcome occurring is the same in the control and treatment groups. An odds ratio of 2 indicates that the outcome is two times more likely to occur in the treatment group when compared with the control group. Likewise, an odds ratio of 0.5 indicates that the outcome is two times less likely to occur in the treatment group when compared with the control group. Granger et al. (2012) provide an example of reporting odds ratios in educational research. In their study, the effectiveness of a new student-centered curriculum and aligned teacher professional development was compared with a control group. One of the instruments used to measure student outcomes produced dichotomous data, and the odds ratio provided a means for reporting the treatment's effect size on this student outcome. However, the odds ratio alone does not quantify treatment effect, as the magnitude of the effect depends not only on the odds ratio but also on the underlying value of one of the odds in the ratio. For example, if a new treatment for an advanced cancer increases the odds of survival by 50% compared with the existing treatment, then the odds ratio of survival is 1.5. However, if oddscontrol = 0.002 and oddstreatment = 0.003, the increase is most likely not practically meaningful. On the other hand, if an oddscontrol = 0.5 and the oddstreatment = 0.75, this could be interpreted as a substantial increase that one might find practically meaningful.
When comparing means of continuous variables between two groups using a t test, Cohen's d is a useful effect size measure that describes the difference between the means normalized to the pooled standard deviation (SD) of the two groups (see Table 1; Cohen, 1988). This measure can be used only when the SDs of two populations represented by the two groups are the same, and the population distributions are close to normal. If the sample sizes between the two groups differ significantly, Hedges’ g is a variation of Cohen's d that can be used to weight the pooled SD based on sample sizes (see Table 1 for calculation; Hedges, 1981). If the SDs of the populations differ, then pooling the sample SDs is not appropriate, and other ways to normalize the mean difference should be used. Glass's Δ normalizes the difference between two means to the SD of the control sample (see Table 1). This method assumes that the control group's SD is most similar to the population SD, because no treatment is applied (Glass et al., 1981). There are many relevant examples in the educational research literature that employ variations on Cohen's d to report effect sizes. Abraham et al. (2012) used Cohen's d to show how an instructional treatment affected students’ post scores on a test of the acceptance of evolutionary theory. Similarly, Matthews et al. (2010) used Cohen's d to show the magnitude of change in student's beliefs about the role of mathematics in biology due to changes in course materials, delivery, and assessment between different years of the same course. Gottesman and Hoskins (2013) applied Cohen's d to compare pre/post means of data collected using an instrument measuring students’ critical thinking, experimental design ability, attitudes, and beliefs.
When comparing means of three or more groups, for instance, when using an analysis of variance (ANOVA) test, Cohen's f is an appropriate effect size measure to report (Cohen, 1988). In this method, the sum of the deviations of the sample means from the combined sample mean is normalized to the combined sample SD (see Table 1). Note that this test does not distinguish which means differ, but rather just determines whether all means are the same. Other effect size measures commonly reported with ANOVA, multivariate analysis of covariance (MANCOVA), and analysis of covariance (ANCOVA) results are eta-squared and partial eta-squared. Eta-squared is calculated as the ratio of the between-groups sum of squares to the total sum of squares (see Table 1; Kerlinger, 1964). Alternatively, partial eta-squared is calculated as the ratio of the between-groups sum of squares to the sum of the between-groups sum of squares and the error sum of squares (Cohen, 1973). For example, Quitadamo and Kurtz (2007) reported partial eta-squared, along with ANCOVA/MANCOVA results, to show effect sizes of a writing treatment on student critical thinking. However, eta-squared is deemed by some as a better measure to report, because it describes the variance accounted for by the dependent measure (Levine and Hullett, 2002), which bears similarities to typical measures reported in correlational studies.
Determining Strength of Association between Variables.
Another common approach in both biological and educational research is to measure the strength of association between two or more variables, such as determining the factors that predict student performance on an exam. Many researchers using this type of analysis already report appropriate measures of effect size, perhaps without even realizing they are doing so. In most cases, the regression coefficient or analogous index provides information regarding the magnitude of the effect.
The Pearson product-moment correlation coefficient (Pearson's r) measures the association between two continuous variables, such as in a linear regression (see Table 1). Squaring the r value when performing a simple linear regression results in the coefficient of determination (r2), a measure that provides information about the amount of variance shared between the two variables. For multiple-regression analysis, the coefficient of multiple determination (R2) is an appropriate effect size metric to report. If one of the study variables is dichotomous, for example, male versus female or pass versus fail, then the point-biserial correlation coefficient (rpb) is the appropriate metric of effect size. The point-biserial correlation coefficient is similar in nature to Pearson's r (see Table 1). An easy-to-use Web-based calculator to calculate rpb is located at www.vassarstats.net/pbcorr.html. Spearman's rank correlation coefficient (ρ) is a nonparametric association measure that can be used when both variables are measured on an ordinal or ranked scale or when variables on a continuous scale are not normally distributed. This measure can be used only after one applies a transformation to the data that ranks the values. Because this is a nonparametric measure, Spearman's ρ is not as sensitive to outliers as Pearson's r. Note that there are also variations of Spearman's ρ that handle different formats of data. Most statistical software packages can calculate all of these measures of variable association, as well as most of the measures comparing differences between groups. However, one must be careful to be sure that values provided by the software are indeed what they are claimed to be (Levine and Hullett, 2002).
How to Interpret Effect Sizes
Once you have calculated the effect size measure, how do you interpret the results? With Cohen's d and its variants, mean differences are normalized to SD units. This indicates that a d value of 0.5 can be interpreted as the group means differing by 0.5 SDs. Measures of association report the strength of the relationship between the independent and dependent variables. Additional manipulation of these association values, for example, r2, can tell us the amount of shared variance between the variables. For the case of regression analysis, we can assume that an r2 value of 0.3 means that 30% of the variance in the dependent variable can be explained by the independent variable. Additionally, McGraw and Wong (1992) developed a measure to report what they call “the common language effect size indicator,” which describes the probability that a random value sampled from one group will be greater than a random value sampled from a comparison group (McGraw and Wong, 1992).
Statisticians have determined qualitative descriptors for specific values of each type of effect size measure (Cohen, 1988, 1992; Rosenthal, 1996). For more interpretation of these types of measures, see Table 2. These values can help guide a researcher to make some sort of statement about the qualitative nature of the effect size, which is useful for communicating the meaning of results. Additionally, effect size interpretations impact the use of data in meta-analyses. Please refer to Box 1 to see an example of how interpretations of the different types of effect size measures can be converted from one type to another for the purpose of meta-analysis.
Effect size measures are an important tool used when performing meta-analyses because they provide a standardized method for comparing results across different studies with similar designs. Two of the more common measures are Pearson's r and Cohen's d. Cohen's d describes the difference between the means of two groups normalized to the pooled standard deviation of the two groups. Pearson's r measures the association between two continuous variables. A problem arises when comparing a study that reports an r value with one that reports a d value. To address this problem, statisticians have developed methods to convert r values into d values, and vice-versa. The equations are listed below:

Many studies in the literature do not report effect sizes, and only report statistical significance results such as p values. Rosenthal and Rubin (2003) have developed a measure to account for this issue, requivalent, which can determine effect size from experimental designs comparing the means of two groups on a normally distributed outcome variable (Rosenthal and Rubin, 2003). This measure allows meta-analysis researchers to derive apparent effect sizes from studies that only report p values and sample sizes. First, one determines a t value from a t-value table by using the associated sample size and one-tailed p value. Using this t value, one can calculate requivalent using the following equation:  where df = degrees of freedom on which the p-value is based.
where df = degrees of freedom on which the p-value is based.
Limitations of Effect Size
We have built a justification for the reporting of effect sizes as a complement to standard statistical significance testing. However, we do not wish to mislead the reader to construe effect size as a panacea in quantitative analyses. Effect size indices should be used and interpreted just as judiciously as p values. Effect sizes are abstract statistics that experience biases from sampling effort and quality and do not differentiate among relationships of similar magnitude that may actually have more or less practical significance (Coe, 2002; Nakagawa and Cuthill, 2007; Ferguson, 2009). Rather, determination of what constitutes an effect of practical significance depends on the context of the research and the judgment of the researcher, and the values listed in Table 2 represent somewhat arbitrary cutoffs that are subject to interpretation. Just as researchers may have logical reasons to choose an alpha level other than p = 0.05 with which to interpret statistical significance, the interpretation of practical relationships based on effect size may be more or less conservative, depending on the context. For example, an r of 0.1 for a treatment improving survival of a fatal disease may be of large practical significance. Furthermore, as we mentioned earlier, one should always accompany the proper effect size measure with an appropriate confidence interval whenever possible (Cohen, 1994; Nakagawa and Cuthill, 2007; Ellis, 2010; Tressoldi et al., 2013). For example, Lauer et al. (2013) reported Cohen's d along with 95% confidence intervals to describe the effects of an administration of a values-affirmation exercise on achievement gaps between men and women in introductory science courses.
CONCLUSION
By highlighting the problems with relying on statistical significance testing alone to interpret quantitative research results, we hope to have convinced the reader that significance testing is, as Fan (2001) puts it, only one-half of the coin. Our intent is to emphasize that no single statistic is sufficient for describing the strength of relationships among variables or evaluating the practical significance of quantitative findings. Therefore, measures of effect size, including confidence interval reporting, should be used thoughtfully and in concert with significance testing to interpret findings. Already common in such fields as medical and psychological research due to the real-world ramifications of the findings, the inclusion of effect size reporting in results sections is similarly important in educational literature. The measures of effect size described here do not by any means represent the numerous possible indices, but rather are intended to provide an overview of some of the most common and applicable analyses for educational research and a starting point for their inclusion in the reporting of results. In addition to the references cited throughout this article, we recommend several informative and accessible authorities on the subject of effect sizes, summarized in Table 3.
| Introduction to effect sizes written for the nonstatistician and relevant to the educational researcher | Coe R (2002). It's the effect size, stupid: what effect size is and why it is important. Paper presented at the Annual Conference of the British Educational Research Association, held 12–14 September 2002, at the University of Exeter, UK. www.leeds.ac.uk/educol/documents/00002182.htm. |
|---|---|
| Theoretical explanation of effect size measures written for those with stronger statistical foundation | Cohen J (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Hillsdale, NJ: Lawrence Erlbaum. |
| Accessible and relevant reference for the practical application of effect size in quantitative research; includes directions for calculating effect size in SPSS | Ellis PD (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results, Cambridge, UK: Cambridge University Press. |
| A guide to implementing effect size analyses written for the researcher | Nakagawa S, Cuthill IC (2007). Effect size, confidence interval and statistical significance: a practical guide for biologists. Biol Rev Camb Philos Soc 82, 591–605. |
| American Psychological Association recommendation to report effect size analyses alongside statistical significance testing | Wilkinson L, APA Task Force on Statistical Inference (1999). Statistical methods in psychology journals: guidelines and explanations. Am Psychol 54, 594–604. |
ACKNOWLEDGMENTS
We thank Alla Sikorskii for helpful comments and edits on an earlier draft of this essay.