Development of the BioCalculus Assessment (BCA)
Abstract
We describe the development and initial validity assessment of the 20-item BioCalculus Assessment (BCA), with the objective of comparing undergraduate life science students’ understanding of calculus concepts in different courses with alternative emphases (with and without focus on biological applications). The development process of the BCA included obtaining input from a large network of scientists and educators as well as students in calculus and biocalculus courses to accumulate evidential support of the instrument’s content validity and response processes of test takers. We used the Rasch model to examine the internal structure of scores from students who have experienced calculus instruction in the two methods. The analysis involved three populations (Calculus 1, Calculus 2, and Biocalculus) for which the Calc 1 and Calc 2 students were not exposed to calculus concepts in a life science setting, while the Biocalculus students were presented concepts explicitly with a life science emphasis. Overall, our findings indicate that the BCA has reasonable validity properties, providing a diagnostic tool to assess the relative learning success and calculus comprehension of undergraduate biology majors from alternative methods of instruction that do or do not emphasize life science examples.
INTRODUCTION
Hosts of reports over the past few decades have pointed out the need for quantitative skills and conceptual mathematical foundations for undergraduates studying life science (American Association for the Advancement of Medicine, 2009; American Association for the Advancement of Science [AAAS], 2011; National Research Council [NRC], 2003; Steen, 2005). With the continuing growth of computational and data science approaches across the life sciences, these reports broadly agree that 21st-century biologists will be well-served through enhanced comprehension of the core quantitative concepts used throughout biology. Calculus provides one of the most fundamental mathematical frameworks that underlie science and is universally included as a core course for science, technology, engineering, and mathematics (STEM) students around the world. Calculus is a major component of quantitative training for biology undergraduates (Bressoud et al., 2013, 2015).
There has been consistent encouragement from the quantitative education community to link quantitative learning to real-world contexts. It is in part due to this that there have been intentional moves over the past four decades, since the time of Batschelet (1971), to develop mathematical materials in a biological context. The underlying assumption is that students with an interest in biology will more readily appreciate the importance of mathematics and be successful in developing their understanding of quantitative concepts such as those in calculus if the mathematics is framed in a biological context. This is consistent with recommendations from the National Council of Teachers of Mathematics that opportunities for students to experience mathematics in a context is important and that students are more likely to remember mathematics presented with real-world applications (National Council of Teachers of Mathematics, 2000). This is also congruent with a large body of reports and literature in K–12 science and mathematics instruction calling for an integrated science and mathematics curriculum (Hurley, 2001; Stinson et al., 2009) and use of mathematics in the science classroom (NRC, 2012).
Many national reports also encourage interdisciplinary approaches in STEM education (NRC, 2003; AAAS, 2011; President’s Council of Advisors on Science and Technology [PCAST], 2012). Regarding mathematics education, the PCAST (2012) report calls for a national experiment that includes developing and teaching mathematical concepts from an interdisciplinary approach. The mathematics education community has responded to this report in several ways, noting that the community should revisit course content, delivery methods, and educational assessment tools in undergraduate mathematics education (Holm, 2016).
Prior related efforts on calculus assessments include the Calculus Concept Inventory (Epstein, 2007). This was specifically developed as a tool to compare outcomes from interactive engagement and traditional teaching methods. In this sense, it was not a standard concept inventory across all core calculus concepts but focused on comparing alternative methods of instruction rather than emphasizing a particular student’s conceptual understanding. The objective was to have a tool for population-scale comparisons of samples of responses from students who experiences two different modes of instruction. There has been very limited work on the validity analysis of Epstein’s Calculus Concept Inventory, but there are no other calculus concept inventories at this time (Gleason et al., 2015, 2018). Carlson and collaborators developed a Precalculus Concept Assessment and a Calculus Concept Readiness instrument, both focused on precalculus concepts (Carlson et al., 2010, 2015). Gleason et al. (2018) critiqued the Calculus Concept Inventory, concluding that their data, from 1800 students enrolled in Calculus 1 courses, were consistent with a unidimensional model but expressing concerns about its content validity and reliability. The focus in their analysis was not on the comparision of alternative modes of instruction, which was the reason for which the inventory was developed.
Few assessments or inventories have focused across fields (i.e., explicitly interdisciplinary), but instead are discipline-centric. Given the push toward interdisciplinary education, it is important to determine the most effective practices to use concepts from outside mathematics in meeting mathematical learning goals. Likewise, it is important to have valid tools for assessing changes in students’ understanding, assessing the potential advantages of pedagogical interventions, and explicitly evaluating the contention that placing quantitative concepts in the concrete context of a domain of application will enhance student comprehension of the quantitative concept. The Statistical Reasoning in Biology Concept Inventory (SRBCI; Deane et al., 2016) is one of the first assessment tools to cross disciplinary bounds. Developers framed SRBCI questions using biology examples to assess students’ conceptions of statistical reasoning. Another assessment tool to assist in analyzing student quantitative comprehension in a life science context is BioSQuaRE (Stanhope et al., 2017), which considers algebra, statistical, and visualization concepts.
For decades calculus has been a required quantitative course for biology undergraduates, and biology students make up nearly 30% of all students taking Calculus 1 across all types of U.S. undergraduate institutions (Bressoud et al., 2013, 2015). The standard mechanism for teaching calculus in the United States has been through formal course sequences designed for a broad collection of science and engineering students. Historically, some institutions have either included life science students in these courses or have developed specialized courses for these students separate from and with somewhat different topic coverage than the standard science and engineering courses. Such specialized courses have sometimes been broadly inclusive of social science students as well, but some have focused explicitly on life science students, because they often make up a significant fraction of all STEM students at an institution. Over recent decades several biocalculus texts were developed that focus on standard calculus topics (Neuhauser, 2011; Adler, 2012; Schreiber et al., 2014) or take a somewhat broader perspective of quantitative topics to include linear algebra, probability, and discrete-time modeling (Bodine et al., 2014; Stewart and Day, 2015).
Our purpose is to explore the development and initial validity assessment of the BioCalculus Assessment (BCA), which aims to evaluate, in a comparative approach, undergraduate student understanding of calculus concepts embedded in the context of life science examples. Our objective is to develop a tool that can be effective in comparing alternative formats for student comprehension of concepts from calculus, particularly the alternative courses available to life science students at many U.S. institutions. Thus, the BCA has been developed explicitly to provide a means to assess the impact on calculus concept comprehension of different modalities of calculus instruction arising from different emphases and inclusion of concrete biological contexts. Options for students in this study include a standard science and engineering calculus sequence as well as a sequence designed specifically for life science students that emphasizes biology applications to enhance comprehension of calculus concepts. Three calculus concepts formed the basis of the BCA: rates of change, modeling, and interpretation of data and graphs.
It is our expectation that instruments such as the BCA and SRBCI can be applied to develop guidance regarding the impact of inclusion of life science disciplinary examples in calculus and statistical reasoning courses. Given the importance of quantitative methods across the life sciences, biology faculty may use the results of more expansive applications of the BCA to encourage their faculty colleagues who teach calculus to do so in a manner that is most effective for their students. This should also contribute to broader educational research questions regarding the impact of learning methods on student conceptual comprehension (Koedinger et al., 2013).
METHODS
The validity of the test, that is, the degree to which evidence supports the interpretation of test scores (Nunnally, 1978; Crocker and Algina, 1986; Pedhazur and Schmelkin, 1991; American Educational Research Association, American Psychological Association, and National Council on Measurement in Education, 2014), is an important aspect to examine when developing a test. Test validity is assessed through an accumulation of evidence that reinforces a test is measuring what it is intended to measure. The Standards for Educational and Psychological Testing indicate evidence such as content validity, response processes, and the internal structure of the test can be collectively used to support test validity (American Educational Research Association et al., 2014) and were used to frame our validation process for the BCA.
The BCA was primarily developed as a tool that educators and researchers could use to measure learning gains of students who are taught calculus instruction across different instructional modalities. Pellegrino et al. (2001) assert that every educational assessment is based on the following triangular principles: cognition, observations, and interpretation. During the creation of the BCA, we used input from subject-matter experts to create test items intended to measure understanding of calculus content across three focal areas (e.g., rates of change, modeling, and interpretation of data and graphs). These subject-matter experts have vast experience instructing and educating students within calculus and were instrumental in creating items for the assessment that are believed to adequately represent how students attain knowledge and develop competence within the subject. Focus groups were then conducted with students to gauge their perspectives on the connection of the items to course topics. We created a multiple-choice assessment as a means of observing students’ knowledge, as multiple-choice tests are easy to administer and score. Finally, with respect to the third foundation of the triangle, scores from pre to post on the instrument can be used to assess learning gains across different intervention strategies, and these scores can then be used to further research for different ways calculus content can be taught to undergraduate life science students.
Development of the BCA
Similar to the development of other assessment tools (e.g., Anderson et al., 2002; Garvin-Doxas and Klymkowsky, 2008; Jorion et al., 2015; Deane et al., 2016), the development of the BCA was an iterative process of collecting feedback across different stakeholder groups. More specifically, to develop the BCA, we identified core competencies to include on the assessment; consulted subject-matter experts in mathematics and biology to determine the most relevant test items to include on the instrument; modified the instrument based on undergraduate students’ feedback; completed pilot administration of tests; and evaluated the internal structure of the BCA using Rasch analysis.
We used the BIO2010 (NRC, 2003) and Vision and Change reports (AAAS, 2011) to identify a consensus of core calculus-related quantitative competencies for life science majors. We identified three major calculus concepts to include in the assessment based on our review of these reports: rates of change, modeling, and interpretation of data and graphs. We then constructed a pool of 52 initial test items that included these quantitative competencies interconnected to life science examples. We constructed test items through adaptation of questions from the following resources: the Calculus Concept Inventory (Epstein, 2013), Applied Calculus (Hughes-Hallett et al., 2013), Mathematics for the Life Sciences (Bodine et al., 2014), and Cornell’s Good Questions website (Cornell University, n.d.). Plausible distractors for each question were chosen based on our research team’s teaching experience of the concepts and consultation of the mathematics education literature for common student misconceptions related to the topics, including modeling and rates of change (Thompson, 1994; Thompson and Silverman, 2008; Bezuidenhout, 1998, 2001; Zandieh, 2000; Carlson et al., 2002). We did not find much research regarding misconceptions involving interpretations of data and graphs.
Content Validity
Content validity is an aspect of validity evidence that refers to the relevance, representativeness, and technical quality of items included on a test (Messick, 1995; American Educational Research Association et al., 2014). Evidence of content validity can be collected through systematic reviews by subject matter experts who give feedback on the adequacy of test items and the representation and relevance of the items to the domain (Reeves and Marbach-Ad, 2016).
We recruited subject matter experts in the interdisciplinary fields of mathematics and biology to help determine items to include on the BCA. All investigators leading this research are affiliated with the National Institute for Mathematical and Biological Synthesis (NIMBioS), a National Science Foundation–supported synthesis center that supports and promotes research and education at the interface of mathematics and biology. Investigators used NIMBioS’s large network of scientists and educators to recruit experts to review potential items for the assessment via an announcement in the NIMBioS bimonthly newsletter and through personal email invitations. A total of 84 experts completed an online rating form for the initial 52 questions. Each expert reviewed approximately four randomly assigned questions from the pool, with each of the 52 questions being rated by four reviewers. Each reviewer could also comment or suggest revisions.
Following the method provided by Rubio et al. (2003), we provided the draft questions for the instrument to the expert review panel with a response form and instructions on rating the items. For each item reviewed, each reviewer was asked to rate items for 1) representativeness of the concept, defined as an item’s ability to represent the content domain as described in the provided concepts for each item on a scale of 1–4, with 4 being the most representative; 2) clarity of the item, defined as how clearly and understandably the item is worded, on a four-point scale; and 3) overall quality of the question, defined as being free from bias, well written, and having plausible and mutually exclusive distractors (incorrect answers) on a four-point scale. Additionally, reviewers were provided space for comments to explain their rating responses and/or offer suggestions for question improvement.
We computed a content validity index (CVI) for each item from the review panel responses by counting the number of experts who rated the item a three or four on each rating criteria and dividing that number by the total number of experts reviewing the item. This, along with overall mean ratings for all three criteria were used to determine the most defensible items to include in the first iteration of the assessment. Items with a mean CVI less than 0.80 and an overall mean rating less than 3.3 were removed (Davis, 1992). This resulted in 35 test questions to consider for inclusion on the instrument. These 35 questions were then reevaluated by our research team, using comments and suggestions made by the expert reviewers to ensure representativeness of the concept, clarity of the item, and overall quality. After reevaluation, 23 of the highest-rated items were included in a first draft of the instrument.
Response Processes
Validity evidence on response processes of test takers is concerned with the fit between the performance of takers and the construct (e.g., knowledge of calculus concepts). Evidence of response processes is commonly assessed through think-aloud procedures that probe students’ rationalization and thought processes for answering particular questions (American Educational Research Association et al., 2014; Reeves and Marbach-Ad, 2016). This process can help developers ensure that the target population understands the question, ensure that wording of test items is appropriate, and include distractors that reflect students’ common misconceptions.
We conducted two focus groups with students to ensure that the students interpreted test items as intended, ensure that the language and notation used on the test were familiar to students, and obtain feedback from students about question wording and distractor choices. Criteria for student participation in the focus groups included undergraduates who had declared a biological science major and who had either taken 1) the AP Calculus exam but who had not taken calculus at the university, 2) two semesters of calculus at the university level, or 3) two semesters of Mathematics for the Life Sciences (a calculus course for life science majors that teaches calculus concepts in biological context). These criteria ensured that the focus group students would have the relevant educational background in mathematics to understand the concepts represented in the assessment. Email invitations to participate were sent to 463 prospective students, and a total of 19 students participated in one of two focus groups in Spring 2016 (10 and 9 students, respectively). All students had declared a biological sciences major, except one student who was from an environmental and soil science major. Nine of the students met the criteria of having AP Calculus exam credit, eight had taken two semesters of calculus at university, and two had taken two semesters of Mathematics for the Life Sciences. Ten of the focus group participants were female.
Two of the coauthors (K.S. and P.B.) and a graduate student facilitated the focus groups using the retrospective cognitive think-aloud process (Nolin, 1996). Additionally, two coauthors (S.L. and L.J.G.) with mathematics teaching experience each attended one of the focus groups to assist in answering questions from students. We provided students in each group with a paper copy of the instrument on which they could make notes, and students answered questions on the test using a personal response system or “clicker.” Clickers are remote-controlled devices that allow students to send their answers to a receiver connected to an instructor’s or researcher’s laptop computer, which instantaneously analyzes and displays the results. We asked students to answer test questions one at a time when prompted by a member of the research team, and after all students had provided their confidential responses to each question, we discussed the answer and distractors with the group using the following probes: 1) What do you think the question is asking?, 2)What is confusing about the question?, and 3) What words or phrases don’t you understand? (Bowling et al., 2008). Students also had space on paper copies of the instrument to write comments if they did not feel comfortable sharing with the group. Focus group sessions were recorded and transcribed. We analyzed data from the recorded student think-aloud process, along with notes from the research team and student paper copies of the test, for themes surrounding potentially confusing test wording, and results were used to modify question texts, answers, and distractors.
Owing to test fatigue, students gave minimal feedback regarding questions that appeared at the end of the instrument. A new version of the instrument with the edited questions in reverse order was piloted with 14 students. Using the same student criteria and recruitment strategies from the focus group stage, we recruited 14 students (of whom four had also participated in the focus group portion of the project) to participate in one of two pilot study groups (groups of six and eight students). All students in these pilot groups had declared a biological science major. Nine of the students met the criteria of having AP Math exam credit, two had taken two semesters of university calculus, and three had taken two semesters of Mathematics for the Life Sciences. Eight of the participants were female.
We provided paper copies of the instrument to the students, who were given the opportunity to provide written or oral comments about each question if they felt a question was confusing in any way. Members of the research team were available to answer any questions the students had. After these pilot tests, minor revisions were made to questions for clarity based on the feedback from the pilot study students. We used the resulting 22-question preliminary instrument from this phase of development in the evaluation phase of the study.
BCA In-Class Administration
Faculty in Calculus 1 (C1), Calculus 2 (C2), and Mathematics for the Life Sciences (BioCalc) administered the BCA in class over three semesters to students enrolled in their classes. C1 covers topics in differential calculus with no integral calculus and with emphasis on rates of change, and C2 expands on this to cover topics in integral calculus and series. These courses meet for 4 hours each week. C1 and C2 use a classical science and engineering calculus approach, emphasizing symbolics, graphing, and hand calculation, having limited applications mostly to physics, and allowing the use of graphing calculators. BioCalc is the second course of a two-course sequence, the first of which provides an overview of discrete mathematical topics including linear algebra; descriptive statistics; and discrete probability with applications to population modeling, allometry, and population genetics. The second course in the sequence, BioCalc, covers both differential and integral calculus, using biological examples particularly drawn from population biology, including exponential and logistic growth, and some physiological examples, including photosynthesis and blood flow. A focus throughout this two-course sequence is interpretation of data, simple modeling, and the use of a computational software package, MATLAB, to expose students to applications and numerical illustration of the key concepts in a biological context. BioCalc meets for 3 hours a week, and the focus on modeling, data, and computational software are emphases that do not appear in C1 and C2.We chose these courses because students within each course should be exposed to most, if not all, topics included on the assessment, and the courses are representative of how calculus topics are often split across calculus sequences. Essentially every biology major at the University of Tennessee, Knoxville, takes either the C1 and C2 sequence or BioCalc and its predecessor course covering topics in discrete mathematics. The coverage of the BCA content within C1, C2, and BioCalc is indicated in Table 1 by major concepts and subcontent with corresponding BCA question numbers. Many questions incorporated more than one of the three major concepts.
| Topics included in BCA | C1 | C2 | BioCalc | BCA question |
|---|---|---|---|---|
| Rates of change | ||||
| Derivative rules | X | X | 16 | |
| Interpreting/constructing graphs using derivatives | X | X | 7, 8, 11 | |
| Optimization | X | X | 11 | |
| Definite integral | X | X | 12, 13, 17 | |
| Fundamental theorem of calculus | X | X | 17 | |
| Net change as an integral of a rate | X | X | 12, 13, 17 | |
| Methods of integration | X | X | 13 | |
| Application of integrals | X | X | 12, 13, 17 | |
| Rate of change | X | X | X | 5, 7, 8, 12, 18 |
| Functions and modeling | X | X | X | 11, 12, 13 |
| Modeling | ||||
| Continuity | X | X | 4 | |
| Intermediate value theorem | X | X | 4 | |
| Definite integral | X | X | 15 | |
| Methods of integration | X | X | 15 | |
| Application of integrals | X | X | 15 | |
| Rate of change | X | X | X | 14, 20 |
| Functions and modeling | X | X | X | 3, 6, 20 |
| Analyzing and interpreting graphs | ||||
| Interpreting/constructing graphs using derivatives | X | X | 2 | |
| Rate of change | X | X | X | 1, 2, 9 |
| Functions and modeling | X | X | X | 10, 19 |
After the first administration of the 22-item BCA in Fall 2016, we removed two items from the instrument. We removed one item due to the high difficulty and low discrimination properties. We removed the second item because it was deemed to have unrealistic biological features after further review by our research team. In addition, 14 of the remaining 20 items included distractors of “none of the above” or “not enough information given.” We replaced these distractor options with plausible distractors in alignment with test development best practices (Kline, 1986; Downing, 2006; Brame, 2013; DiBattista et al., 2014).
A final revision to the test involved moving less difficult items to the beginning of the test and harder items to the end of the test. A meta-analytic review conducted by Hauck et al. (2017) found student performance on multiple-choice exams in which items are sequenced (i.e., ordered based on item difficulty) has no to minimal effect on overall test performance. However, test anxiety has been found to be reduced in item sequences of easy-to-hard test items (Tippets and Benson, 1989; Chen, 2012). Because the completion of the BCA was voluntary and taking the test had no influence on students’ grades, we decided to reorder test items in an easy-to-hard sequence in hopes of minimizing test anxiety, potentially encouraging students to complete the exam with minimal negative affects on overall test performance. The final BCA included 20 items and was administered to students in the Spring 2017 and Fall 2017 semesters.
Instructors administered the BCA to students during the last 25 minutes of class time within 2 to 3 weeks before the end of the semester. Students were encouraged to answer all questions and to provide a best guess to questions for which they did not know the answer. During the first two administrations of the BCA, we emailed students after course grades were submitted and asked them to provide consent to use their test scores as part of the validation research study. For the final test administration, we sought consent at preadministration, because we found that students were less likely to respond to emails when the semester was not in session. We used posttest scores from students who gave consent for their scores to be used in the analysis of this phase of the study, resulting in 206 student scores in the analysis (51 students from C1, 98 students from C2, and 57 students from BioCalc).
Internal Structure of the BCA
The internal structure of a test provides information regarding the degree to which the relationships among test items and test components conform to the construct on which the proposed test score interpretations are based (Messick, 1995; American Educational Research Association et al., 2014). Tests are developed to measure the amount of knowledge or the level of ability a person has regarding specific content domains. However, knowledge and ability represent latent variables, as they can only be assessed and measured indirectly. For these latent variables, tests are used as a tool to quantify a person’s ability level by how successfully he or she answers test items. One technique for assessing the internal structure of test scores is the Rasch model, proposed by Georg Rasch (1960).
The Rasch model is a psychometric technique that transforms raw scores into linear scales for person measures (ability) and item difficulty by modeling the probability of success (i.e., correct response) based on the difference between a student’s ability and an item’s difficulty. Boone (2016) advocates using Rasch techniques to improve the quality of tests in the life sciences, and Rasch models have been used to explore aspects of validity of concept inventories and other test instruments (Planinic et al., 2010; Arthurs et al., 2015; Deane et al., 2016; O’Shea et al., 2016). Rasch models are compatible with fundamental principles of measurement and therefore are useful tools for assessing whether data from physical science assessments conform to the model (Andrich, 2004).
In the Rasch model, items are assumed to be equivalent and item discrimination is set at 1, so that person ability and item difficulty can be compared using a common continuum (DeMars, 2010; Bond and Fox, 2015). Rasch models provide estimates for a person’s ability and item difficulty using logits. Logits are the natural log of an odds ratio, where an odds ratio is the ratio of the relative frequency of an event occurring over the relative frequency of it not occurring, when both frequencies are positive (Ludlow and Haley, 1995). Logits are equal interval units that allow scores to be additive and thus provide meaning to person and item comparisons (Bond and Fox, 2015). A 0 logit represents the mean or average item difficulty (or person ability). When the numerator represents the relative frequency of incorrect answers, positive logits represent more difficult test items, while negative logits represent easier, less difficult test items. This allows item difficulty to be on the same continuum as person ability, which is also represented such that negative logits indicate lower ability levels and positive logits represent higher ability levels (Tavakol and Dennick, 2013). A review of the spread in logits scores for person ability and item difficulty provides information regarding the representational spread of these indices along a continuum (Ludlow and Haley, 1995; DeMars, 2010; Bond and Fox, 2015).
Inherent assumptions to the Rasch model are unidimensionality and local independence. Unidimensionality refers to the assumption that all items are indicators of a single attribute of interest; therefore, scores are a representative summary of this attribute (Bond and Fox, 2015). Local independence of test items assumes that the probability of correctly answering any test item is independent of how examinees respond to other items on the instrument. While the literature indicates several techniques for assessing unidimensional linearity in the data, more research is necessary for exploring which methods are most appropriate when data are dichotomous (Tennant and Pallant, 2006). We explored the unidimensionality of the BCA data using principal components analysis (PCA) on residuals (Tennant and Pallant, 2006) and analyzed fit indices to assess violations of the assumptions (Bond and Fox, 2015; O’Shea et al., 2016). PCA analyzes the interrelationships among a set of variables (e.g., test questions) in order to condense information into a smaller set of variables, thus providing an objective case for creating summated scales (Hair et al., 2006). With PCA, eigenvalues (sum of squared loading for a factor) are used to represent the amount of variance accounted for by a factor. Multiple criteria can be used to explore the underlying structure of variable contribution, including the latent root criterion, which indicates that any factors present should account for the variance of at least a single variable (Hair et al., 2006).
In addition to PCA of unidimensionality, indices for item fit can provide further details on model fit. Indices for item fit include outfit and infit mean square (MSQ) statistics, which are chi-square statistics used to measure the association between the Rasch model fit and the data. Model fit is assumed when the chi-square ratio is ∼1. Outfit MSQs are sensitive to outliers, whereas infit MSQs are weighted and not influenced by outliers in the data (Smith, 1991; Linacre, 2002; Bond and Fox, 2015). Linacre (2002) suggests that misfit occurs when chi-square values are below 0.5 or above 1.5. The infit and outfit MSQ indices can be transformed to a standard normal scale using the Wilson-Hiferty transformation. These normalized statistics are referred to as Zstd outfit and Zstd infit and have an expected mean of 0 with an SD of 1 (Linacre, 2002; DeMars, 2010; Bond and Fox, 2015). Values of Zstd exceeding −2.0 and +2.0 suggest misfit of the data.
Local independence can be checked using Yen’s Q3 statistic, which calculates item-by-item correlations for item-pair residuals, where residuals are the differences between observed responses and the expected item responses predicted by the Rasch model (Yen, 1984; Embretson and Reise, 2000; DeMars, 2010; Wallace and Bailey, 2010). Local independence is assumed when there is no correlation or relationship between item-pair residuals (i.e., when correlation coefficients are 0), and local dependence is assumed with higher correlation coefficients. While there is not a uniformly accepted cutoff value for what correlation value is small enough to be indicative of local independence, a recent simulation study by Christensen et al. (2017) suggests critical values around 0.2 above the average correlation are reasonably stable.
The focus of our analysis was to determine whether the BCA operates similarly for students enrolled in different calculus-related courses. We conducted separate Rasch models for students enrolled in C1, C2, and BioCalc. We also used Wright maps, representing the relationship between the distribution of person and item measures using a vertical logit scale, to provide a visual summary for how data perform within the Rasch model (Bond and Fox, 2015). The analyses were completed using WINSTEPS v. 3.92.1 (Linacre, 2017) and R (R Core Team, 2017) with the libraries sirt (Robitzsch, 2018), ltm (Rizopoulos, 2006), and TAM (Robitzsch et al., 2018).
Human Subjects Approval
This study was completed in accordance with approval from the University of Tennessee’s Institutional Review Board (UTK IRB-15-02385-XP).
RESULTS
We assessed how content validity, response processes, and the internal structure of the test provide accumulated support for the overall validity of the BCA. Content validity was confirmed through feedback we received from a large network of scientists and educators in the interdisciplinary fields of mathematics and biology. These subject matter experts rated test items for concept representativeness, clarity of the item, and overall quality of the question. Only test items given high CVIs were included on the instrument. Further evidence based on response processes was obtained through focus groups and a pilot administration of the test with target student populations. We used feedback from these undergraduate students to modify and edit the BCA for wider administration. Finally, we used Rasch analysis to assess the internal structure of test items included on the BCA.
The BCA was revised between the initial administration and subsequent administrations. To determine whether rearranging the order in which an item appeared on the test created any bias in the likelihood of students getting the items correct or incorrect (e.g., would student fatigue or similar affect impact the analyses if data were combined across administrations), we conducted differential item functioning (DIF) analyses. DIF analysis is a technique used to compare the invariance of item difficulties across subsamples to assess item bias. Item bias occurs when a test item does not have the same relationship to the latent trait (i.e., calculus knowledge) across two or more examinee groups (Embretson and Reise, 2000; Bond and Fox, 2015). For our data, we created interaction terms between the items and the administration term and examined z-scores for interaction terms using a benchmark of −2 and +2. For any item exceeding an absolute z-score of 2, we examined effect sizes for the item to determine the strength of statistical significance. Only one of the 20 items was flagged as being significantly different across test administrations. For this item, “none of the above” on the Fall 2016 version was an attractive distractor but was replaced with another plausible distractor in the subsequent revision that was not chosen as frequently as the “none of the above” option. As 19 of the 20 items did not demonstrate item bias and we could explain the difference in response functioning for the flagged item, we determined that it was reasonable to use all three semesters’ test data. We then conducted separate Rasch models for C1, C2, and BioCalc.
Assumptions: Unidimensionality and Local Independence
We checked the assumption of unidimensionality for the Rasch models produced for each calculus course. PCA across courses had multiple eigenvalues above 1, suggesting multidimensionality in the BCA test items. Further review for how items loaded on factors was indeterminate; thus, we also used fit indices to analyze the presence of multidimensionality in the data. MSQ and Zstd infit and outfit statistics provided by WINSTEPS v. 3.92.1 for C1, C2, and BioCalc are presented in Table 2. Linacre (2012) suggests that outfit indices should be examined before infit indices; MSQ indices should be considered before Zstd; and high MSQs (indicative of underfit) should be considered before low MSQs (indicative of overfit). For our study, MSQ outfit and infit values generally fell within 0.5 and 1.5, indicating acceptable fit of the model (Linacre, 2002). However, for C1, the MSQ outfit values for items 14 (MSQ = 1.91, Zstd = 3.10) and 18 (MSQ = 1.78, Zstd = 1.70) exceed the MSQ cutoff of 1.5, and item 14 also exceeded the Zstd cutoff of +2.0. Items 18 (MSQ = 1.42) and 20 (MSQ = 0.33) for BioCalc also suggest potential misfit to the data. However, the Zstd for these items are within the −2.0 to +2.0 range. Note that item 14 deals with the underlying assumptions of an exponential population growth model, which is heavily emphasized in BioCalc but not in C1. All infit values, which are weighted and not influenced by outliers, fall within expected fit ranges.
| C1 | C2 | BioCalc | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Outfit | Infit | Outfit | Infit | Outfit | Infit | |||||||
| Item | MSQ | Zstd | MSQ | Zstd | MSQ | Zstd | MSQ | Zstd | MSQ | Zstd | MSQ | Zstd |
| 1 | 0.84 | −0.60 | 0.89 | −0.60 | 1.27 | 1.10 | 1.13 | 0.80 | 1.27 | 1.00 | 1.06 | 0.40 |
| 2 | 0.80 | −0.70 | 0.95 | −0.20 | 1.22 | 1.10 | 1.09 | 0.70 | 1.01 | 0.10 | 1.03 | 0.20 |
| 3 | 1.00 | 0.10 | 0.95 | −0.30 | 0.98 | −0.10 | 0.96 | −0.30 | 0.95 | −0.10 | 0.92 | −0.40 |
| 4 | 0.78 | −0.90 | 0.86 | −0.70 | 0.83 | −1.10 | 0.91 | −0.80 | 0.93 | −0.60 | 0.96 | −0.40 |
| 5 | 0.95 | −0.20 | 1.01 | 0.10 | 1.06 | 0.50 | 1.06 | 0.60 | 0.96 | −0.20 | 1.00 | 0.00 |
| 6 | 1.00 | 0.00 | 1.02 | 0.20 | 1.03 | 0.30 | 1.04 | 0.60 | 0.96 | −0.40 | 0.96 | −0.50 |
| 7 | 0.86 | −0.90 | 0.92 | −0.70 | 0.98 | −0.20 | 0.98 | −0.20 | 0.99 | 0.10 | 1.05 | 0.30 |
| 8 | 1.07 | 0.50 | 1.09 | 0.80 | 1.00 | 0.00 | 1.03 | 0.40 | 1.00 | 0.10 | 1.02 | 0.20 |
| 9 | 0.77 | −1.40 | 0.84 | −1.80 | 0.88 | −1.20 | 0.92 | −1.10 | 0.91 | −0.60 | 0.93 | −0.60 |
| 10 | 1.21 | 0.90 | 1.05 | 0.40 | 0.93 | −0.70 | 0.96 | −0.50 | 0.95 | −0.40 | 0.97 | −0.30 |
| 11 | 1.05 | 0.30 | 1.05 | 0.40 | 1.03 | 0.40 | 1.02 | 0.40 | 0.82 | −1.50 | 0.85 | −1.40 |
| 12 | 0.82 | −0.60 | 0.94 | −0.40 | 1.00 | 0.10 | 0.97 | −0.10 | 0.92 | −0.30 | 1.00 | 0.00 |
| 13 | 0.84 | −0.70 | 0.92 | −0.70 | 0.84 | −1.40 | 0.87 | −1.50 | 0.94 | −0.30 | 0.95 | −0.40 |
| 14 | 1.91 | 3.10 | 0.95 | −0.30 | 0.89 | −0.80 | 0.90 | −1.10 | 1.03 | 0.30 | 1.06 | 0.60 |
| 15 | 1.10 | 0.40 | 1.14 | 0.80 | 0.91 | −0.30 | 0.96 | −0.20 | 1.11 | 0.50 | 1.10 | 0.60 |
| 16 | 1.08 | 0.60 | 1.10 | 1.20 | 1.11 | 1.20 | 1.03 | 0.50 | 1.00 | 0.00 | 0.99 | −0.10 |
| 17 | 1.04 | 0.20 | 1.02 | 0.20 | 1.14 | 1.00 | 1.08 | 0.80 | 1.17 | 0.80 | 1.06 | 0.40 |
| 18 | 1.78 | 1.70 | 1.27 | 1.10 | 1.32 | 1.20 | 1.15 | 0.90 | 1.42 | 1.70 | 1.18 | 1.00 |
| 19 | 0.98 | 0.10 | 0.97 | 0.00 | 1.02 | 0.20 | 1.07 | 0.30 | 0.92 | −0.10 | 1.04 | 0.20 |
| 20 | 0.98 | 0.10 | 1.00 | 0.10 | 0.69 | −1.20 | 0.86 | −0.70 | 0.33 | −0.90 | 0.85 | 0.00 |
We checked for local independence of the BCA items by calculating Yen’s (1984) Q3 statistic for the C1, C2, and BioCalc populations. Correlation matrixes of item-pair residuals are provided in the Supplemental Material. The average residual correlations for C1, C2, and BioCalc each rounded to −0.05. Residual correlations above 0.15 were then flagged as potential violations of local independence. Of the 190 item-pairs, 18 (9%) coefficients for C1, 11 (6%) coefficients for C2, and 19 (10%) coefficients for BioCalc exceeded the adjusted critical value of 0.15. For C1, item-pair 2 and 4 resulted in the maximum Q3 value of 0.31. For C2, item-pair 13 and 20 resulted in the maximum Q3 value of 0.31; and for BioCalc, item-pair 4 and 5 resulted in the maximum Q3 value of 0.37. We determined that, overall, local independence was still reasonably valid, as 1) coefficients produced across correlation matrices were still relatively small, 2) item-pairs flagged for local dependence were not consistent across population groups, and 3) no relationship was evident between test items when reviewing item-pairs with coefficients above the threshold. Hence, this suggests that the student responses to each test item are independent of their responses to other test items.
Item Characteristics and Wright Maps
Item difficulties (in logits) ranged from −1.81 to +1.83 for C1, from −1.90 to 2.27 for C2, and from −1.94 to 2.79 for BioCalc; see Table 3. Note that the ranges of item difficulties for the three major calculus concepts were similar when compared for the three courses. For example, for the assessment questions emphasizing interpreting data and graphs, the ranges of item difficulty scores were −1.81 to 1.83 for C1, −1.78 to 2.27 for C2, and −1.94 to 1.19 for BioCalc. We used Wright Maps (shown in Figure 1, a–c, by calculus population: C1, C2, and BioCalc) to demonstrate the person ability levels and item difficulty levels of the 20 BCA items. Each map shows the difficulty level of the BCA items on the right-hand side, and person ability estimates on the left using the same units/metrics. Persons represented on the left next to a given item difficulty level represent those test-takers with a 50% chance of getting the item correct. In general, the pattern of item difficulties across the different populations of calculus students is similar, with item difficulty being more evenly dispersed for C1 and C2 students. However, two inconsistencies suggest differences across students in the course populations. Item 12 is indicated as a relatively easy item for C2 and BioCalc students to get correct, but is one of the harder items in the pattern for C1 students. This discrepancy is likely attributable to the differences in content covered within the courses, such that students in their first semester of calculus have not been exposed to the material associated with this item (integrals), whereas the other students have. Another unusual item pattern is with item 7, which is placed as a slightly easier than the mean item for students in C1 and C2, but is a more difficult item for students in BioCalc.
| Subject | Question | C1 | C2 | BioCalc |
|---|---|---|---|---|
| Graphs | 1 | −1.56 | −1.78 | −1.8 |
| Graphs | 2 | −1.81 | −1.49 | −1.94 |
| Graphs | 9 | 0.07 | −0.5 | 0.29 |
| Graphs | 10 | 0.65 | 0.5 | 0.04 |
| Graphs | 19 | 1.83 | 2.27 | 1.19 |
| Model | 3 | −1.22 | −1.36 | −1.79 |
| Model | 4 | −1.56 | −1.1 | −0.22 |
| Model | 6 | −0.63 | −0.03 | −0.29 |
| Model | 14 | 0.59 | 0.74 | 0.17 |
| Model | 15 | 0.98 | 1.62 | 0.9 |
| Model | 20 | 1.46 | 1.87 | 2.79 |
| ROC | 5 | −1.02 | −0.9 | 0.2 |
| ROC | 7 | −0.83 | −0.55 | 1.1 |
| ROC | 8 | −0.83 | −0.59 | −0.94 |
| ROC | 11 | 0.55 | 0.11 | 0.17 |
| ROC | 12 | 0.7 | −1.9 | −1.58 |
| ROC | 13 | 0.39 | 0.67 | 0.25 |
| ROC | 16 | −0.21 | −0.17 | −0.14 |
| ROC | 17 | 0.92 | 0.85 | 0.78 |
| ROC | 18 | 1.53 | 1.75 | 0.83 |
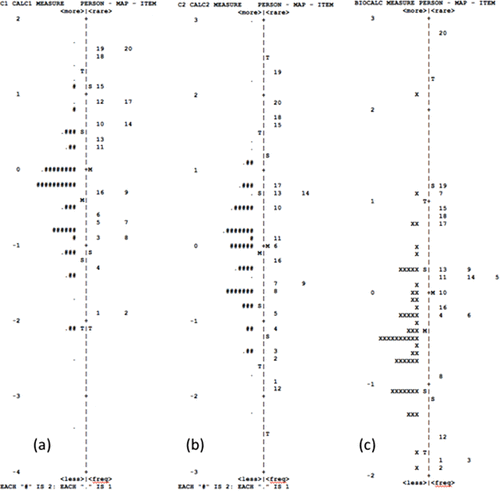
FIGURE 1. Wright maps for C1 (a), C2 (b), and BioCalc (c) for all BCA items. Wright maps demonstrate item difficulties and person abilities using same-scale units, showing a robust spread of levels. Note that the three maps have different scales and cannot be compared directly.
Raw Scores versus Logit Ability Estimates
Raw scores for students’ abilities do not account for differences in item difficulties across test questions; thus, a difference of missing 10 points on a test may not represent students missing items of the same caliber or item difficulty. Rasch models provide a solution to a fundamental issue within social science data in which equidistance is not maintained across scores. The conversion of raw scores into logits for estimating item difficulty and person ability provides linear, equal distance between scores, thus allowing for more accurate and precise comparison of ability levels. We examined the Pearson product-moment correlations between students’ raw scores and their Rasch ability estimates to see whether the raw scores could be used as appropriate estimates for students’ abilities. Product-moment correlations between students’ raw scores and their Rasch-predicted ability estimates were 0.98 for C1, 0.88 for C2, and 0.77 for BioCalc. While the correlation coefficient for C1 represents a strong, positive linear relationship between Rasch scores and raw scores, the lower coefficients for C2 and BioCalc reinforce using Rasch model estimates as the most appropriate estimates for assessing gains in student learning.
DISCUSSION
Calculus has historically been a major component of quantitative training for biology undergraduates. Because the majority of undergraduate life science curricula require calculus in some form, there continues to be a need for the BCA to assess student comprehension of calculus with different teaching methods and different levels of biological applications. The BCA measures a subcomponent of the broader range of quantitative skills to which life science students are exposed. Tools to assess conceptual understanding of calculus in a cross-disciplinary way are needed to assess changes in student understanding, examine potential advantages of pedagogical interventions, and explicitly evaluate whether placing quantitative concepts in this discipline-specific domain enhances student comprehension of calculus concepts. The availability of the BCA provides opportunities for faculty and other researchers to participate in the ongoing national experiment in life science quantitative education through which institutions offer different routes for calculus training for life science students, which may be broadly useful, particularly as new fields such as data science emerge and are connected to life science programs.
The BCA is designed to be administered in class to undergraduate students. Multiple-choice tests are simple to administer and quick and easy to analyze, and thus permit instructors to rapidly assess the conceptual abilities of students (Adams and Wieman, 2011). The BCA may be used on a broader scale to enable instructors to better target their teaching toward their students’ understanding, assess gains in conceptual knowledge, and evaluate teaching interventions. The high correlations between Rasch model produced scores and raw test scores supports using raw scores as an adequate means for assessing student ability of calculus knowledge, so that evaluation of student test scores may be accessible to instructors who may not be familiar with Rasch models.
We created the BCA to fill a measurement gap for assessing learning gains of students with life science backgrounds who may learn calculus within an interdisciplinary quantitative biology course or within a traditional university calculus course (often geared toward mathematics and engineering majors). Our assessment of the validity of the BCA indicates the instrument is a valid diagnostic tool to assess calculus comprehension in undergraduate biology majors who learn calculus within a quantitative course designed specifically for life science students, but also is appropriate to compare scores for students from traditionally taught calculus courses. Together, results from our assessment of the content validity, response processes, and internal structure of the instrument provide accumulated support for the validity of the BCA (American Educational Research Association et al., 2014).
While the instrument demonstrates evidence for the validity of the test, we recognize several limitations of our findings that future users of the test should consider. Overall fit indices indicated that most of the 20 BCA test items were unidimensional (i.e., measure a single construct of calculus knowledge) and locally independent for C1, C2 and BioCalc. However, slight misfit in unidimensionality was observed when question 14 was included on the test for C1. Additionally, some item-by-item comparisons for local independence were outside typical cutoff values, but further review determined that overall evidence supported local independence of the test (similar to findings from Deane et al., 2016, and Wallace and Bailey, 2010). Within the sequence of C1, the pattern of difficulty for item 12 did not fit the pattern of easiness represented for students in C2 and BioCalc. This is not surprising, because the topic of focus in item 12, integration, is not included in C1 but is included in C2 and BioCalc. Note that the BCA includes four questions (12, 13, 15, and 17) that assess comprehension of integrals, and all of these, except for item 12, had positive difficulty scores for all three course populations. As this material is not covered in the C1 sequence, the differences in the pattern make intuitive sense and also suggest that future users of the test would need to determine which items reflect the material covered within the courses being assessed.
Comparing the difficulty scores for the items indicates that students across the set of courses for this study can understand rates of change from simple data in a chart or a graph (e.g., items 1 and 2) and the implications of exponential rates of growth from simple population data to estimate population sizes at various times (e.g., item 3). At the other end of the difficulty scale, the representation of functions using log-log graphs is not readily understood (e.g., item 19). This topic of nonlinear scaling, though arising in many areas of biology, is not generally emphasized in standard calculus courses (e.g., C1 and C2). Even though log-log plots are emphasized in BioCalc, the results indicate that these students generally also did not obtain conceptual understanding of nonlinear scaling. Similarly, integration of trigonometric functions scored at high difficulty for all courses (e.g., item 15). The implication of these results is that an emphasis on nonlinear functions in calculus courses for life science students should be encouraged. Conceptually, item 14 required responses about the assumptions in a simple population growth model and was of medium difficulty across all courses, while other items dealt with particular numeric or symbolic answers. So emphasis on determining basic underlying model assumptions might be appropriately increased to enhance student conceptual foundations.
The spread of difficulty across the 20 BCA items suggests some robustness of the test to assess differing levels of student abilities. As Figure 2 illustrates, across the set of three main concepts included in the BCA, there was a similar range of difficulty in terms of students’ responses. Thus, across these concepts, for the sample of students in our study, no single concept stood out as requiring major reinforcement over others. The ranges of item difficulty scores for the three courses were similar when considered as disaggregated into the three major calculus concepts, providing further evidence that the BCA is an appropriate tool to compare different methods of instruction. Further research is needed to determine whether this result holds when the BCA is more broadly applied to larger populations of students, as validation is an ongoing accumulation of evidence from various populations across different contexts (Pedhazur and Schmelkin, 1991; Messick, 1995; American Educational Research Association et al., 2014). As the instrument is more broadly disseminated, more data collection might help to further validate the instrument across different populations and contexts. For instance, a broader data set may add evidence to evaluate why question number 14 did not operate according to the predicted Rasch model for C1 students, and a larger sample size could also help to gain a better understanding of scores for local independence found in this study.
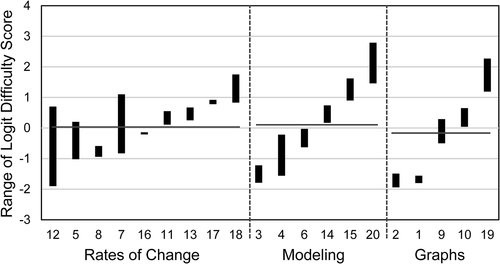
FIGURE 2. Ranges of all the logit difficulty scores from the three courses are shown in groups by the calculus concepts.
Feedback from future BCA users is welcome and will be used to refine and further evaluate the BCA. One limitation of the current study is that we did not account for various levels of exposure to calculus among students (i.e., an assumption was made that all have had similar precalculus courses before the assessment, and we did not account in any way for a diversity of prior calculus experience). Studying the effects of the variety of degrees of exposure to calculus on assessment results is an interesting area for further exploration.
ACKNOWLEDGMENTS
This material is based upon work supported by the National Science Foundation through NSF award DUE- 1544375, EAGER: Assessing Impacts on Student Learning in Mathematics from Inclusion of Biological, Real-World Examples, to the University of Tennessee. Additional support was provided by the NSF through award DBI-1300426, National Institute for Mathematical and Biological Synthesis, to the University of Tennessee. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF. We thank the panel of expert reviewers, students who participated in focus groups and pilot studies for assistance in question refinement, instructors who administered the test, and students who took the exam and provided consent to use their scores. We also thank Virginia Parkman and Gregory Wiggins for their efforts in data management and graphics during the research project. This article benefited greatly from the very helpful comments of several reviewers and the editor. For access to the BioCalculus Assessment, please contact Suzanne Lenhart at slenhart@utk.