Applying Graph Theory to Examine the Dynamics of Student Discussions in Small-Group Learning
Abstract
Group work in science, technology, engineering, and mathematics courses is an effective means of improving student outcomes, and many different factors can influence the dynamics of student discussions and, ultimately, the success of collaboration. The substance and dynamics of group discussions are commonly examined using qualitative methods such as discourse analysis. To complement existing work in the literature, we developed a quantitative methodology that uses graph theory to map the progression of talk-turns of discussions within a group. We observed groups of students working with peer facilitators to solve problems in biological sciences, with three iterations of data collection and two major refinements of graph theory calculations. Results include general behaviors based on the turns in which different individuals talk and graph theory parameters to quantify group characteristics. To demonstrate the potential utility of the methodology, we present case studies with distinct patterns: a centralized group in which the peer facilitator behaves like an authority figure, a decentralized group in which most students talk their fair share of turns, and a larger group with subgroups that have implications for equity, diversity, and inclusion. Together, these results demonstrate that our adaptation of graph theory is a viable quantitative methodology to examine group discussions.
INTRODUCTION
Collaboration and small-group discussions form the foundation for many evidence-based instructional practices and are effective means of enhancing student learning in science, technology, engineering, and mathematics (STEM). Learning theories such as constructivism provide broad explanations for the theoretical basis of group discussions (National Research Council, 2000; Chi, 2009; Chi and Wylie, 2014). Empirically, group discussions help students develop cognitive skills such as critical thinking (Webb, 1982b; Gokhale, 1995; Bligh, 2000), problem solving (Heller et al., 1992), and disciplinary understanding (Freeman et al., 2014); enhance important skills such as communication (Webb and Farivar, 1994) and metacognition (Webb and Mastergeorge, 2003; Veenman et al., 2006; Bromme et al., 2010); improve affect such as interest and motivation (Skinner and Belmont, 1993; Ryan, 2000); and increase completion rates in courses and persistence in STEM majors (Tinto, 1997; Freeman et al., 2014; Loes et al., 2017; Figure 1, right).
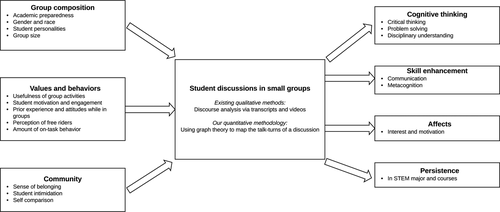
FIGURE 1. Small-group discussions in STEM learning. Student discussions can be influenced by a number of factors, including group composition, sense of belonging, and values and behaviors related to collaborative activities. The dynamics and quality of these discussions can affect student outcomes, such as cognitive learning, development of process skills, affect, and persistence. In the existing literature, quality of small-group discussions is typically analyzed by discourse analysis. In this study, we adapt graph theory methodologies to examine the dynamics of these discussions. Citations are available in the body of the text.
The effectiveness of discussions depends on how the members of a group interact with one another, and many factors can influence group dynamics (Figure 1, left). Some of these factors are related to group composition, including academic preparedness (Hillyard et al., 2010), gender and race (Springer et al., 1999), student personalities (French and Kottke, 2013), and group size (Bligh, 2000; Aggarwal and O’Brien, 2008; Fiechtner and Davis, 2016). Other factors involve what students value and how they behave. Group discussions are only effective when students find the activities useful (Blumenfeld et al., 1996) and thus are motivated to engage with the activities (Machemer and Crawford, 2007; Micari et al., 2010). Similarly, prior experience and attitudes while working in groups (Forrest and Miller, 2003; Hillyard et al., 2010), perception of free riders (Hall and Buzwell, 2012), and the amount of on-task behavior of other group members (Latané et al., 1979; Aggarwal and O’Brien, 2008) can influence group dynamics. Community also plays an important role. Positive or negative influences on group dynamics are affected by a strong sense of belonging (Anderman, 2003; Freeman et al., 2007), intimidation by fellow group members (Micari and Drane, 2011), and comparison of one’s academic and social standing relative to other group members (Micari and Pazos, 2014).
In the literature, the substance of group discussions is commonly studied using qualitative methods, specifically discourse analysis (Figure 1, middle). Discourse analysis is defined as “the study of language-in-use” (Gee, 2011, p. 8), which considers how and why certain actions occur and how they become reality (Dunn and Neumann, 2016). Typical applications of discourse analysis in this area include understanding student comprehension, knowledge construction, and cognition (King, 1994; Fall et al., 2000; Anderson et al., 2001; Sfard, 2001; Kittleson and Southerland, 2004; Webb et al., 2006; Molenaar and Chiu, 2017); scientific argumentation and the substance of student conversations (Chiu, 2008a,b; Soter et al., 2008); student participation and communication (Sfard and Kieran, 2001; Empson, 2003); collaboration (Webb et al., 2002; Wells and Arauz, 2006; Premo and Cavagnetto, 2018); classroom and student dynamics (Nystrand et al., 2003; White, 2003; Ikpeze, 2007); and students’ emerging STEM identities in the classroom (Brown et al., 2005; Bishop, 2012; Wood, 2013; Kumpulainen and Rajala, 2017). However, most of these methodologies capture group discussions only for short durations for in-depth qualitative analyses and have certain limits in tracking how the conversations progress over time in a quantifiable manner.
The dynamics of how students interact and talk with one another in groups is at the crux of many different active-learning strategies and is also critical for equity for and inclusion of all students. To understand how different factors contribute to group dynamics and how different interactions lead to different student outcomes, it is imperative to be able to quantify how students participate and engage in groups (Figure 1). By quantifying how students interact and talk with one another in groups, we can identify factors that contribute to how marginalized and minoritized students may or may not be able to engage in groups. Furthermore, understanding the dynamics of student group discussions will help elucidate the mechanisms by which different types of interactions contribute to different student outcomes.
Currently, there are not sufficient quantitative tools to examine the dynamics of student group discussions. In this paper, we adapt graph theory to track how students communicate with one another in groups by recording the order in which each participant talks and analyzing these talk-turn patterns in a quantitative manner. Our methodology is developed and tested through three iterations of data collection and two major refinements of the mathematical calculations. Case studies are selected to demonstrate the potential patterns observed and highlight the utility of this methodology in biology education research.
THEORETICAL FRAMEWORK
There are several learning theories that deal with the fundamental basis of how people learn. We focused on social constructivism because of its relevance to group learning, and we also used cultural-historical activity theory (CHAT) to understand how students interact to make a collaborative group effective. Social constructivism posits that learning is a social process, emphasizing how student interactions in a group or classroom setting contribute to how they learn, think, and converse within the academic community (Hirtle, 1996; Adams, 2006; Powell and Kalina, 2009). Vygotsky postulated that people learn by social interaction, and Dewey believed that learners are part of a greater community that teaches and enriches all of its members (Hirtle, 1996). From Vygotsky and Dewey, it can be said that an open environment where students are able to collaborate with one another is essential for knowledge building (Powell and Kalina, 2009). This social process of learning forms the foundation of active-learning strategies, which have been shown to be effective across STEM disciplines and settings (Freeman et al., 2014). Social constructivists strive to provide an open environment for students to share their thoughts freely and to give students democratic control over their learning to foster a sense of deeper inquiry and learning (Davydov, 1995; Hirtle, 1996; Adams, 2006). In this environment, instructors serve as facilitators in the discussions and provide scaffolds for students whenever necessary (Davydov, 1995; Adams, 2006; Powell and Kalina, 2009). To truly understand learning in the social constructivist view, we need to examine how students interact with one another and with their instructors.
Active engagement with spoken or written language is an important medium for learning, according to the social constructivist perspective (Hirtle, 1996). When students feel welcomed and their communication styles acknowledged, they are more willing to engage and get more out of activities in the classroom (Hirtle, 1996; Powell and Kalina, 2009). In addition, a welcoming and inclusive environment allows students to freely contribute different perspectives and experiences, which can help enhance student understanding of the subject matter (Davydov, 1995; Adams, 2006; Powell and Kalina, 2009). However, differences in communication styles can also bring another set of challenges, which may arise based on how students view other ethnicities and how willing they are to work with others (Atwater, 1996; Powell and Kalina, 2009). To foster an inclusive classroom, it is imperative to be able to quantify how different students may or may not engage with the group learning environments, so we can understand the potential biases that are present, among other factors that contribute to an effective collaboration in the learning process.
CHAT is another theoretical framework relevant to student learning and especially articulates the connection between what people think and what people do (Roth, 2004; Roth et al., 2009; Nussbaumer, 2012). Specifically, second-generation CHAT considers how the relationships among people (the subjects), the activity (the object), tools, rules, community, and division of labor can all affect the final outcome (Figure 2), and a core idea of CHAT is the interconnectedness of these various components (Roth, 2004; Roth et al., 2009; Nussbaumer, 2012). In the literature, CHAT has been used to observe student–student relationships and student–instructor relationships by examining the division of labor, the learning community, and the unwritten rules guiding these relationships (Nussbaumer, 2012). Researchers have also used CHAT to examine how variations in the subject and composition of the community contribute to the learning process by observing how the combined effects of students’ demographics, cultural backgrounds, and perceptions of learning connect to the outcome (Roth et al., 2009). Connections defined across the different components in CHAT cannot necessarily be easily seen directly (Roth et al., 2009; Roth, 2012), thus necessitating a methodology that can quantify some of these connections.
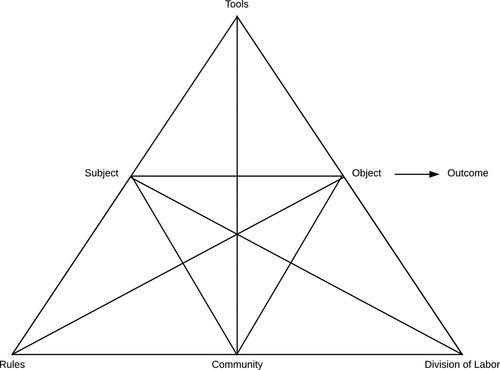
FIGURE 2. Cultural-historical activity theory (CHAT). In this study, we used CHAT to consider how the relationships among students (the subjects), the learning activity (the object), tools, rules, community, and division of labor in small groups can contribute to the final learning outcome. CHAT emphasizes the interconnectedness of these various components. These connections are not always easily observable, thus necessitating a methodology that can quantify some of these connections. Specifically, we developed a methodology based on graph theory to quantify the division of labor, the interactions among students and peer facilitators in small groups (the community), and potentially hidden rules that guide how different students may or may not engage with the activity (the object).
METHODOLOGICAL FRAMEWORK
Graph Theory
We chose graph theory to model the order in which students talk in a group, which we consider a proxy for the dynamics of the discussion. Graph theory uses a set of mathematical principles and formulas to examine the relationships among objects of interest (Zweig, 2016). In its simplest form, a graph consists of nodes and edges (Godsil and Royle, 2001): Nodes represent the objects of interest, and edges represent the connections between them (Figure 3A). In our methodology, we model the participants of the group as nodes. When one participant talks after another, an edge is connected between them, and we define such as an edge as a talk-turn. There are several interpretations for edges. They may track how the discussion turns from one participant to another, who is willing to speak after others, and/or who contributes ideas that could be expanded upon or responded to. An edge does not necessarily suggest that two participants talk directly to each other; in fact, when a participant talks, everyone else in the group may be listening, but only one person talks in the next turn. Thus, an edge only indicates that one participant talks after the other.
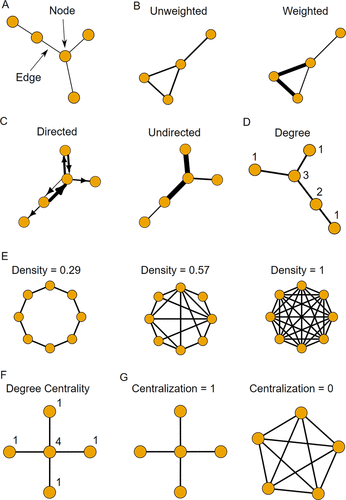
FIGURE 3. Relevant graph theory parameters. (A) In a graph, nodes represent the objects of interest, and edges represent the connections between them. The graph shown here contains five nodes and four edges. (B) Edges can be weighted, typically to represent frequency of some sort, or unweighted. (C) Graphs can be directed (with edges pointing from one node to another) or undirected (with edges simply connecting two nodes). Directed graphs have more information, as they show how much reciprocation is present between a pair of nodes. (D) Degree indicates the number of edges connected to a node. The degree of each node is labeled. (E) Three graphs with their associated densities: As more edges are added, density increases. (F) Degree centralities of a graph with five nodes: The degree centrality is exactly the degree of each node. (G) The centralization of two graphs that both have five nodes: The left graph has a higher centralization, because it is more centralized on node 1, while the right graph is less centralized.
Edges have additional important features. First, edges can be weighted, usually to present frequency (Godsil and Royle, 2001; Figure 3B). We use edge weight to represent the number of times one participant talks after another participant, capturing the frequency of talk-turns between any two participants. Second, edges may be directed (pointing from one node to another) or undirected (simply connecting two nodes; Godsil and Royle, 2001; Figure 3C). In our methodology, the edges in a directed graph track the sequential order in which participants talk. We used a directed graph rather than an undirected graph, because we can track the reciprocation between a pair of nodes; that is, if one person responds more after another person but not the other way around. On the other hand, an undirected graph shows only that there was a talk-turn between the two nodes. Tracking the directionality of conversations is important for understanding the equity and inclusion of different students in group learning environments; for example, Webb and Kenderski (1985) found that males are less likely to respond to females’ requests in conversations, while females are more likely to reciprocate.
Graphs can have many mathematical parameters, and we selected relevant parameters to capture information on the dynamics of group discussions (Table 1). Degree and density are related parameters dealing with the number of connections that nodes have with one another (Figure 3, D and E); here, these parameters represent how many participants talk after another participant. Degree is a parameter of individual nodes and measures the number of edges connected to a node (Zafarani et al., 2014). Density is a parameter for the entire graph and is the total number of edges in a graph normalized to the maximum number of possible edges (Borgatti et al., 2013). Density for a given graph ranges from 0 to 1 in value and is calculated as

| Parameter | Definition | Our methodology | Social network analysis |
|---|---|---|---|
| Node | An object of interest | Student or facilitator | Person |
| Edge | A connector between two nodes | Talk-turn between two individuals | Flow of information between two people |
| Direction | Defines which node points to another using the edge | Indicates which individual talks after the other | Indicates which person has ties to the other |
| Weight | A number associated with an edge | Frequency of talk-turns between two individuals | Frequency of information flow between two people |
| Degree | Number of edges connected to a node | Number of people an individual talks before/after | Number of people an individual has ties to |
| Density | Number of edges divided by number of possible edges | Talk-turns occurring among different individuals | Interactions occurring among different people |
| Centrality | A number for the importance of a given node in the graph | Amount of talk-turn contributions for an individual | Amount of influence of each person |
| Centralization | A number for the importance of the central node | Dependence of a group on its most active individual | Dependence of a network on its most active person |
| Subgraph | A smaller graph within a graph | Individuals who talk after each other more | Individuals who have closer ties to each other |
Nodes with higher degrees indicate participants who engage in talk-turns with or between more people. Graphs with higher density values indicate greater overall diversity in participants talking after one another; in other words, participants are talking after different people more often.
Centrality and centralization are another pair of related parameters for individual nodes and the entire graph respectively (Figure 3, F and G). Centrality captures the notion that some nodes are more important to the connections of edges in a graph than others (Zafarani et al., 2014). Centrality can be estimated using a variety of methods that emphasize different interpretations for what an edge means in a graph. Many types of centrality deal with connections of edges beyond two nodes and are often used to examine the flow of information across many people. In this study, we model talk-turns between two participants as the smallest unit of analysis; we also do not imply that information is flowing only from one participant to the next, as everyone in the group can be listening to the information. Thus, degree centrality is the most appropriate, because it relies only on the degree of a node or the number of edges connected to a node. Degree centrality for a given node is calculated as

A node with high degree centrality means that the participant talks before and after many different people, which is another proxy for active participation. This parameter provides additional information to the frequency of talk-turns (edge weights).
While centrality is a parameter for individual nodes, centralization is the equivalent parameter for the entire graph and measures whether the graph is centered around a particular node (Borgatti et al., 2013). Similarly, we use degree centralization, because it does not involve edges beyond two nodes. Degree centralization for a given graph ranges from 0 to 1 and is calculated as

We use degree centralization to determine to what extent a discussion is dominated by its most active participant.
Finally, subgraphs are smaller graphs within graphs (Godsil and Royle, 2001). We use subgraphs to determine highly connected subgroups within the larger group of participants based on edges and their relative weights (Supplemental Material). High connectedness means that individuals talk more frequently after one another within the subgroup than after participants outside the subgroup. Within the subgroup, participants may be willing to speak after one another or are more likely to contribute ideas among one another that could be expanded upon or responded to.
Comparison to Similar Frameworks
A similar research methodology, social network analysis, has emerged in recent years in biology and physics education research (Grunspan et al., 2014; Bruun, 2016). However, social network analysis and graph theory are not the same, even though their names are often used interchangeably in the literature (Zweig, 2016). Graph theory is a branch of mathematics that seeks to understand how different parameters and graphical structures are related to one another (Zweig, 2016), and social network analysis is a specific application of graph theory more focused on relating the properties of the graph to understand the flow of information and social capital, as well as the formation of beliefs and identities, within a group of people (Knaub et al., 2018). In this paper, we use graph theory to track the talk-turns among participants in small-group discussions rather than the flow of information in a social network (Table 1).
METHODS
Study Context
This study was conducted at a large, private, not-for-profit, doctoral university (highest research activity), with an undergraduate profile that is 4-year, full-time, primarily residential, more selective, and lower transfer-in, as reported by the Carnegie Classification of Institutions of Higher Education (McCormick and Zhao, 2005). We observed groups of introductory biology students tackling conceptual problems related to their course work in an optional, peer-led academic program (Drane et al., 2005, 2014; Light and Micari, 2013). In this program, consistent groups of five to seven students meet weekly to work with peer facilitators who have previously excelled in the course (Swarat et al., 2004), and groups were observed in the second half of the academic quarter. This study was approved by the Institutional Review Board at Northwestern University.
Data Collection
Our methodology was developed through three iterations of data collection based on observations of students solving problems in groups (Figure 4). In the first iteration, qualitative notes and memos were written during observations to track the discussions. Partial talk-turn data were included as part of the notes. In the second iteration, the relative physical positions of participants in each group were recorded in hand-drawn diagrams. Each talk-turn between any two participants was drawn as a line between them, and the number of talk-turns was tracked by tally marks. This resulted in undirected data for our graph theory calculations.
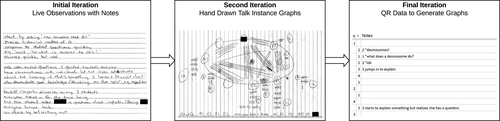
FIGURE 4. Three iterations of data collection. In the first iteration, qualitative memos were recorded in live observations of student groups (n = 8). In the second iteration, hand-drawn graphs depicting dynamics of student conversations were created (n = 3). In the final iteration, talk-turns were recorded in a table format along with notes (n = 4). Each talk-turn was either a question (“q”) or response (“r”).
The third and final iteration combined both the earlier iterations and also recorded the order of talk-turns. In addition to the hand-drawn diagrams for physical positions, talk-turn data were recorded in a question-or-response format in a spreadsheet, and qualitative notes and memos were written during observations. Each participant was assigned a number based on the initial order in which he or she first talked in the group. Whenever a participant talked, his or her number was recorded under either the question or response column, which resulted in directed data for our graph theory calculations. For the purpose of this study, questions were nonrhetorical (Smith et al., 2013), and responses were defined as utterances that did not contain a question. While we acknowledge that group discussions have complex discourse patterns not captured in this simple format, we wanted to include discourse moves as part of the methodology, so future studies can examine group discussions by combining quality discourse data and our quantitative methodology.
General Behaviors
We examined how many questions and responses were provided by each participant (peer facilitator and students) in a group. Questions and responses per hour were calculated using the following formulas, and scatter plots were generated to visualize the talk patterns of participants. These plots especially allowed us to compare the behaviors of peer facilitator versus students within a group.


For comparisons across groups, a normalized talk ratio was calculated based on a fair-share number of turns for each participant, assuming that all participants in the group talked for an equal number of turns. Normalized talk ratio for a given participant was then calculated as the number of talk-turns by that participant divided by the fair-share number of turns in the group.


A participant who talked more than his or her fair share of turns would have a normalized talk ratio of >1.0, whereas a participant who talked less than his or her fair share of turns would have a normalized talk ratio of <1.0, regardless of the size of the group.
Episode Length
From our third iteration of data collection with the question-and-response format, we defined an episode in the discussion as the number of talk-turns from a question to the last response immediately before the next question. We reasoned that a question was likely to indicate a new episode, especially in the initiation–reply–evaluation discourse pattern typically observed in a classroom (Macbeth, 2003), while acknowledging that many other scenarios may also occur, for example, a non sequitur response that leads to a new and productive direction (or episode) of the discussion. Nonetheless, we wanted to establish and test a robust methodology that can handle episodes, a common feature in discourse analysis, for potential future studies. With this operationalized definition of episodes, we calculated the frequency of episodes in different lengths.
Graph Theory Parameters
Data were processed and analyzed using a combination of Microsoft Excel (Microsoft Corporation, 2016), NodeXL Basic (Smith et al., 2010), MATLAB (Mathworks, 2017), and R (R Core Team, 2017). For analysis in NodeXL Basic, data in the question-or-response format were converted into an edge list, which included participant pairs who engaged in talk-turns, with corresponding weights for each of the edges. Subgroups were identified using the Girvan–Newman algorithm, a hierarchical method designed for small groups (Girvan and Newman, 2002). To automate data processing and to make data analysis more transparent, we developed custom scripts in MATLAB and R. Our MATLAB script takes the talk-turn data in the question-and-response format and generates an edge list and a corresponding weight list for the edges. These two lists serve as inputs for our R script, which uses the igraph package to calculate graph theory parameters that we define in the Methodological Framework section (Kolaczyk and Csardi, 2014). All scripts and the source code (at the time of publication) are available online in the Supplemental Material.
Case Study Selection
We use a case study approach to highlight the potential utility of our methodology. Case studies are especially useful for two purposes: 1) to examine the range and variations that exist within a setting and 2) to probe particular instances that are problematic or unusual (Case and Light, 2011). As such, the strength and value of case studies are not about generalizability; rather, case studies can provide insights as exemplars (Flyvbjerg, 2006). Here, we selected three case studies that demonstrate outcomes in group dynamics that could be observed using our methodology. Two cases were selected to contrast the extremes of talk-turn behaviors observed in discussions, and a third case was selected to highlight the existence of hidden subgroups.
RESULTS
Talk-Turn Behaviors in Groups
We used the question-and-response data to examine at the talk-turn behaviors of individual participants in groups, comparing peer facilitators with students and students with one another. From the four groups observed in this iteration of data collection, we identified two extreme patterns (Figure 5). First, using the question and response per hour data, we found that the peer facilitators in groups A and B were nearly indistinguishable from students in their respective groups (Figure 5, first row). In these groups, the peer facilitators and students engaged in similar number question turns and response turns. For example, in group A, the peer facilitator had 17.3 question turns and 88.0 response turns per hour, compared with 13.3 question turns and 80.7 response turns per hour for the next most active person in the group. On the other hand, in groups C and D, the peer facilitators had distinct behaviors compared with students. These peer facilitators engaged in many more talk-turns compared with students in their groups and also had more question turns per hour compared with the peer facilitators in groups A and B. For example, in group D, the peer facilitator had 141.3 question turns and 120.0 response turns per hour, compared with 14.7 question turns and 73.3 response turns per hour for the next most active person in the group.
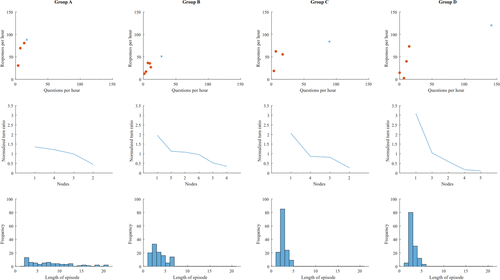
FIGURE 5. Characteristics of individual and group talk-turn behaviors. In the first row, questions and responses per hour are shown in scatter plots. Each point represents a student in the group, with the peer facilitator indicated by “X.” Four groups (A–D) are arranged based on the average distance of each student from the peer facilitator in the scatter plot to highlight peer facilitator talk behaviors in comparison to student talk behaviors. In the second row, normalized talk-turn ratios are plotted in descending order for each individual in the group, with Person 1 being the peer facilitator. Individuals are numbered based on the order in which they first talked. In the third row, histograms represent the distribution of episodes in one recorded session for each group. For the purpose of this study, episodes are defined as the number of talk-turns in between two questions.
To compare across groups more easily, we used the normalized talk ratio defined in the Methods section (Figure 5, second row). Consistent with the question and response per hour data, the peer facilitator in group A had a normalized talk ratio of 1.36, closest to 1 out of all the peer facilitators. In contrast, the peer facilitator in group D had a normalized talk ratio of 3.08, highest among the groups. Group A also had the smallest variation in normalized talk ratios among all participants (SD = 0.40, max = 1.36, min = 0.45, range = 0.91). Group B had a similar variation in normalized talk ratios (SD = 0.57, max = 1.96, min = 0.35, range = 1.61). On the other end of the spectrum, group D had the largest variation in normalized talk ratios (SD = 1.22, max = 3.08, min = 0.11, range = 2.97), followed by group C (SD = 0.75, max = 2.05, min = 0.27, range = 1.79). Within each individual group, the peer facilitators had the highest normalized talk ratios. Across groups, we can infer that, in groups A and B, the peer facilitators behaved similarly to the students, whereas in groups C and D, the peer facilitator behaved more like a traditional classroom authority figure.
Groups A and B had longer episode lengths and fewer total number of episodes compared with groups C and D (Figure 5, third row). In one extreme, group A had episodes ranging from 2 to 20 talk-turns, with an average of 4.85 episodes per hour; on the other hand, group D had episodes ranging from 1 to 5 talk-turns, with an average of 3.26 episodes per hour. Groups A and B also had lower proportions of episodes with 2 talk-turns at 20 and 30%, respectively, compared with groups C and D, with 61 and 62%, respectively. We found that episode lengths tended to be longer in groups in which the peer facilitators and students had similar talk-turn behaviors.
Graph Theory Analysis
To demonstrate the potential utility of our methodology, we present three case studies highlighting a decentralized graph, a centralized graph, and a graph with subgroups (Figure 6 and Table 2). Case 1 (Figure 5, group A) is a decentralized graph containing four nodes, with a majority male peer facilitator (node 1), two majority female students (nodes 3 and 4), and one underrepresented minority (URM) male student (node 2), seated physically in a circular format similar to that of a roundtable (Figure 6, left). The graph has a total of 12 edges, resulting in a density of 1.00; that is, all possible pairs of participants engaged in at least 1 talk-turn between them. The peer facilitator has a degree centrality value of 6.00, and the network has a centralization value of 0.00, meaning that no one participant is the majority speaker in the group. The two female participants talked for 55% of turns, and the two male participants talked for 45% of the turns; both percentages are near 50% of the fair share between genders based on the number of participants. The one URM participant talked for 11% of the turns, lower than the 25% of the fair share based on ethnicity.
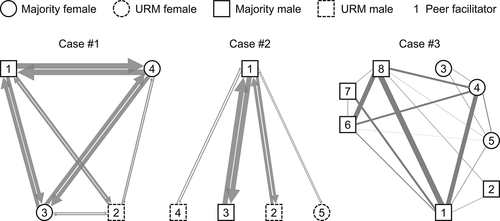
FIGURE 6. Three cases analyzed by our graph theory methodology. In these graphs, each individual and his or her demographics are presented as a node. Transitions between talk-turns are represented by arrows, and the arrow thickness indicates the cumulative number of transitions. At one extreme, case 1 is a decentralized group in which the peer facilitator (Person 1) appears to be nearly indistinguishable from students. At the other extreme, case 2 is a centralized group in which the peer facilitator dominates the talk-turns. Case 3 is an intermediate case that also highlights the existence of subgroups, which are divided between the two genders. Note that case 3 is undirected compared with cases 1 and 2, which are directed.
| Parameter | Case 1: Decentralized | Case 2: Centralized | Case 3: Intermediate |
|---|---|---|---|
| Nodes | 4 | 5 | 8 |
| Edges | 12 | 8 | 17 |
| Density | 1.00 | 0.40 | 0.61 |
| Centrality (peer facilitator) | 6 | 8 | 6 |
| Centralization | 0.00 | 1.00 | 0.33 |
| Subgroups | None | None | 2 |
Case 2 (Figure 5, group D) is a centralized graph containing five nodes, with a majority male peer facilitator (node 1), one minority female student (node 5), and three URM male students (nodes 2, 3, and 4), seated physically in a more traditional classroom format with the peer facilitator at the front (Figure 6, middle). The graph has a total of eight edges, resulting in a density of 0.40; that is, not all participants engaged in talk-turns with others in the group. The peer facilitator has a degree centrality value of 8.00, and the network has a centralization value of 1.00, meaning that one participant (the peer facilitator) is the majority speaker in the group. The five male participants (including the peer facilitator) talked for an overwhelming 98% of the turns, whereas the female minority student talked for only 2% of the conversation; these percentages are in stark contrast to the fair-share percentages of 80 and 20% for males and females, respectively. The three URM students talked for 18% of the turns, much lower than the 60% of their fair share based on ethnicity.
Case 3 is a larger group with an intermediate pattern between the two extremes. This graph contains eight nodes: a male peer facilitator (node 1), three female participants (nodes 3, 4, and 5), and four male participants (nodes 2, 6, 7, and 8), seated physically in a circular format (Figure 6, right). The graph has a total of 17 edges, resulting in a density of 0.61. The peer facilitator has a degree centrality of 6.00, and the network has a centralization value of 0.33. The peer facilitator talked for 28% of the turns (compared with fair share of 12.5%); the three female participants talked for only 24% of the turns (compared with fair share of 37.5%), whereas the four male participants talked for 47% of the turns (compared with fair–share of 50%). Most interestingly, two subgroups were identified using the Girvan–Newman algorithm (Girvan and Newman, 2002), even though they may not be immediately obvious from visual inspection of the graph itself. These two subgroups were divided by gender, with one subgroup consisting of the female participants and the other subgroup the male participants, suggesting that participants of the same gender were more likely to talk before and after one another.
DISCUSSION
In this study, we adapted graph theory as a methodology to examine the dynamics of discussions by tracking the turns in which students talk in small groups. In our peer-led groups, we identified two major patterns: one in which the peer facilitator and students contribute to the discussion relatively evenly and another in which the peer facilitator behaves more like a classroom authority figure. Furthermore, in one of our large groups, we observed subgroups divided along gender lines. Our data are consistent with patterns described in previous studies in the existing literature, demonstrating the utility and validity of our methodology.
In the groups in which the peer facilitator and students had similar behaviors, we observed higher episode lengths and lower ranges of the normalized talk ratios, lower centralization values, and higher graph densities, all indicators of fairly equal division of labor. These observations are consistent with the peer facilitators guiding discussions to help students build conceptual understanding (Eberlein et al., 2008; Micari et al., 2010; Pazos et al., 2010). In contrast, in the groups in which the peer facilitator behaved more like an authority figure, we observed shorter episodes (especially with length = 2), greater ranges of normalized talk ratios, higher centralization values, and lower graph densities. The high proportion of episodes with length = 2 is consistent with the peer facilitators providing directed instruction in the inquiry–response–evaluation discourse pattern typically observed in a classroom (Macbeth, 2003; Micari et al., 2010; Pazos et al., 2010), which is not necessarily aligned with the tenets of social constructivism.
Our data suggest that seating arrangements can be correlated with how participants engage in discussion. For example, in case 1, students were seated in a circular format facing one another, and the resultant graph has a high density, indicating that students engaged in talk-turns with one another. In case 2, students were seated in a more traditional classroom structure facing the peer facilitator at the front, and the resultant graph has a low density. These observations suggest that physical arrangements of the classroom (i.e., the tools in CHAT) can influence how different people engage with the activity. These observations are consistent with existing literature: Students in circular seating are more likely able to maximize group interactions; in contrast, the typical classroom seating with students facing the front tends to emphasize the role of the instructor (or peer facilitator) and minimize student–student interactions (McCorskey and McVetta, 1978; Wannarka and Ruhl, 2008; Borgatti et al., 2009).
We observed some important patterns related to equity and inclusion in groups, again consistent with existing literature. For example, in case 3, two subgroups were identified using graph theory methods, and the subgroups were divided by gender, suggesting that there are additional hidden social rules within the group that are guiding or informing the talk patterns among students. In case 2, there was only one female participant, and she had the lowest talk-turn contribution out of all the participants. In contrast, case 1 had an equal number of female and male participants, and talk-turn contributions were even across the two genders. According to the existing literature, groups with gender balance result in females having a slightly greater influence and relatively equal achievement across genders, whereas when females in a group are in the minority, they tend to have less influence and lower achievement than males (Strodtbeck and Mann, 1956; Webb, 1982a, 1984; Craig and Sherif, 1986). Another important pattern we noticed is in the number of talk-turn contributions of URM students. In both cases 1 and 2, majority students in the group had higher percentages of talk-turn contributions compared with URM students. Our results are also in line with previous research: URM students are more likely to face intimidation and experience social-comparison effects (Micari and Drane, 2011) and tend to have fewer interactions within groups (Cohen and Roper, 1972).
Our methodology can serve as an important tool to understand and assess how students participate and engage in group discussions. One potential application is observing the effects of how different combinations of demographics may affect student participation, and this information can then be used to inform how instructors can create more equitable classrooms for all students to engage in meaningful learning. Second, we can use this methodology to examine the effects of class structure on student participation; these could include physical structures such as spatial seating of the classroom and pedagogical structures such as instructor talk (Seidel et al., 2015). Furthermore, information about student participation can be captured at various time points throughout an academic term to determine the progression for how groups may coalesce over time to create more effective collaboration. For assessment purposes, this methodology can provide a means for instructors to quantify contribution by individual members in a group and provide feedback to students. Ultimately, quantitative information obtained from this methodology can be used to help students learn to collaborate and inform instructors on how to moderate discussions.
Limitations of the Study
Our study has a few limitations. First, we had a limited number of groups in our final iteration of data collection and analysis, so we were not able to make generalizable conclusions. However, our goal was simply to establish a quantitative methodology based on graph theory to examine student discussions in small groups. Even from our limited data set, we were able to observe patterns consistent with various observations the existing literature, indicating the validity of our methodology.
Second, our methodology does not consider whether an individual is addressing the entire group or a specific person. In a group, when an individual speaks, everyone else can be listening. However, it is simply not feasible to determine whether each person in the group is listening or not. Furthermore, it is not practical to model this kind of listening information using graph theory. Assuming that everyone is listening, the resultant graph will have edges from the speaker node to all other nodes. Essentially, the graph will be saturated with edges and will likely not provide any useful information. Our methodology tracks the talk-turn behavior of individuals in a group, which can tell us much more about the dynamics of the discussion.
Third, our methodology tracks only the sequential order of talk-turns and not the content of discussion. One solution to this problem is combining our graph-theory methodology with discourse analysis to incorporate the substance of the discussion into our mathematical model. We had intentionally developed the methodology with this purpose in mind; for example, including discourse moves and episodes in the data processing and analysis pipeline. As such, our methodology should be robust enough to handle different kinds of data, including clicker discussions, group work in laboratory setting, and various small-group learning environments such as problem-based learning, peer-led team learning, and process-oriented guided-inquiry learning.
Some quantitative methods currently exist to analyze patterns of group discussions. For example, a computer-based method has been used to map the content of the conversation to show how participants contribute in the group and to understand how group dynamics can affect learning outcomes (Barros and Felisa Verdejo, 2000). Our methodology complements this existing work. We tracked how participants engage in talk-turns, while the previous study focused on how the content of the discussion and the types of contributions may affect learning outcomes (Barros and Felisa Verdejo, 2000).
Despite these limitations, our methodology can serve as an important tool in examining and understanding group work by capturing the dynamics of how students engage in talk-turns in the discussion (Figure 1). We observed some interesting and important patterns, such as centralized versus decentralized groups, potential effects of seating arrangements on talk-turn behaviors, and influence of gender and minority status in group contributions, all of which are consistent with other observations in the existing literature. With this methodology, we will be able to examine how various student characteristics may influence group dynamics in discussions and how differences in talk-turn behaviors may contribute to the success of student outcomes.
ACKNOWLEDGMENTS
We are grateful to the students and peer facilitators who participated in this study. We thank G. Light, C. Mamas, and M. Micari for early discussions on the project. This work was supported in part by the Faculty Career Development Program (SML) at the University of California, San Diego. A.C. was an undergraduate researcher in the Faculty Mentor Program at the University of California, San Diego.