Molecular Thermodynamics for Cell Biology as Taught with Boxes
Abstract
Thermodynamic principles are basic to an understanding of the complex fluxes of energy and information required to keep cells alive. These microscopic machines are nonequilibrium systems at the micron scale that are maintained in pseudo-steady-state conditions by very sophisticated processes. Therefore, several nonstandard concepts need to be taught to rationalize why these very ordered systems proliferate actively all over our planet in seeming contradiction to the second law of thermodynamics. We propose a model consisting of boxes with different shapes that contain small balls that are in constant motion due to a stream of air blowing from below. This is a simple macroscopic system that can be easily visualized by students and that can be understood as mimicking the behavior of a set of molecules exchanging energy. With such boxes, the basic concepts of entropy, enthalpy, and free energy can be taught while reinforcing a molecular understanding of the concepts and stressing the stochastic nature of the thermodynamic laws. In addition, time-related concepts, such as reaction rates and activation energy, can be readily visualized. Moreover, the boxes provide an intuitive way to introduce the role in cellular organization of “information” and Maxwell's demons operating under nonequilibrium conditions.
INTRODUCTION
Education in the broad and complex field of biology needs to be founded on some core concepts (Klymkowsky, 2010). Cells are the basic units of life; hence, how cells work and the molecular mechanisms involved in cell physiology are an essential part of the curricula of all undergraduate programs in the biological sciences. As we understand them, cells are incredibly sophisticated, self-sufficient, microscopic “machines.” Despite their complexity, cells are governed by the same principles that apply to all physicochemical systems. Specifically, they handle energy in the same way that macroscopic machines do. Therefore, basic concepts of thermodynamics are essential to an understanding of the molecular mechanisms underlying all cell functions (Klymkowsky, 2010). Although a qualitative understanding would be sufficient for most biology students, the relevant thermodynamic principles are not the standard ones that apply to simple thermal engines. Cells are nonequilibrium systems in which information plays an essential role. Therefore, several nonstandard concepts need to be taught to explain why these very ordered systems proliferate actively all over our planet despite their apparent disregard of the second law of thermodynamics.
Most biology students are acquainted with molecules. They think about proteins (antibodies, receptors, enzymes), lipids (phospholipids, cholesterol, triglycerides), and other biological molecules as real entities. In contrast, entropy, enthalpy, and free energy are abstract concepts that students can learn to express in an equation and use to get a result without really grasping the important concepts. And as soon as they forget the formula, they are likely to forget most of the underlying thermodynamic principles, except that energy is somehow important. Students would almost certainly incorporate these concepts more readily if they had an intuitive idea of the molecular basis of the laws of thermodynamics. However, the formal means of connecting molecules and thermodynamics is statistical mechanics, which is mathematically challenging for many biology students, especially as it applies to nonequilibrium situations.
MOLECULAR THERMODYNAMICS IN A BOX
The goal is to teach the thermodynamic concepts necessary for understanding how cells handle energy, while keeping mathematics to a level accessible to the students. A useful strategy for this is to work with a simple macroscopic system that can be readily visualized by the students and that behaves as a set of molecules exchanging energy during a process.
The idea presented here is an extension of the boxes used in the cell biology textbook The World of the Cell (Becker et al., 2008). The analogy was first developed by Harold F. Blum in the book Time's Arrow and Evolution (1968). The strategy is to picture a box containing small balls that are in constant movement due to a stream of air blowing from below (Figure 1). This device is analogous to the “lottery ball picker” machines frequently used for random selection of numbers in several television shows. The collisions of balls against the box walls and against one another are not elastic; hence, if the airstream is turned off, the balls will rapidly lose energy and come to rest on the floor of the box. In the four boxes in Figure 1, the stream of air is blowing with increasing strength from left to right. In this system, we can think of balls as molecules having different levels of energy following a Boltzmann distribution. The airstream, which provides the energy that propels the balls upward in the box, is equivalent to the absolute temperature in the Boltzmann distribution. The higher the temperature, the more kinetic energy the molecules in the system will have. The important concept is that the number of molecules at different energy levels (i.e., different distances from the floor) follows a Boltzmann distribution. Students can easily and intuitively visualize balls with different energy levels without any mathematical deduction. The influence of the temperature in this distribution is also very intuitive. To reinforce the box image, a simulation was programmed in Visual Basic as a macro in an Excel worksheet (Supplemental Material). A movie generated with this simulation shows that the distribution of the balls in the box is dynamic and changes with temperature (see Movie S1 in the Supplemental Material).
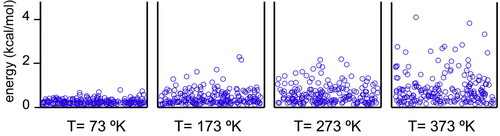
Figure 1. Boltzmann distribution illustrated in a box. Two hundred balls were distributed in a two-dimensional box according to the following rules: For each ball, the x position was randomly selected within the limits of the box. The y coordinate (energy) was randomly selected as y = −R · T · ln(Rnd), where R is 1.986 cal K−1 mol−1, T is the absolute temperature in degrees Kelvin, and Rnd is a random number in the 0–1 range. The distribution is shown for four different temperatures. The figure was generated using a simulation programmed in Visual Basic as a macro in an Excel worksheet (see Supplemental Material).
Now, if two sectors of the box are considered, the number of molecules in each sector depends on the area of each sector and on the floor level of the sector. These two factors accurately correspond to the entropy and the enthalpy difference between the two sectors (Figure 2). In this macroscopic system, both concepts are very easy to visualize. Also, the influence of temperature on the distribution of molecules can be intuitively inferred. In other words, students should be able to grasp the concept of free energy based on the distribution of balls in boxes with different shapes.
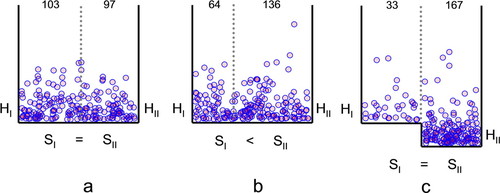
Figure 2. Differences in entropy and enthalpy shown in boxes. Two hundred balls were distributed in two-dimensional boxes divided into two sectors according to the following rules and considering an absolute temperature of 310 K. For each ball initially in sector I (or sector II), the y coordinate (energy) was randomly selected as y = Hi − R · T · ln(Rnd), where Hi is the floor level for the ball's sector (0 for sector I and ΔH for sector II) and Rnd is a random number in the 0–1 range. If the height of the y coordinate was higher than the energy step necessary to pass to the other sector, the x coordinate was randomly selected within the limits of the entire box, such that the wider sector received proportionally more balls. If the y coordinate was lower than the energy step, the x coordinate was randomly selected within the limits of the sector where the ball was located initially. The two sectors in box (a) have the same entropy and enthalpy. The left sector in box (b) has lower entropy than the right sector (ΔS = R · ln(0.666/0.333) = 1.3766 cal K−1 mol−1). The right sector in box (c) has lower enthalpy than the left sector (ΔH = −1 kcal mol−1). The number of balls in each sector is shown at the tops of the boxes. The figure was generated using a simulation programmed in Visual Basic as a macro in an Excel worksheet (see Supplemental Material).
Notice that the box analogy is quantitatively correct for a single-molecule reaction (e.g., 1-propanol ↔ 2-propanol in Figure 3A). For this reaction, the change in standard molar enthalpy (ΔH°) and entropy (ΔS°) are known (−3.63 kcal mol−1 and −3.85 cal mol−1 K−1, respectively [Stretton, 2005]). The box in Figure 3A was built considering ΔH° as the difference in floor levels. The size of both compartments in the box was calculated from the relationship between entropy and probability.
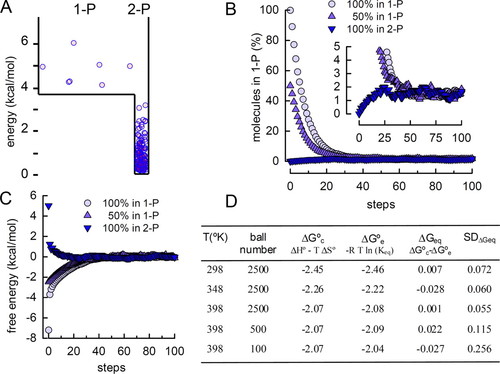
Figure 3. Teaching thermodynamic concepts with a box representing a real chemical reaction. (A) The 1-propanol ↔ 2-propanol reaction is represented in a box. The difference in floor levels corresponds to the change of standard molar enthalpy of the reaction (ΔH° = −3.63 kcal mol−1). The width of the right and left sectors corresponds to the ΔS° (−3.85 cal mol−1 K−1) and was calculated as explained in the section Molecular Thermodynamics in a Box. Two hundred balls were distributed in this box following the rules described in Figure 2, and the process was repeated until equilibrium was reached. (T = 298 K). (B) Using this box, simulations with 2500 balls were started with 2499 balls in sector I and one ball in sector II, or one ball in sector I and the rest in sector II, or 50% of the balls in each sector. The balls were redistributed 100 times; at each step, the number of balls in the 1-P and 2-P sectors of the previous step was used. The percentage of balls in the 1-P sector is plotted at each step. Inset, the 0–5% range was enlarged to show that all three conditions converge to 1.57%, corresponding to Keq = 62.79. (C) The numbers of balls in the two sectors, as shown in (B), were used to estimate the free energy of the system at different steps (see the section Molecular Thermodynamics in a Box for details in the calculation). Notice that ΔG approaches 0 independent of the initial conditions used. (D) The table shows the absolute temperature, total number of balls, and ΔG° calculated from the known temperature and the changes in entropy and enthalpy of the reaction. Simulations with these parameters were run, and Keq, ΔG°, and ΔG were estimated by averaging the values of the last 60 steps (where the simulations had reached equilibrium). The last column shows the SD during the last 60 steps.
ΔS = R · ln(p2/p1), where R is the gas constant (1.986 cal mol−1 K−1) and p1 and p2 are the relative width of the right and left compartments, respectively (notice that p1 + p2 = 1).
Hence, knowing ΔS°, the size of the left compartment can be calculated as: p1 = 1/[1 + exp(ΔS°/R)], and p2 = 1 − p1 (in Figure 3A, p1 = 0.875 and p2 = 0.125).
ΔG° depends only on the shape of the box and the absolute temperature (T), and it is calculated as ΔG °c = ΔH° − T·ΔS°,where “c” stands for calculated (Figure 3D). In contrast, ΔG depends also on the number of molecules in each sector.
ΔG = ΔG° + [R · T · ln(M2/M1)], where M2 and M1 are the number of balls in the right and left compartments, respectively.
When students start simulations with this box, ΔG can be negative or positive at the beginning, according to the number of balls initially allocated in each sector (Figure 3, B and C). As the simulation progresses, ΔG approaches 0 and the system reaches equilibrium (the number of balls moving forward equals the number of balls moving backward; Figure 3C). At this stage, M2/M1 fluctuates around the equilibrium constant (Keq; inset in Figure 3B). Keq, like ΔG°, depends only on the temperature and the box shape. In fact, students can “experimentally” calculate ΔG° from Keq and confirm that it matches the “calculated” value (Figure 3D): 
Students can use the simulation to quantitatively explore the effect of temperature on the equilibrium constant and ΔG° (Figure 3D). The stochastic nature of the laws of thermodynamics is also evident in all these simulations and can be visualized by changing the number of balls in the box. The fluctuation of ΔG at equilibrium increases as the number of molecules in the simulation decreases (Figure 3D).
CHEMICAL REACTION KINETICS IN A BOX
Instructors can also use boxes to introduce time-related concepts in chemical reactions. A barrier can be built between the two sectors (Figure 4A), such that only balls jumping higher than the barrier can pass to the other sector. This wall accurately represents the activation energy in a chemical reaction. Students can be prompted to start simulations with all of the balls in one sector and to follow the kinetics of transfer to the other compartment in boxes having different activation energies. This strategy is a useful means of introducing the concept of reaction rate and the influence of activation energy. It also shows that the activation energy does not affect the equilibrium constant (Figure 4B and Movie S2 in the Supplemental Material).
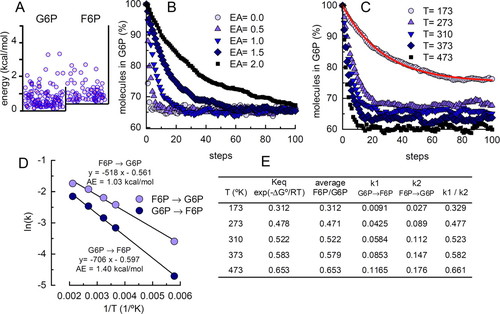
Figure 4. Teaching chemical reaction kinetics with a box. (A) The box represents the glucose-6-phosphate (G6P) ↔ fructose-6-phosphate (F6P) reaction with activation energy = 1 kcal mol−1. The experimental ΔG° for this reaction is 0.4 kcal mol−1. The box was drawn assuming that the ΔS for the reaction is close to 0 and ΔH = 0.4 kcal mol−1. Two hundred balls were distributed in this box following the rules described in Figure 2, and the process was repeated until equilibrium was reached (T = 298 K). (B) Using this box, simulations with different activation energies were initiated with all the balls in the G6P sector (hence, initial rates correspond to the forward reaction). The balls were redistributed 100 times; at each step, the number of balls in the G6P and F6P sectors of the previous step was used. The percentage of balls in the G6P sector is plotted at each step. (C) Simulations at different temperatures, using the same box and conditions described in (B) with an activation energy = 1 kcal mol−1. The red curve was adjusted to the simulation values for T = 473 K, modeling the reaction in COPASI and using the Parameter estimation module (Hoops et al., 2006). (D) Simulations shown in (C) were used to estimate kinetic constants for the forward and backward reactions, as described in (C). These constants were used in an Arrhenius plot to estimate activation energies for the forward and backward reactions. Notice that the estimated activation energies are close to those shown for the box in (A): 1 kcal mol−1 above the 0.4 kcal mol−1 of the ΔH step for the G6P → F6P reaction and 1 kcal mol−1 for the backward reaction. (E) A table that compares the equilibrium constants calculated from the free energy of the reaction with the equilibrium constants obtained from the simulations in (C), averaging the last 20 values and from the kinetic constants of the reaction estimated in (C).
Students can quantitatively explore the effect of temperature on the reaction kinetics using the simulation (Figure 4C and Movie S3 in the Supplemental Material). The changes in the proportion of molecules in the two compartments as the simulation progresses follow reversible, first-order reaction kinetics. The kinetic constant for the forward reaction is obtained graphically from the initial rates in simulations, as shown in Figure 4B. More accurate estimates are easily obtained by using available software. For example, an a ↔ b reaction was modeled in COPASI (www.copasi.org), and the parameter estimation routine was used to adjust the values obtained in the simulation to the differential equation dM1/dt = (−k1 · M1) + (k2 · M2), where k1 and k2 are the forward and backward kinetic constants, respectively; t is the time variable measured in steps (Figure 4, C and E).
Students can use the kinetic constants for the forward and backward reactions at different temperatures to calculate the activation energy in an Arrhenius plot (Figure 4D) or to calculate the equilibrium constant of the reaction (Figure 4E).
THERMODYNAMICS FOR CELL BIOLOGY IN A BOX
The thermodynamic concepts introduced with boxes in the previous sections are sufficient for describing most physicochemical systems, but some additional concepts are required for understanding cell function. Cells are open systems operating under nonequilibrium conditions. Moreover, information plays a central role in the behavior of these small machines. Boxes are also valuable as a means of introducing these concepts.
With boxes, the molecular level of understanding is never lost, so nonequilibrium conditions are easily visualized. Students can readily understand the necessity of driving an energy-requiring reaction (this is a reaction with a positive ΔG value) by coupling it to a reaction that releases energy. For example, if the synthesis of glucose-6-phosphate from glucose and inorganic phosphate with a ΔG° = +3.3 kcal mol−1 is modeled in the box simulation, it is evident that very little product can be obtained, and this cannot be changed by manipulating the activation energy of the reaction (Figure 5A). On the other hand, the box of the synthesis of glucose-6-phosphate using glucose and ATP, with a ΔG° = −3.7 kcal mol−1, has a clear tendency to form the product (Figure 5B). An enzyme lowering the activation energy of this reaction would control the synthesis of glucose-6-phosphate. Students can play with a three-compartment box representing the two reactions and can analyze the glucose metabolism in cells having different sets of enzymes for catalyzing these reactions (Figure 5C). The key concept that enzymes function by decreasing activation energy as a means of guiding molecules through the required metabolic pathways can be visualized and incorporated as a foundational concept in cell biology by using boxes with several compartments isolated by large energy barriers.
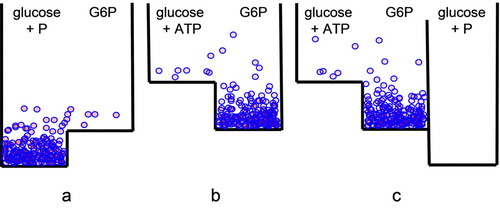
Figure 5. Boxes qualitatively representing the reaction of glucose phosphorylation from (A) inorganic phosphate or (B) ATP are shown. (C) A three-compartment box symbolizing the basic strategy for the synthesis of glucose-6-phosphate (G6P) in the cell.
According to Clausius' interpretation of the second law of thermodynamics, isolated systems spontaneously result in an increase in entropy, which is generally associated with disorder. Most people find it hard to understand that this law is compatible with the existence of cells, which are highly ordered systems. The explanation generally used is that every spontaneous process results in an increase in total entropy—that is, the entropy of the universe—and that thermodynamics therefore does not deny the possibility that a part of the system may become highly ordered if the rest of the system undergoes an increase of entropy that compensates for the local decrease in the ordered sector. Although valid, this statement tends not to satisfy students, who would like thermodynamics to provide a more convincing framework explaining why living organisms are so abundant in our world. For this, the concept of information must be introduced. The relationship between information and energy is key to understanding biological systems (Schneider, 2010).
Maxwell's thought experiment is a convenient way to introduce information in a thermodynamic context (Maroney, 2009). Starting with a box with two identical sectors having initially the same number of balls, the system will progress to an uneven distribution if a “demon” can decrease the energy barrier only when balls are coming from the left compartment. This process seems to violate the second law of thermodynamics. The initial state has higher entropy than the final one. This paradox is solved by assuming that the demon has information: It could distinguish molecules coming from the left from molecules coming from the right. The energy required to obtain and use the information preserves the validity of the second law (Schneider, 2010). The system has moved to the higher probability state in the presence of a demon with the necessary information. Students can learn about the power and limitations of a demon to manipulate the entropy of a two-compartment box by exploring the excellent interactive simulation modeled by Criado and López (2004). In this simulation, the physical properties of the demon and the information that it handles can be controlled.
Instructors can use DNA synthesis to introduce the central role of information in cell biology. Building a DNA strand from deoxynucleoside triphosphates is energetically favorable. However, students are well aware that the cell must synthesize a very specific DNA—that is, a DNA molecule with a unique sequence of nucleotides. The total number of different combinations for a small piece of DNA having 600 nucleotides is 4600 = 10360. The representation for the synthesis of DNA should be a box like the one shown in Figure 6. The left sector represents the 10360 − 1 incorrect combinations, and the one on the right represents the single correct combination (DNA*). The cell uses a DNA polymerase, which behaves as a Maxwell's demon (operating under nonequilibrium conditions), to solve this problem and synthesize the DNA strand with the required nucleotide combination. The addition of a nucleotide to the growing strand has high activation energy; hence, it will not occur unless an enzyme can decrease this barrier. The DNA polymerase will only catalyze the incorporation of a new nucleotide if it matches the template strand, which contains the information used by the demon. So, from the 10360 possible combinations, the polymerase will only decrease the activation energy for the synthesis of the complementary strand. The synthesis of all other possible chains is prevented by the large activation energy. In brief, the DNA polymerase reads the information coded in the template strand as a means of decreasing the activation energy of only the complementary deoxynucleotide to be incorporated into the growing strand. The student can identify real molecules that behave as Maxwell's demons, limiting the possible outcomes of a process and maintaining the high degree of organization required for the cell.
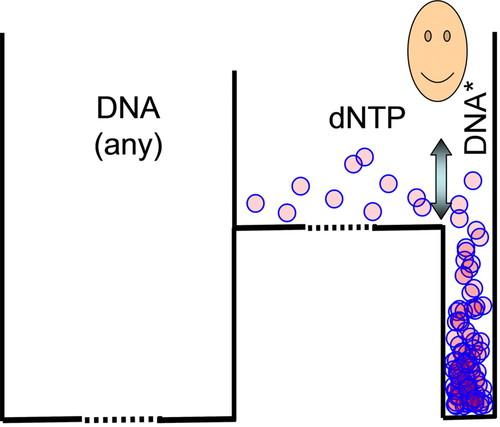
Figure 6. A box qualitatively representing the DNA synthesis reaction is shown. This three-compartment box introduces a Maxwell's demon that, by using the information in the template strand, decreases the activation energy only when the correct deoxynucleotide (dNTP) is incorporated into the enzymatic complex. The information limits the outcome of the reaction to a unique nucleotide sequence (DNA*). The discontinuous lines in the box floor symbolize the large entropy differences between random DNA sequences or free deoxynucleotides and the unique DNA strand synthesized.
USE OF BOXES IN AN UNDERGRADUATE COURSE
Balls in a Box can in principle be used in different courses and as a means of intuitively introducing thermodynamic principles to students at different levels. As an example, we present the results of using this approach in an introductory bioenergetics class for first-year students at the School of Medicine of the National University of Cuyo, Mendoza, Argentina. The design of the tests and the results reported were approved by the Medical Education Committee of the School of Medicine. The data collection of past examinations was performed according to the regulations of the School of Medicine. The pretest was a voluntary activity for students, who were informed that the test was part of this research, and the posttest was part of the regular activities of the course. The identity of the students was preserved in all tests.
Students came directly from high schools. They had very little background in thermodynamics. However, to be admitted into the medical school, a student must attend a course and pass a chemistry exam that includes the topics of chemical equilibrium and reaction rates. Since only about 15% of the students are selected (120 out of 800 applicants), the students are well-trained in these subjects. The class on bioenergetics is part of a 16-wk intensive course in biochemistry and cell biology. The 60-min class is complemented by a small-group exercise (20 students) that requires about 30 min to be completed. The material provided to the students is included here as Supplemental Material (Bioenergetics; see also Box 1). The results shown were collected from three final examinations (2009–2011), each of which included a question about bioenergetics that was one of a total of 50 questions. As shown in Figure 7, a large percentage of the students answered the questions satisfactorily. Moreover, bioenergetics was not a particularly difficult subject for the students. When the 50 questions were ordered according to the average score obtained, thermodynamics ranked in the 18th, 10th, and 15th place for the 2009, 2010, and 2011 exams, respectively.
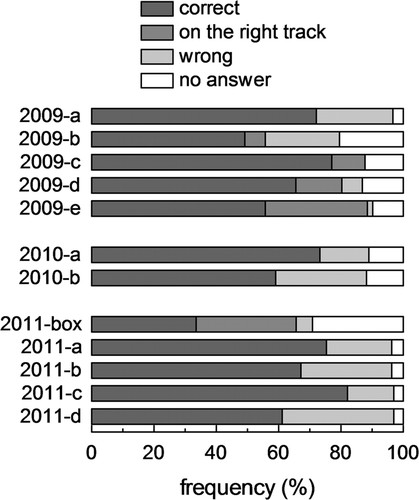
Figure 7. Scores for bioenergetics questions in final examinations of a biochemistry and cell biology course for medical students. The tests had one question (from a total of 50) about bioenergetics. Each question consisted of several items that were evaluated separately. The answers were classified as “correct” (showed that the student understood the concepts required for the item), “wrong” (failed to show that the student understood the concepts required for the item), “on the right track” (showed that the students understood some concepts but not all that were required for the item), or “no answer” (empty space). Shown are the percentages in each category in the 2009, 2010, and 2011 exams (122, 127, and 134 students, respectively). English translations of the questions and an example for the classification of answers for one specific question (2011-box) can be found in the Supplemental Material.
Box 1. Suggested design for a bioenergetics course employing Balls in a Box
Introduce thermodynamic laws based on two intuitive concepts that are familiar to most students: energy and probability.
Present boxes as a way to represent a set of molecules having energies distributed according to a Boltzmann distribution. Divide the box in two and explain where enthalpy and entropy are represented in the shape of the box. Students can use the simulation to assess the effect of temperature and box shape on the final distribution of balls in the two sectors
Introduce the concepts of standard free energy, free energy, and equilibrium constant using boxes filled with different numbers of balls in each sector and allowing the molecules to reach equilibrium. This simulation is a very useful means of “experimentally” testing these concepts.
Introduce reaction kinetics by assessing the rate of transfer of balls between the two sectors. The representation of activation energy as a barrier between the sectors is very intuitive. Introduce the concept of enzymes as regulators of the activation energy. Use the simulation for “experimentally” testing many aspects of these concepts.
At this point, present the special challenges that energy and probability represent for biological systems. Use boxes with multiple compartments to show how enzymes guide the flow of reactions along the metabolic pathways by lowering the activation energies. Multicompartment box simulations have not yet been programmed; however, the use of boxes as a means of qualitatively representing different pathways is still useful.
Finally, introduce the role of information in living organisms by using the classical two-compartment thought experiment of Maxwell. Use DNA synthesis as a means of introducing information concepts to a biological system. DNA polymerase is an enzyme that students know well, and it is easy to show how it works as a Maxwell demon that uses the information in the template strand to guide the synthesis of a unique DNA molecule.
To assess whether the Balls in a Box approach could improve understanding of a subject the student had previously learned, a pre/posttest was administered that was limited to chemical equilibrium and reaction rates. It is worth noting that the bioenergetics class was not focused on these subjects, since it covered broader aspects of thermodynamics in biological systems. For the test, similar questions were asked before and after the class as part of a weekly quiz (see Supplemental Material). As shown in Figure 8, most of the students improved their understanding, even in concepts that they had studied previously using other approaches. On average, they performed better in five out of eight questions, and they improved their overall score in the quiz (data not shown). However, in one aspect, the box representation was less helpful than the methods that had been used previously (Figure 8d). In the box, the effect of a rise of temperature in an endothermic or exothermic reaction is inferred by imaging the number of balls in each compartment when the temperature is modified. However, this concept was taught in the chemistry course with a still simpler (although less flexible) approach, in which heat is considered a reactant or a product for endothermic or exothermic reactions, respectively. The result of this pre/postassessment will be used to improve the bioenergetics class in future years by incorporating previous concepts learned with different approaches. In conclusion, even for a single class, which is not the best scenario to introduce an innovative representation for complex processes, the Balls in a Box approach was an effective method to teach critical concepts about thermodynamics.
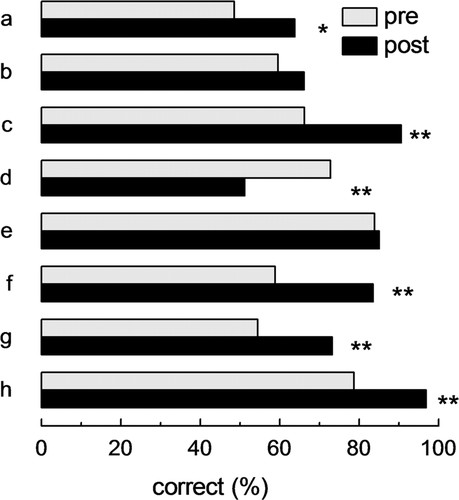
Figure 8. Pre/posttest to evaluate the box method as a means of teaching the topics of chemical equilibrium and reaction rate. Similar questions were asked before and after the bioenergetics class as part of the weekly quiz. The percentages of correct answers are shown in the pre/post quiz. The difference of pre/posttest answers for each question was compared using a Wilcoxon signed-rank test for paired observations (*, p < 0.05; **, p < 0.01). English translations of the questions can be found in the Supplemental Material.
CONCLUSIONS
Thermodynamics is a fundamental discipline that enables us to understand how energy is handled by living organisms. However, what students need to learn is by no means trivial; what is needed is a conceptual understanding of how nonequilibrium systems at the micron scale are maintained in pseudo-steady-state conditions by very sophisticated processes handling large amounts of energy and information. Many of the concepts are better understood by considering that the laws of thermodynamics are based on the stochastic behavior of large sets of molecules. Students (and most biologists at any level, for that matter) are used to thinking about molecules as the major players in most events in cellular and molecular biology. Boxes are useful as a means of applying thermodynamics to molecules without using statistical mechanics. Hence, it is a good way for students to incorporate concepts of thermodynamics into their “molecular world.” With boxes, the basic concepts of entropy, enthalpy, free energy, standard free energy, and activation energy can be taught while maintaining a connection with the behavior of individual molecules. A very nice simulation of balls interacting in a box that keeps track of the speed and kinetic energy of individual molecules is freely available (LeMaster, 2011). This simulation shows a more realistic view of molecules moving at different temperatures and can be used to complement the introduction of the boxes mimicking entropy/enthalpy differences.
Moreover, the boxes represent a very intuitive means of introducing nonequilibrium states and Maxwell's demons. Students are familiar with enzymatic complexes that are perfect examples of Maxwell's demons (e.g., DNA polymerase, RNA polymerase, ribosomes) and know much about how these demons work. Students can then easily grasp the concept of how information is used to guide a process to a final outcome that a priori would be predicted to be very unlikely.
In conclusion, we propose boxes as a very valuable strategy, especially when an intuitive framework of thermodynamics for biology must be taught in a short time. For more extended courses in bioenergetics, boxes may be useful tools to introduce some concepts and to simulate simple reactions, but then equations and real metabolic processes should be emphasized to ensure that students genuinely understand cell physiology. After all, balls bouncing in a box do not really represent all the complexity of the biochemical reactions required to maintain a cell.
ACKNOWLEDGMENTS
We thank Drs. Mario Estrada and Victor Pereyra (Universidad Nacional de San Luis, Argentina) for useful comments. This work was made possible thanks to the support of CONICET (Argentina), Universidad Nacional de Cuyo (Argentina), and the Alexander von Humboldt Foundation.