Improving Students’ Understanding of Biological Variation in Experimental Design and Analysis through a Short Model-Based Curricular Intervention
Abstract
When conducting biological investigations, experts constantly integrate their conceptual and quantitative understanding of variation with the design and analysis of the investigation. This process is difficult for students, because curricula often treat these concepts as separate components. This study describes the effect of a curricular intervention aimed at improving students’ conceptual and quantitative understanding of variation in the context of experimental design and analysis. A model-based intervention curriculum consisting of five short modules was implemented in an introductory biology laboratory course. All students received the regular laboratory curriculum, and half of the students also received the Intervention curriculum. Students’ understanding of variation was assessed using a published 16-question multiple-choice instrument designed and validated by the research team. Students were assessed before and after the intervention was implemented, and normalized gain scores were calculated. Students who received the intervention showed significantly higher normalized gains than students who did not receive the intervention. This effect was not influenced by students’ gender or exposure to prior statistics courses and persisted into and through the following semester’s laboratory course. These results provide support for the use of model-based approaches to improve students’ understanding of biological variation in experimental design and analysis.
INTRODUCTION
Experts constantly cycle between conceptual and quantitative modes of thinking when running biological investigations. They connect their knowledge about sources of variation with statistical concepts and then incorporate that understanding into the processes of experimental design and data analysis (Dasgupta et al., 2014; Altman and Krzywinski, 2015). The ability to integrate quantitative thinking into biological problems has been nationally prioritized as a core competency for undergraduate biology students (American Association for the Advancement of Science, 2011). However, the integration of conceptual and quantitative thinking can be difficult for students. Undergraduate students often have trouble identifying sources of variation and understanding how variation is represented in statistical expressions (delMas et al., 2007; Shtulman and Schulz, 2008). These difficulties can cause students to make incorrect attributions of the sources of variation in data they have collected and therefore misinterpret experimental results (Dasgupta et al., 2014).
One reason for the difficulties that students experience with integrating their conceptual and quantitative understanding of variation during biological investigations is that statistical concepts are not commonly integrated into most introductory biology laboratory courses (Metz, 2008; Colon-Berlilngeri and Burrowes, 2011). Curricula have been generated that aim to improve undergraduate students’ ability to design experiments (Dasgupta et al., 2014; Marsan et al., 2016), understand the role of variation in genetics or evolution (Bray Speth et al., 2014), or apply their statistical skills (Metz, 2008; Marsan et al., 2016). These curricular interventions tend to focus on improving students’ understanding in a specific area rather than making connections between conceptual understanding of sources of variation, quantitative expressions of variation, and biological investigations. We have previously described a curricular intervention (Biological Variation in Experimental Design and Analysis [BioVEDA] curriculum) designed for introductory undergraduate biology laboratory courses. The BioVEDA curriculum uses a model-based approach to enable students to identify sources of variation in an experiment, integrate that knowledge with statistical expressions of variation, and use their knowledge to inform experimental design and data analysis (Dewey et al., 2020). This current work describes the impact of that curriculum on students’ understanding of variation in the context of experimental design and analysis.
Biologists Integrate Conceptual and Quantitative Understanding of Variation
Variation is inherent to all biological investigations (Altman and Krzywinski, 2015). Understanding variation and how it impacts experimental design and analysis requires a complex merging of multiple ideas and perspectives. For example, in statistics, variation is often defined as “a measurement of the amount that data deviate from a measure of center, such as with the interquartile range or standard deviation” (Makar and Confrey, 2005, p. 28). In biology, understanding variation has been described as requiring the integration of a set of “interconnected processes including recognizing that phenotypic and genotypic variation exists within populations, that variation is inherited by offspring in units (i.e., alleles), and that gene expression changes over time (development) and is modulated by both temporal and spatial environmental variation” (Batzli et al., 2016, p. 3). When engaging in experimental design and data analysis, biology researchers must combine their understanding of the biological ideas about variation (conceptual) with their statistical ideas about variation (quantitative).
During the design phase of an investigation, a researcher must consider the sources of variation that may impact experimental outcomes (e.g., endogenous, environmental, or experimental variation) and decide which sources of variation are important to control for and include in their designs. Endogenous variation refers to the genetic and/or phenotypic variation in model organisms. This type of variation can be minimized or leveraged by controlling the genetic background of the organisms or changing the size of the sample population in the study. Environmental and experimental variation are both types of exogenous variation, variation that is external to the study organism(s). Environmental variation includes the environmental conditions (e.g., temperature, humidity, food type) that may impact the organisms in the study. The impact of environmental variation is often regulated by making environmental conditions as similar as possible between different samples. Experimental variation, also referred to as measurement error, can be minimized by increasing the number of technical replicates and averaging the measurement values or by choosing more precise instruments if available. Recognizing, anticipating, and accounting for variation requires a conceptual understanding of variation in biology and is essential to producing experimental results that are generalizable yet precise (Altman and Krzywinski, 2015).
Variation is also integral to the representations and statistical analyses used to make sense of data. Researchers may use mathematical representations, such as mean or SD, or graphical representations to describe the data and the variation present in the data (Krzywinski and Altman, 2013, 2014). Information obtained from the graphical and mathematical representations, as well as a researcher’s knowledge about sources of variation, helps to guide the choice of statistical tests and inform the interpretation of those tests (Krzywinski and Altman, 2013; Altman and Krzywinski, 2015). This quantitative understanding of variation is necessary for researchers to draw accurate conclusions about their data.
Students’ Difficulties with Understanding Variation
Variation has been described as a concept that is integral to a student’s ability to reason, make sense of, and master topics in both statistics and biology (Batzli et al., 2016; Patel and Pfannkuch, 2018). Much of the work that has been done exploring students’ difficulties with biological variation has focused on their struggles in understanding the role of endogenous variation in genetics and evolution (e.g., Nehm and Ridgway, 2011; Dauer et al., 2013; Bray Speth et al., 2014; Zhao and Schuchardt, 2019). These studies have shown that students fail to understand how variation arises as the result of changes to DNA during copying and how those changes lead to variation within a population forming the basis for evolution (Nehm and Ridgway, 2011; Dauer et al., 2013; Bray Speth et al., 2014; Zhao and Schuchardt, 2019). More fundamentally, most children and most adults deny the existence of within-species variation, and both groups are less likely to identify traits internal to the organism (e.g., organ shape) as variable (Shtulman and Schulz, 2008). These difficulties with identifying endogenous variation may partly explain why students have trouble recognizing sources of variation beyond experimental error and accounting for that variation in experimental design (Kuhn and Dean, 2004; Dasgupta et al., 2014). The tendency to focus on experimental error can cause students to make incorrect assumptions when interpreting their data (Dasgupta et al., 2014). For example, a lack of fit between predictions and results is attributed to errors in measuring or data collection (Dasgupta et al., 2014). Instead of evaluating whether the ideas about the phenomenon that led to a prediction are incorrect, students look for ways to reduce experimental error (e.g., being more careful, using a better instrument).
The issues that students have with experimental design and interpretation resulting from conceptual difficulties in understanding sources of variation are further exacerbated by the challenge of evaluating and comparing variation quantitatively in statistical applications. Students’ difficulties with understanding quantitative expressions of variation and how they connect to features of variation in scientific phenomena have been well documented (delMas et al., 2007; Garfield and Ben-Zvi, 2007). Students may be able to compute measures of variation (e.g., SD), but they are not able to make connections between the research components and the components of the mathematical expression (e.g., distance of each measurement from the mean and sample size; Garfield and Ben-Zvi, 2007). Thus, even though students might be shown how to calculate a t-statistic using differences between means and average SD, the conceptual idea that the differences between means are being compared with the average variation in the samples is lost. This may explain why students have difficulty factoring in the effect of sample size and variation in the population when interpreting significance tests, leading to incorrect conclusions about their data (Castro Sotos et al., 2007; Hicks et al., 2021). If students do not factor in sample size when making interpretations of statistical results, they may also be unlikely to consider sample size when designing their experiments (e.g., Dasgupta et al., 2014).
Part of the reason that students may have difficulty with using statistics and understanding variation in experimental design and analysis is that statistics is often taught separately from biology laboratory courses (Metz, 2008; Remsburg et al., 2014; Olimpo et al., 2018). Thus, the biological and statistical ideas about variation are separated by course structure. A few curricular interventions have been developed that are situated in biology laboratory and lecture courses (Metz, 2008; Colon-Berlilngeri and Burrowes, 2011; Remsburg et al., 2014; Marsan et al., 2016; Olimpo et al., 2018). These curricula tend to focus on building specific siloed skills in experimental design, interpretation of statistical representations, and/or statistical analysis of data. With this approach, quantitative reasoning is separated from conceptual understanding of variation, which can cause students to have difficulty transferring their knowledge to more complex or novel situations (Schuchardt and Schunn, 2016; Eichenlaub and Redish, 2018). When discussions and representations of variation are situated in real-world biological data as part of a model-based approach, students demonstrate better understanding of the sources of variation and develop better representations of variation (Lehrer and Schauble, 2004). Therefore, the BioVEDA curriculum uses a model-based approach (Svoboda and Passmore, 2013) across five short (25- to 40-minute) modules to integrate the exploration of sources of variation in biological investigations with the development of mathematical representations used in statistical analyses. These modules have been designed to be highly adaptable to multiple laboratory curriculum contexts.
Model-Based Curricular Approaches
“Models” and “modeling” are terms that are used in both science and statistics. Statistical models are defined as descriptive representations of how variables within a system relate to one another mathematically (Pfannkuch et al., 2016). Statistical models need to include a mathematical or computational representation that allows for a statistical test of how well the model represents the real-world system (Pfannkuch et al., 2016). In contrast, in science, a conceptual model is defined as a set of ideas about a scientific phenomenon that can be used to provide explanations and make predictions (Svoboda and Passmore, 2013). Scientific conceptual models may include mathematical representations of the relationships between variables, but they are not required, and scientific conceptual models often also include other representations of the mechanisms or processes that connect the objects within the system (Dauer et al., 2013).
Both scientific conceptual models and statistical models are built through an iterative modeling cycle (Halloun, 2007; Pfannkuch et al., 2016). In both cases, participants engage in the modeling cycle to develop better understanding of a real-world phenomena (Svoboda and Passmore, 2013; Pfannkuch et al., 2016). Scientists iteratively construct representations and develop theories about a phenomenon as they collect or are provided with data about the phenomenon (Halloun, 2007; Svoboda and Passmore, 2013). In scientific modeling, during the observation phase of the cycle, scientists gather data about a real-world phenomenon and decide which entities, processes, or relationships to include in the model. During the generation phase, scientists form ideas about the phenomenon that are represented in multiple ways. Representations for the same phenomenon should have features in common, but no one representation will provide a complete description or explanation of the phenomenon (Hestenes, 2010). Taken together, the representations constitute the scientist’s mental model, the description and explanation of the patterns and mechanisms in the scientific phenomenon. In the verification phase, the scientist checks the model against observations and data produced through experiments. In the evaluation phase, the scientist revises or accepts the original model based on the new findings (Halloun, 2007; Passmore et al., 2009). During this phase, the new and original models are compared or the scientist’s model is compared with other models to decide which model best fits the known data about the phenomenon.
Some curricula that have been described as model based only ask students to engage with specific phases of the scientific modeling cycle. For example, one curriculum situated in biology has students examine representations (e.g., picture of DNA, graph of data, picture of life cycle) to develop the idea that scientific models are simplified representations of ideas or processes that are composed of objects and relationships between objects (Dauer et al., 2013). Students draw concept map–type pictures that represent the relationships between objects as part of their study of the genetic basis of evolution (Dauer et al., 2013). These concept maps are revised over time in response to peer feedback and additional instruction and are referred to as students’ models of the genetic basis of evolution. Students are thus engaging in the representation and evaluation phases of the modeling cycle, but do not participate in model generation or verification. In another curriculum, students compare existing scientific models to determine which model best fits a set of data and then reject, accept, or make revisions to the model (Stewart et al., 2005). In this curriculum, students are participating only in the evaluation phase of the modeling cycle, determining which of two competing models to accept and whether the model needs revisions. Neither curriculum as described has students engage in the process of using data analysis to build conceptual models and then test and revise the initial model as necessary. However, there are model-based curricula in biology that do have students participate in the full modeling cycle (Schuchardt and Schunn, 2016; Malone et al., 2017; Hester et al., 2018). One of these was designed for use in undergraduate biology laboratory classes with the goal of having students develop an understanding of mechanisms underlying biological phenomena (Hester et al., 2018).
The statistical modeling cycle shares features with the scientific modeling cycle. Statistical modeling involves data modeling (generating a statistical model that fits the data; e.g., line of best fit), data generation, assessment of fit, revision of model if needed, and finally, application to real-world phenomena (Pfannkuch et al., 2016). The key difference is that scientific modeling seeks to generate and evaluate a conceptual model that explains the mechanisms of scientific phenomena, while statistical modeling seeks to generate and evaluate a statistical model that describes the relationships between variables. Curricula are starting to be developed that ask students to engage in statistical modeling as well (Pfannkuch et al., 2018). As with biology, different curricula focus on different aspects of the statistical modeling cycle (reviewed in Pfannkuch et al., 2018). Many of these curricula have been developed to teach statistics in mathematics courses at the middle and high school levels.
Use of the full modeling cycle in a model-based curriculum is supported by theory about the pedagogical advantages of invention (Schwartz and Martin, 2004) and multiple representations (Ainsworth, 2008). Based on theoretical work on transfer, iterative inventions of multiple representations around a central concept should support students in transferring their understanding to new contexts (Nokes-Malach and Mestre, 2013). If one of these representations includes mathematical equations, then such an approach should allow students to connect conceptual and mathematical concepts, aiding in mathematical sense-making and thus problem solving (Eichenlaub and Redish, 2018). This approach has been successful at the high school level in both biology and physics curricula, resulting in students displaying increased conceptual understanding (Wells et al., 1995; Schuchardt and Schunn, 2016; Malone et al., 2017) and being better able to transfer their knowledge to novel problems and flexibly switch between conceptual and quantitative problem-solving approaches (Malone, 2008; Schuchardt, 2016; Schuchardt and Schunn, 2016).
Therefore, model-based instruction that focuses on variation has the potential to build understanding of variation from both statistical and biological perspectives. Model-based instruction has been used with upper elementary and lower middle school students to develop multiple representations of variation of a biological phenomenon (Lehrer and Schauble, 2004). These students are able to progress from pictorial to graphical to mathematical representations of variation, increasing both their understanding of endogenous and/or exogenous variation within a sample and their ability to describe how their representations depict this variation (Lehrer and Schauble, 2004). Perhaps because of their age, they were not asked to relate their representations to canonical mathematical expressions of variation or apply them to problem solving. Moreover, they did not integrate their models of variation with experimental design and analysis. Model-based approaches to instruction of statistics in college biology laboratory courses have not been implemented and assessed.
Study Objectives
The BioVEDA curriculum is designed to allow undergraduate students in a biology laboratory context to develop a model of the connections between the sources of variation in biological investigations and quantitative expressions of variation throughout experimental design and analysis (described in detail in Dewey et al., 2020). The modeling that students engage in shares attributes with both statistical and scientific modeling. Like scientific modeling, the model that students build is a conceptual model, a set of ideas about variation in the context of experimental design and analysis. These ideas include identification of sources of variation, how measurement strategies impact variation, how variation can be represented mathematically and graphically, and how statistical tests factor in variation when comparing two samples. Like statistical models, the model students are building is descriptive (not mechanistic), but it can be used to make predictions about the impacts of experimental design strategies and the results of analyses. Students engage in specific aspects of the modeling cycle, including building representations and conceptual models of variation from data, making predictions based on these models, and refining their representations and models by analyzing additional data (Figure 1). A more detailed description of the curriculum is provided below.
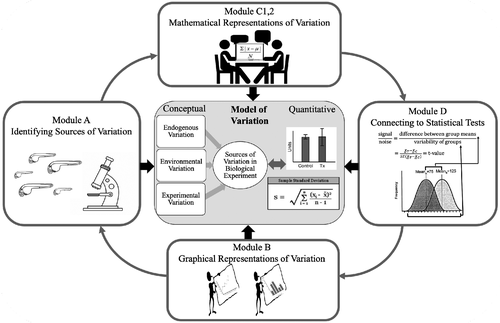
FIGURE 1. BioVEDA curriculum: Developing a model of variation in experimental design and analysis.
The current study explores the effect of the BioVEDA curricular intervention using a quasi-experimental design. This study will first address whether the model-based curricular intervention affects students’ understanding of biological variation in experimental design and analysis. Then, because previous research has shown that different factors such as gender (Metz, 2008; Maloney et al., 2013) and prior knowledge (Kalyuga, 2007; Metz, 2008) can impact learning and performance on assessments, this study will explore how students’ gender, prior statistics exposure, and incoming knowledge (as measured by pretest score) affect the impact of the curricular intervention. Finally, this study will investigate whether any effect of the curricular intervention persists into a later introductory biology laboratory course where students are asked to design and run their own experiments.
METHODS
Study Context
This study was conducted in the context of a required two-semester-long introductory biology laboratory course for undergraduate biology majors at a large midwestern R1 university. The first-semester course (BIOL 1961) is divided into multiple sections of approximately 20 students taught primarily by graduate student teaching assistants (GTAs). On average, there were 16 sections for each of the semesters of data collection in this study. Students in this course meet twice a week for 3 hours. During the first 6 weeks of the course, termed “Bootcamp,” students are taught basic laboratory skills and introduced to different project areas within which they can choose to run a project during the second-semester course (BIOL 3004), which is designed as a course-based undergraduate research experience (Auchincloss et al., 2014). At the end of Bootcamp, students pick which project area they would like to work on and begin “Project-Specific Training,” which lasts through the rest of the first-semester course (Figure 2). Students generally enroll in these lab courses during freshman or sophomore year. The student pool enrolled in these courses is 65% female, 20% domestic students of color, and ∼20% first-generation college students. The curricular intervention of this study was implemented during the first 6 weeks of BIOL 1961 (Figure 2). While students learned about and used statistics to analyze their own data in BIOL 3004, no curricular intervention was done in this course. The rest of the methods will focus on BIOL 1961. This study is approved under the University of Minnesota Institutional Review Board no. STUDY00003137.
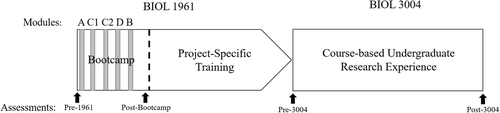
FIGURE 2. Placement of tasks and assessments throughout the two-semester course sequence.
Research Design
Using an iterative design-based approach, five short curricular modules were developed that ask students to build a model of biological variation and apply this model to experimental design and analysis. A quasi-experimental design was used to implement this curricular intervention. Half of the sections had instruction as usual in laboratory exercises designed by the course coordinators (referred to as the “Traditional” curriculum). For the other half of the sections, instruction in the Traditional curriculum was supplemented by the five intervention modules (referred to as the “Intervention” curriculum). All GTAs participated in weekly course-preparation meetings facilitated by the course coordinators that supported the procedural implementation of the Traditional curriculum. Traditional GTAs also received 4 hours of professional development on student-centered pedagogy, while GTAs implementing the Intervention curriculum received four hours of curriculum-specific professional development (Hicks et al., Unpublished data).
Curriculum Description
Traditional Curriculum.
The Traditional curriculum taught during Bootcamp is based on a lab manual containing detailed procedures for laboratory exercises that students complete in class in a largely scripted manner. The Traditional curriculum content includes laboratory techniques, experimental design, and data analysis. All students received instruction in the Traditional curriculum. Topics related to statistics such as measurement, graphing of data, t-tests, the meaning of the p value, and the effect of sample size were covered in the Traditional curriculum and taught via direct instruction that focused on procedures.
Intervention Curriculum.
The Intervention curriculum consisted of five short (25- to 40-minute) modules that served as replacements for or supplements to Traditional curriculum activities during Bootcamp. The topics covered by these modules were also taught in the Traditional curriculum as described earlier, however the Intervention modules were taught via a student-centered model-based approach with all topics connected to the concept of variation. These modules have students build conceptual and quantitative components of a model for biological variation that is situated in and applied to experimental design and analysis (Figure 1). A complete description of these modules has been published elsewhere (Dewey et al., 2020), but brief descriptions of the activities are presented in the following sections, and examples of task instructions and samples of student work are provided in Supplemental Table S1. The first three modules (A, B, and C1) focus on building an understanding of sources of variation in biological experiments and connecting that understanding to mathematical and graphical representations. The last two modules (C2 and D) have students examine the effect of sample size on variation and then use their model of variation to make connections to the calculation and interpretation of statistical tests (specifically the t-test). While the activities within the modules are designed as a coherent whole, the data and investigation context used in these modules, as well as the order of the modules, can change, making the curriculum highly adaptable. The modules are lettered to reflect the conceptual order in which they were developed (i.e., Modules A, B, C1, C2, and D). However, because the order of implementation is designed to be somewhat flexible, the modules are described in the order in which they were implemented in this laboratory course to align with the Traditional Curriculum.
Module A: Identifying Sources of Variation.
Module A asks students to identify different sources of variation within a biological experiment (i.e., endogenous, experimental, or environmental variation) and then outline different measurement strategies that would deal with the different sources of variation. Students discuss and use two different measurement strategies to generate data. Once their data are collected, they discuss the impact of these measurement strategies on the data and which strategy might be more appropriate given different relative weightings of sources of variation. This activity helps students build their conceptual understanding of variation (Figure 1).
Module C1: Generating Mathematical Representations of Data.
Module C1 asks students to develop mathematical expressions that capture variation in data. Students generate two mathematical expressions that represent the central tendency and spread of the data collected in module A. Students discuss the relationship between data spread and sources of variation in their experiment. This module lays the foundation for making connections between statistical tests and the presence of variation in the data to inform data analysis, building up the quantitative components of students’ model of variation (Figure 1).
Module C2: Applying Mathematical Representations of Data.
Module C2 asks students to explore the impact of sample size on the mathematical representations of data they developed in module C1. Student first discuss their ideas about the relationship between sample size, mean, and SD. Then students use data to check their understanding of these relationships. This activity primes student to think about the role of sample size in experimental design and how it interacts with variation, helping students make connections between the conceptual and quantitative components of their model of variation (Figure 1).
Module D: Statistical Analysis of Data.
Module D asks students to apply the model of variation they have generated to a statistical test (specifically a t-test) to understand why variation makes statistical tests necessary and how central tendency and spread of data comparisons are represented in the mathematical formula. Students identify components of the t-statistic based on the mathematical expressions they developed in module C1. Students then run a t-test and use graphical representations to discuss how to interpret the results based on the amount of variation present in the sample. This activity helps students connect multiple ideas about variation and its role in the interpretation of experimental results (Figure 1).
Module B: Generating Graphical Representations of Data.
Module B asks students to connect the mathematical expressions of variation they developed to graphical representations of variation. This helps students form a more complete representation of the model of variation (Figure 1). Students use data to generate graphical representations, specifically aiming to visualize the mean and the variation in the data of both control and experimental conditions. Students then discuss which graphs best represent the quantitative information generated from applying mathematical expressions of central tendency and data spread.
Data Collection.
The BioVEDA assessment was used to evaluate the effectiveness of the intervention curriculum (Hicks et al., 2020). The BioVEDA assessment has questions that specifically target students’ understanding of biological variation, how that variation is represented in statistical equations, and the application of the conceptual and quantitative knowledge of variation to experimental design and analysis. No other published assessment on statistics (e.g., Comprehensive Assessment of Outcomes in Statistics; delMas et al., 2007), biostatistics (e.g., Statistical Reasoning in Biology Concept Inventory; Deane et al., 2016), or experimental design (e.g., Biological Experimental Design Concept Inventory; Deane et al., 2017) adequately covers these topic areas. The BioVEDA assessment has been shown to measure a single construct (variation in experimental design and analysis; Hicks et al., 2020). Rasch analysis has demonstrated that the items have a range of difficulty that can capture the ability range of this population (Hicks et al., 2020) Moreover, this instrument is able to distinguish between groups of students who should have different ability levels (undergraduate students who have not yet taken a college biology laboratory course, undergraduate students who have completed 1 year of a college biology laboratory course, and graduate students; Hicks et al., 2020). Sample items from the published instrument are included in Supplemental Table S2.
Assessment data were collected from students enrolled in either BIOL 1961 or BIOL 3004. All students were asked to take the assessment electronically via Qualtrics at four different time points: on the first day of BIOL 1961, at the end of Bootcamp (6 weeks into the semester), at the beginning of BIOL 3004, and at the end of BIOL 3004 (Figure 2). When taking the assessment, students were given the opportunity to opt out of having their data used in the study. Approximately 10% of students or fewer opted out each semester. Students were also asked about their previous experiences with statistics and to self-identify gender on the assessment.
Data were collected over the course of four semesters (Fall 2018–Spring 2020). Analysis of the impact of the curriculum on students enrolled in BIOL 1961 included data from the Fall 2018, Fall 2019, and Spring 2020 semesters. School closing due to a weather event disrupted instruction for BIOL 1961 students in Spring 2019. Bootcamp was concluded before the switch to online instruction in Spring 2020. Analysis of the long-term impact of the intervention included data from students enrolled in BIOL 1961 in Fall 2018 and Fall 2019 who took BIOL 3004 in Spring 2019 and Spring 2020, respectively. Students were incentivized to complete the assessment through the awarding of course points that made up less than 0.5% of the course grade. Students who opted out of the study could still earn points for completing the assessment. To ensure that students were not simply guessing on the assessments, a “gotcha” question was included that told students which answer to choose. Any student who answered the gotcha question incorrectly was excluded from the study (fewer than 10% of students answered the gotcha question incorrectly). In addition to the use of the gotcha question to identify guessing, the pre-1961 and post-Bootcamp scores were examined for any extreme differences that would indicate that a student was likely guessing on the post-Bootcamp assessment but answered the gotcha question correctly by chance. An extreme difference was defined as a having a pre-1961 score of 75% or higher (answered at least 12 questions correctly) but a post-Bootcamp score of 31.25% or lower (answered five or fewer questions correctly). Two students were found to have an extreme difference between their pre-1961 and post-Bootcamp assessment scores and were excluded. In total, 527 students took both the pre-1961 and post-Bootcamp assessments (146 from Fall 2018, 133 from Fall 2019, 248 from Spring 2020). There were 127 students who took the assessment at all four time points (57 from the Fall 2018 Cohort and 70 from the Fall 2019 Cohort).
Data Analysis.
Normalized gain scores, [(Postscore% − Prescore%)*100/(100 − Prescore%)], were calculated to assess students’ change in understanding between pre-1961 and post-Bootcamp (Hake, 1998). Normalized gain scores were used as opposed to regular gain scores to account for differences in how much each student was able to gain based on the pre scores. Given that the data collected for this study are nested (i.e., students are nested within a specific TA), an unconditional hierarchical linear model was run to determine where there was between-TA variation in students’ normalized gain scores that needed to be explained using a multilevel model. The chi-square test for the variance of random effects was not significant, τ00 = 11.389, χ2(40) = 47.684, p = 0.19. The intraclass correlation coefficient of the model was 0.007, meaning that TA differences only accounted for 0.7% of the variation in students’ normalized gain scores. These results indicate that there is not enough variation between TAs to warrant the use of a hierarchical analysis (Raudenbush and Bryk, 2002). The additional analyses used to address the three research questions of this study are described in the next section.
Effect of the Intervention on Students’ Understanding.
A two-sample t-test was used to compare the normalized gain scores of students in the Traditional and Intervention curriculum groups. Two-sample t-tests were also used to compare the pre scores of students in the Traditional and Intervention curriculum groups and determine whether the average normalized gain of each curriculum group was significantly different from zero. The normalized gain scores and pre-1961 scores met the assumptions for a t-test (i.e., normality, homogeneity of variance). Cohen’s d was used to assess the effect sizes for all t-test analyses. A value of 0.2 indicates a small effect, a value of 0.5 indicates a medium effect, and a value of 0.8 indicates a large effect (Cohen, 1998).
Impact of Gender, Prior Statistics Exposure, and Pretest Score on the Effect of the Intervention.
Students were asked to self-identify gender, and five students who identified as nonbinary were excluded from the gender analysis. A two-sample t-test was used to compare the pre-1961 scores of men and women. An analysis of variance (ANOVA) was used to assess the possible interaction between curriculum condition and student gender on normalized gain scores. These data met all the assumptions for the t-test and ANOVA. Cohen’s d was used to assess the effect size for the t-test analyses. The effect size for the ANOVA was determined using the generalized eta-squared (η2G). A value of 0.01 indicates a small effect, a value of 0.06 indicates a medium effect, and a value of 0.14 indicates a large effect (Vacha-Haase and Thompson, 2004).
When split by whether a student had previously taken a statistics course, students’ pre-1961 scores did not meet the assumption of homogeneity of variance. Therefore, a Welch’s t-test was used to assess whether students’ pre-1961 scores differed based on whether a student had previously taken a statistics course. Students’ normalized gain scores met the assumptions for an ANOVA, so an ANOVA was used to assess the possible interaction between curriculum condition and whether a student had previously taken a statistics course on the normalized gain scores. Cohen’s d for Welch’s t-test was used to assess the effect size for the t-test analysis. This Cohen’s d uses the average variance rather than the pooled variance of the samples and is evaluated using the same cutoffs as the regular Cohen’s d (Cohen, 1998). The effect size for the ANOVA was determined using η2G.
To explore a potential interaction between curriculum condition and students’ pretest scores on normalized gain scores, students’ pre-1961 scores were split into three groups using the tertiles (i.e., thirds) of the distribution of scores. Students with scores in the bottom third of the pre-1961 scores (scored less than 43.75%) were designated as the “Low” pretest group. Students with scores in the middle third of the pre-1961 scores (scored between 43.75% and 56.25%) were designated as the “Medium” pretest group. Students with scores in the top third of the pre-1961 scores (scored above 56.25%) were designated as the “High” pretest group. When split by pretest score group, students’ normalized gain scores did not meet the assumption of homogeneity of variance. Therefore, a Kruskal-Wallis analysis was performed on the pretest group variable and the curriculum group variable for each pretest group. Dunn’s post hoc test was used to explore significant differences within each of these variables, and p values were adjusted using the Bonferroni multiple testing correction method. The effect size for the Kruskal-Wallis analysis was determined using eta-squared based on the H statistic (η2H). A value of 0.01 indicates a small effect, a value of 0.06 indicates a medium effect, and a value of 0.14 indicates a large effect (Vacha-Haase and Thompson, 2004). The effect sizes for the Dunn’s post hoc test comparisons were determined using Cohen’s d for a Welch’s t-test to account for the heterogeneity of the variances in these data.
Persistence of the Intervention Curriculum Effect.
A two-way repeated-measures ANOVA was performed to explore the effect of the Intervention curriculum over time (i.e., into and through BIOL 3004) on students’ percent scores on the assessment. The effect size for the repeated-measures ANOVA was determined using η2G. Post hoc pairwise t-test comparisons were performed to further investigate differences found through the two-way repeated-measures ANOVA, and p values were adjusted using the Bonferroni multiple testing correction method. The effect size of these post hoc pairwise t-tests was determined using Cohen’s d. The assumption of normality was met for the two-way repeated-measures ANOVA. The assumption of sphericity was evaluated while running the two-way repeated-measures analysis. The analysis was corrected using the Greenhouse-Geisser epsilon for any variable that violated the assumption of sphericity.
An alpha level of 0.05 was used to determine statistical significance for all analyses. All analyses were performed in R v. 4.0.1 (R Core Team, 2020) using the packages hlmer (Dahlke, 2020) and rstatix (Kassambara, 2020).
RESULTS
Students in the Intervention Curriculum Show an Increase in Normalized Gains
Students in the Traditional curriculum group showed an average normalized gain of −0.56% (Mpre = 49.8%, Mpost = 52.3%), which was not statistically different from zero, t(252) = −0.21, p = 0.83, Cohen’s d = 0.01. Students in the Intervention curriculum group showed much larger normalized gains (MNgain = 7.6%; Mpre = 50.5%, Mpost = 55.7%) that were statistically different from zero, t(273) = 3.38, p < 0.001, Cohen’s d = 0.2. The difference between these two groups was statistically significant, t(525) = 2.37, p = 0.02, with a small effect size (Cohen’s d = 0.21; Figure 3). There was no significant difference in the pre-1961 scores between the two groups of students, MTrad = 49.8%, MInt = 50.5%, t(525) = 0.54, p = 0.59, Cohen’s d = 0.05. Pre and post scores by topic area (Hicks et al., 2020) are reported in Table 1. The pre to post difference for Traditional students ranged from −2 for interpreting p values to +5 for representing observed variation in a data set. The pre to post difference for Intervention students ranged from +1 for interpreting p values to +10 for understanding how observed variation impacts the outcome of statistical tests.
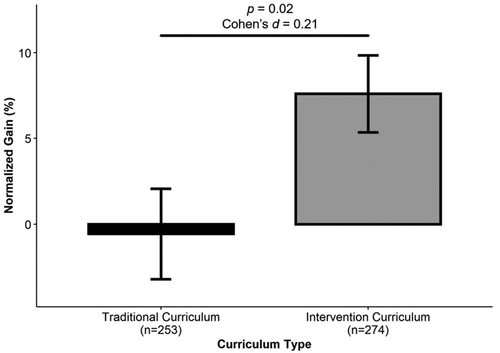
FIGURE 3. The Intervention curriculum improves students’ understanding of variation in biological investigations. Average normalized gain scores are compared between students in the Traditional curriculum group and students in the Intervention curriculum group. Significance determined using a two-tailed t-test. Bar ± error bar = mean ± SEM. Normalized gain scores ranged from −200% to 100%.
| Investigative phase | Topic | Assessment questions | Traditional | Intervention | ||
|---|---|---|---|---|---|---|
| Pre-1961 score (SEM) | Post-Bootcamp score (SEM) | Pre-1961 score (SEM) | Post-Bootcamp score (SEM) | |||
| Experimental design | Identifying sources of variation in an experiment | 1, 7 | 58 (2.1) | 61 (2.3) | 57 (2.1) | 64 (2) |
| Controlling for different sources of variation in an experiment | 2, 3, 4, 6 | 66 (1.6) | 70 (1.7) | 69 (1.6) | 72 (1.6) | |
| Understanding the relationship between sample size and genetic variation in a biological data set | 5 | 78 (2.6) | 77 (2.6) | 76 (2.6) | 79 (2.5) | |
| Data analysis | Representing observed variation in a data set | 13, 14 | 46 (2.2) | 51 (2.2) | 44 (2) | 53 (2.2) |
| Understanding how observed variation impacts the outcome of statistical tests | 8, 9, 10, 11 | 36 (1.6) | 40 (1.7) | 37 (1.6) | 47 (1.6) | |
| Interpreting p values generated by statistical tests | 12, 14, 15, 16 | 41 (1.6) | 39 (1.5) | 42 (1.6) | 43 (1.5) | |
Normalized Gains Are Not Affected by Gender or Prior Statistics Exposure
Potential interactions were explored between curriculum condition and student gender and prior statistics exposure.
Men (n = 192) scored slightly higher than women (n = 330) on the pre-1961 assessment, MMen = 51.9%, MWomen = 49.1%; t(520) = −1.98, p = 0.048, Cohen’s d = 0.18. However, there was no significant interaction between gender and curriculum condition on students’ normalized gain scores, F(1, 518) = 0.006, p = 0.94, η2G < 0.001. There was also no main effect of gender on students’ normalized gain scores, F(1, 518) = 0.631, p = 0.43, η2G = 0.001, suggesting that men and women benefited equally from the Intervention curriculum.
Students were also asked about their prior statistics exposure on the assessment. Approximately 40% of students had taken a statistics course previously, either in high school or college. There was no significant difference in the pre-1961 scores between students who had taken a statistics course and those who had not, MNoStats = 51%, MStats = 49%; t(496.2) = 1.25, p = 0.21, Cohen’s d = 0.11. Additionally, there was no significant interaction between prior statistics exposure and curriculum condition on students’ normalized gain scores, F(1, 523) = 0.002, p = 0.96, η2G < 0.001. There was also no main effect of prior statistics exposure on students’ normalized gain scores, F(1, 523) = 0.1, p = 0.76, η2G < 0.001. Students benefited equally from the Intervention curriculum regardless of whether they had prior exposure to statistics.
Students’ Pretest Scores Impact Their Normalized Gains
Given previous work showing the importance of pre knowledge on test performance (Kalyuga, 2007), the possibility of an interaction between students’ pre-1961 scores and their curriculum condition on normalized gain scores was tested. There were statistically significant differences in the normalized gains among the pretest groups with a small to medium effect size, Kruskal-Wallis test, H(2) = 26.54, p < 0.001, η2H = 0.05. For both the Traditional and Intervention curricula, students in the Low pretest group, NTrad = 74, NInt = 66, showed greater normalized gains than students in the High pretest group, NTrad = 67, NInt = 82; Dunn’s post hoc test, Traditional: MLow = 15%, MHigh = −20.7%, z = −3.07, p.adjust = 0.006, Cohen’s d = 0.75; Intervention: MLow = 18.8%, MHigh = −2.6%, z = −4.37, p.adjust < 0.001, Cohen’s d = 0.55 (Figure 4). There was no significant difference in normalized gains between the Traditional and Intervention students in the Low pretest group, MTradLow = 15%, MIntLow = 18.8%, H(1) = 1.03, p = 0.31, η2H < 0.001. There were marginally significant differences with small effect sizes between the normalized gains of Traditional and Intervention students in the Medium pretest group, NTrad = 112, NInt = 126, MTradMed = 1.2%, MIntMed = 8.4%, H(1) = 3.07, p = 0.08, η2H = 0.01, and the High pretest group, MTradHigh = −20.7%, MIntHigh = −2.6%, H(1) = 3.19, p = 0.07, η2H = 0.02. Intervention students made slightly higher gains than Traditional students in the Medium pretest group and lost less of their knowledge than the Traditional students in the High pretest groups (Figure 4).
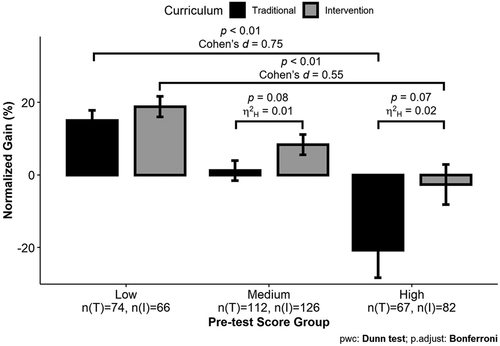
FIGURE 4. Incoming pretest score and curriculum condition impact students’ normalized gain scores. Kruskal-Wallis tests were used to compare normalized gain scores across the two curriculum groups within three different pretest score categories. Effect sizes were determined using generalized eta-squared based on the H-statistic (η2H). There was no significant difference found between the curriculum conditions in the Low pretest score group. Differences between curriculum conditions in the Medium and High pretest score groups were marginally significant, with small effect sizes, and were therefore included on the graph. Dunn’s post hoc test with a Bonferroni correction was used to compare normalized gains between the Low and High pretest score groups within each curriculum condition. Effect sizes were determined using Cohen’s d. Bar ± error bar = mean ± SEM.
The Intervention Curriculum Produces Sustained Learning Gains over Time
The Intervention curriculum was implemented in the first 6 weeks of the first-semester course. The persistence of the effect of the Intervention curriculum into and through the second semester course, where TAs and course structure have changed, was investigated. Matched data from 127 students who took the assessment at all four time points were used for this analysis. The pre-1961 scores of the 127 students who took the assessment at all four time points were significantly higher than the pre-1961 scores of the 400 students who did not take the assessment at all four time points, Mprepost = 49.3%, Mallfour = 52.9%, t(525) = −2.18, p = 0.03, Cohen’s d = 0.22. However, there was no significant difference between the pre-1961 scores for the Traditional (N = 56) and Intervention (N = 71) students who took the assessment at all four time points, MTrad = 51.5%, MInt = 54%, t(125) = 0.89, p = 0.37, Cohen’s d = 0.16. For Intervention students, the post-Bootcamp scores for students who took the assessment at all four time points were significantly higher than for students who did not, Mprepost = 53.1%, Mallfour = 63.2%, t(272) = −4.2, p < 0.001, Cohen’s d = 0.58. For Traditional students, there was no significant difference between the post-Bootcamp scores for these groups, Mprepost = 51.8%, Mallfour = 53.9%, t(75.952) = −0.71, p = 0.48, Cohen’s d = 0.12.
There was no significant interaction between curriculum condition and time point, F(3, 375) = 2.015, p = 0.11, η2G = 0.005. However, this analysis did show a small effect of curriculum condition wherein students in the Intervention group had higher scores on average than the Traditional students, F(1, 125) = 6.675, p = 0.011, η2G = 0.035, and a small effect of time where students’ scores increased over time, F(3, 375) = 12.856, p[GG] < 0.001, η2G = 0.033. Intervention students’ percent scores on the assessment were significantly higher at all three post-intervention time points (post hoc pairwise t-tests; Figure 5).
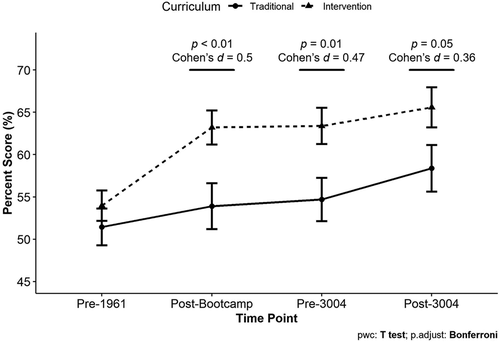
FIGURE 5. The effect of the Intervention curriculum persists into and through BIOL 3004. This analysis only includes students who had scores at all four time points. Matched percent scores are compared between students in the Traditional curriculum group (n = 56) and students in the Intervention curriculum group (n = 71). Significance determined using post hoc pairwise t-tests with a Bonferroni correction. Points ± error bars = mean ± SEM. Percent scores ranged from 6.25% to 100%.
DISCUSSION
This study assessed the effectiveness of a model-based curricular intervention aimed at improving students’ understanding of biological variation in experimental design and data analysis. Students who received the curricular intervention showed significantly higher normalized gains compared with students who did not receive this intervention. The modules of the Intervention curriculum ask students to generate representations and explanations that connect biological variation to principles of experimental design and analysis. In contrast, the Traditional curriculum uses a largely procedural and siloed approach to carrying out experimental design and data analysis. Importantly, the Intervention curriculum modules did not require a large investment of instructional time (2.5 hours over 36 hours of instruction), yet still resulted in significant, albeit small, gains in students’ understanding. One topic where Intervention students showed high gains was understanding how observed variation impacts the outcome of statistical tests. This study provides quantitative support for the efficacy of connecting statistics to concepts (Wild and Pfannkuch, 1999) and extends work using a model-based approach for statistics with middle school students to undergraduate students, complementing the qualitative observations reported in previous studies (Lehrer and Schauble, 2004). Significantly, the BioVEDA curriculum is a relatively inconspicuous, but focused intervention that can be layered over existing course curricula to yield lasting effects on student understanding of important ideas about variation in experimental biology.
The normalized gains achieved by students who received the Intervention in this study are small, representing an average gain per student of one question on a 16-question assessment. Metz (2008) reported an average normalized gain of 25% (nearly three questions on an 11-question survey) using an inquiry-based approach to teaching statistics in an introductory biology lecture and laboratory course. However, their intervention lasted for an entire semester, while our intervention was a 2.5-hour intervention implemented over the course of 6 weeks. In an intervention that was of similar length to ours, Marsan et al. (2016) reported gains of one question on two different assessments (one on experimental design and one on graphical interpretation.) For a 1-hour intervention, gains of 0.6–0.8 questions were reported on a 12-question assessment (Olimpo et al., 2018). A fourth intervention in a biology course (7–8 hours over the course of two semesters) did not produce significant learning gains (Remsburg et al., 2014). Combined, the data from these different interventions suggest that both course structure and the time spent on statistics are important for considering how to effectively integrate statistics instruction into biology laboratory courses.
The learning gains observed as a result of the BioVEDA intervention were not consistent across topics, with students in both the Intervention and Traditional groups performing poorly on interpreting p values on the pretest and not achieving learning gains on the posttest for this topic. This is a difficult topic that many postgraduates also fail to understand (Haller and Krauss, 2002; Goodman, 2008). Additionally, this topic was addressed at the end of the BioVEDA intervention, meaning students had less time to integrate this knowledge into their model through iteration. Developing additional modules to address challenging topics and extending the curriculum throughout the first-semester course is a promising future direction.
Traditional students did receive instruction in experimental design and data analysis on many of the same topics as the Intervention students. However, their instruction on these topics was siloed and focused on procedures (e.g., how to perform a statistical test). The instruction was not designed around constructing a conceptual model of variation with respect to experimental design and analysis. This may explain why Traditional students showed no significant normalized gains on the BioVEDA assessment, despite having pretest scores similar to those of the Intervention group. Others have suggested that compartmentalized and procedural instruction hinders students’ ability to apply concepts and skills to novel questions (Wild and Pfannkuch, 1999; Schuchardt and Schunn, 2016; Eichenlaub and Redish, 2018).
Although both Intervention and Traditional students showed knowledge gains over time, the differential effect of the Intervention persisted into and through the next semester laboratory course (BIOL 3004; Figure 5). Students who received the Intervention curriculum showed significantly higher scores on the assessment at the beginning and end of BIOL 3004. Interestingly, Intervention students who took the assessment at all four time points had higher post-Bootcamp scores than students who did not take all four assessments. This was not observed for Traditional students, perhaps because most students did not show gains with the Traditional curriculum. The difference in post-Bootcamp scores for the Intervention students could be a sampling artifact or could suggest a difference between students who took the assessment at all four time points and those who did not. For example, students who took the assessment at all four time points could be more motivated students and perhaps engaged with the curriculum more (Chi and Wylie, 2014). Metz (2008) noted the same difference in a longitudinal study of the effect of a statistics curriculum and discussed the challenges of capturing data from students who may be struggling with the curriculum. This highlights a complex problem in educational research of how to assess and report on the effectiveness of interventions for all students. We conclude from our data that the Intervention was effective in increasing some students’ understanding in a way that persisted into the future.
Previous work has shown that factors such as gender, prior statistics exposure, and incoming knowledge can have impacts on students’ learning (Kalyuga, 2007; Metz, 2008; Maloney et al., 2013). Women in our course scored slightly lower than men on the pre-1961 assessment but showed similar normalized gains. This is an important finding, given that previous studies have reported that women learn less and underperform on science tests when compared with men (e.g., Hake, 1998; Salehi et al., 2019). Metz (2008) also reported no effect of gender, suggesting that the specific curricular approaches being used in these studies do not explain gender difference. One explanation that is often provided for gender differences on assessments is that women experience greater stereotype threat and higher anxiety on mathematics assessments (Maloney et al., 2013; Salehi et al., 2019). In both this study and the work done by Metz (2008), the pre–post design keeps the effect of these factors on the performance of men and women consistent at both time points.
There was no significant difference in the pre-1961 scores between students who had taken a prior statistics course (M = 49%) and students who had not (M = 51%). This curricular intervention did not result in an interaction between prior statistics exposure and curriculum condition on students’ normalized gains. However, Metz (2008) did report an effect of prior statistics courses, with those who had not taken a prior statistics course gaining more. Notably, the students in that study displayed a larger difference in the pretest scores (M = 64% for those who had prior statistics exposure; M = 43% for those who did not). Moreover, that curricular intervention was more similar to a traditional stand-alone statistics course with siloed introduction of topics that might be taught in these courses. The model-based Intervention curriculum in this study provided a new way to look at statistics topics by presenting them as representations and consequences of biological variation as opposed to teaching procedures for performing calculations, which is a common approach in many statistics classes (Pfannkuch et al., 2018). Thus, the approach to statistics was novel for both students who had taken statistics and those who had not, which might explain why both groups benefited equally from the intervention.
There was a relationship between students’ pretest scores and curriculum group on students’ normalized gains in this study. Similar to Metz (2008), we found that students with lower pretest scores showed stronger gains than students with higher pretest scores. However, our data also suggest that students with the highest pretest scores (i.e., highest pre-1961 scores) were negatively impacted by the Traditional curriculum (Figure 4), showing an average normalized gain of about −20%, which corresponds to a loss of three questions on a 16-question assessment. In contrast, students with the highest pretest scores in the Intervention group had a smaller loss of knowledge (−2.6%). These data could represent an expertise reversal effect (Kalyuga, 2007), in which the information presented in the Traditional curriculum is beneficial for novice learners but conflicts with the understanding that students in the High pretest score group already have. Alternatively, these data could suggest that there are misconceptions being taught in the Traditional curriculum that conflict with what students in the High pretest score group already know. Either way, it seems that the Intervention curriculum is potentially buffering this effect. This buffering could be occurring because of the professional development provided to the Intervention GTAs but not the Traditional GTAs or it could be because the model-based approach gives students the opportunity to reconcile new information with prior knowledge. While the difference between the normalized gain scores of the Traditional and Intervention students with high pretest scores was only marginally significant, this comparison showed a small effect size (η2H = 0.02). Given the small sample size of this comparison, greater power is needed to confirm these results and to analyze differences by topic area to identify which areas are impacted differentially by the two curricula.
Limitations
The curricular intervention in this study was short and confined to a short period of time within the first-semester course, resulting in only small, albeit significant, gains from the pre- to post-assessment. Opportunities to apply and refine the final model of variation that students had constructed were not provided throughout the course, and these opportunities have been shown to be an important part of the model development cycle (Halloun, 2007). Further research needs to be done to incorporate such opportunities and see whether further gains are achieved. As noted earlier, not all students took both the pre-1961 and post-Bootcamp assessments, and the number who took all four assessments was even smaller. Therefore, our conclusions only apply to the group of students who took the assessments and agreed to be part of the study. Additionally, the curriculum was implemented in only one laboratory context. Biology majors at this university have high Math ACT scores and approximately 40% of students had taken a prior statistics course. Expanding curriculum implementation and evaluation to other contexts will reveal whether this curriculum will have the same effect with students who have less mathematical preparation.
CONCLUSION
This study investigated a novel approach to teaching statistics to undergraduate students in biology in which students were asked to construct a conceptual model of variation that connects representations and concepts of variation to experimental design and analysis. Within the same biology laboratory course, students who received instruction in this curriculum show greater normalized gains than students who received procedure-focused data analysis instruction. The impact of the Intervention is not affected by gender or prior statistics exposure and persists over time, at least for some students. This work provides an adaptable and expandable model for using the model-based curriculum approach in undergraduate biology laboratory contexts to improve students’ understanding of biological variation in experimental design and analysis.