Checking Equity: Why Differential Item Functioning Analysis Should Be a Routine Part of Developing Conceptual Assessments
Abstract
We provide a tutorial on differential item functioning (DIF) analysis, an analytic method useful for identifying potentially biased items in assessments. After explaining a number of methodological approaches, we test for gender bias in two scenarios that demonstrate why DIF analysis is crucial for developing assessments, particularly because simply comparing two groups’ total scores can lead to incorrect conclusions about test fairness. First, a significant difference between groups on total scores can exist even when items are not biased, as we illustrate with data collected during the validation of the Homeostasis Concept Inventory. Second, item bias can exist even when the two groups have exactly the same distribution of total scores, as we illustrate with a simulated data set. We also present a brief overview of how DIF analysis has been used in the biology education literature to illustrate the way DIF items need to be reevaluated by content experts to determine whether they should be revised or removed from the assessment. Finally, we conclude by arguing that DIF analysis should be used routinely to evaluate items in developing conceptual assessments. These steps will ensure more equitable—and therefore more valid—scores from conceptual assessments.
INTRODUCTION
Knowledge assessments that are used to measure students’ understanding of disciplinary concepts need to produce valid and reliable scores (Downing and Haladyna, 2006; American Educational Research Association, American Psychological Association, National Council on Measurement in Education [AERA, APA, NCME], 2014). This robustness is essential for high-stakes tests used, for example, in college admissions, and it is also essential for drawing inferences about student performance on low-stakes assessments, such as those within science classrooms. For example, in biology, several concept inventories have been developed that measure what students understand about specific core concepts. A variety of methods are used to explore the validity of scores during the development of assessment tools (e.g., Libarkin, 2008; Adams and Wieman, 2011; Reeves and Marbach-Ad, 2016).
During the process of validation, developers often test for differences in performance among two or more groups of students as one way of gathering evidence of the presence or absence of test bias, such as whether men and women perform differently, whether native speakers of the testing language perform consistently better than others, or whether race/ethnicity is linked with performance (Walker and Beretvas, 2001; Walker, 2011). In addition, attending to the performance of different groups is critical for equity—assessments should not discriminate against any individual (e.g., Libarkin, 2008); developers must show that performance on the assessment is not related to factors that are irrelevant to the construct being tested.
In this paper, we explain how applied data analysis techniques can be used to identify potentially biased, or unfair, test items. We define differential item functioning, or DIF, and explain the suite of statistical approaches, known as DIF analysis, used to identify DIF items—those test items for which different groups of students perform differently. After explaining the theory behind DIF analyses and describing some of the most common methods, we present two scenarios with real and simulated data to demonstrate how to conduct several types of DIF analysis. The first scenario consists of data from the Homeostasis Concept Inventory (HCI; McFarland et al., 2017), which was administered to students from a range of institutions throughout the United States. The second scenario consists of a simulated data set designed to show that the distribution of the total scores of two groups can be exactly the same, even when some test items are biased against one of those groups. Together, these cases show how DIF analyses provide a rich, nuanced understanding of how different groups perform on a test.
While some biology education articles have previously employed DIF and/or highlighted its importance (e.g., Penfield and Lee, 2010; Federer et al., 2016; Romine et al., 2016), many of the validation studies of concept inventories have not checked for DIF or potential unfairness of items. For example, none of the 22 articles in a list of biology concept inventories (SABER, n.d.) used DIF analysis to check for potential bias in their items. That said, interest in DIF analysis is growing within the biology education community. One recent paper by Deane et al. (2016) considered item bias, and others have been using and advocating for item-level analyses (Neumann et al., 2011;McFarland et al., 2017). We, along with others (AERA, APA, NCME, 2014; see also Reeves and Marbach-Ad, 2016), argue that items flagged as DIF have a strong potential to threaten the validity of scores if they are not further investigated, and therefore DIF analysis should be performed routinely when developing conceptual assessments. We conclude this paper by reviewing recent examples from biology education that used DIF analysis.
BACKGROUND
Identifying Achievement Gaps
In the high-stakes testing world, assessment researchers consistently evaluate the fairness of tests and explore the reasons behind achievement gaps (e.g., Sabatini et al., 2015; Huang et al., 2016). This type of detailed analysis occurs less frequently in the low-stakes testing world, and, if present, is typically restricted to comparing groups on test total scores (Steif and Dantzler, 2005). Differences between groups on total scores may be identified graphically with box plots, histograms, or density plots, and can also be tested empirically with t tests, chi-square tests, or regression models that account for miscellaneous fixed and random factors (Gelman and Hill, 2007; Moore et al., 2015).
In contrast to examining group differences on total scores, examining differences at the item level provides clarity as to where exactly group differences are located and whether there is any pattern in those differences. The simplest item-level analysis involves comparing the groups on the proportion of examinees who answer the item correctly (this proportion is called “difficulty” and denoted as p in psychometric classic test theory literature; Allen and Yen, 1979). However, group differences in item difficulty can be due to real and important group differences or may be blurred by the fact that one group has higher knowledge of the tested topic overall. Therefore, additional analyses are required that consider both the total score and individual item performance simultaneously.
DIF analysis encompasses a set of approaches for comparing performance of groups on individual items while simultaneously considering the students’ potential to score well on the test (Holland and Wainer, 1993; Camilli, 2006; Zumbo, 2007; Magis et al., 2010). Therefore, DIF analysis is more useful than comparing total scores for identifying potential unfairness and for assessing the causes of achievement gaps (Zieky, 2003). As we will demonstrate, DIF analysis can identify achievement gaps that are not revealed when comparing total scores (see Case Studies). To our knowledge, DIF analysis has rarely been used in the development of low-stakes tests such as concept inventories (but see McFarland et al., 2017, for an example of DIF analysis).
DIF analysis is conducted by comparing a reference group (typically the majority, or normative, group) with a focal group (typically the minority, or disadvantaged, group). For example, a study probing for bias against women would use men as the reference group and women as the focal group. Similarly, when testing whether items are biased against a historically underrepresented minority group on an assessment developed in the United States, we would consider white students as the reference group, and we might consider African-American students to be the focal group. In a similar vein, native language speakers being assessed would be considered the reference group, with language learners as the focal group.
An Item Can Measure More Than What Was Intended
DIF occurs when an item measures more than one underlying latent trait and when cognitive differences exist on one of these other, so-called secondary, latent traits (Ackerman, 1992; Shealy and Stout, 1993; Roussos and Stout, 1996). A latent trait (also known as latent knowledge, latent ability, or, more generally, latent variable) is an individual’s true knowledge or understanding of the construct being measured, and it can be estimated but not directly measured. The simplest estimate of the latent trait is total score. When developing biology concept inventories, for example, the goal is that the items only measure students’ biological concept knowledge (primary latent trait), and that additional cultural knowledge (secondary latent trait related to identity) is not necessary to answer items correctly. In other words, we wish to know whether the items only measure students’ knowledge of information relevant to the concept. The presence of DIF for a given item would indicate that the item may measure a secondary latent trait, either alone (completely missing the target concept) or in concert with the primary trait (which requires knowledge of the target concept and the secondary concept). For example, suppose a student needed both an understanding of the concept of homeostasis and knowledge of difficult English vocabulary (e.g., to understand the phrase “hypertension is characteristic of diabetic nephropathy”), that is not essential for understanding the concept of homeostasis. Moreover, if the focal group of students does not have the requisite knowledge of English, then the focal group would be more likely to answer incorrectly compared with those in the reference group even if the focal group has the same level of homeostasis knowledge as the reference group. Moreover, a test containing items exhibiting DIF could in turn create inaccurate observed total scores, resulting in inaccurate estimation of the focal group’s primary latent trait (e.g., biological concepts).
Fair or Unfair?
Although the presence of DIF is a signal that an item may be biased, it does not guarantee that the item is unfair. Rather, the presence of DIF indicates the existence of a latent trait besides the one of primary interest. Fairness is established subsequently if the secondary latent trait that was detected statistically is intentionally related to the primary latent trait. It is possible that the secondary latent trait is required by the content and the test specifications, even if the reference and focal groups perform differently.
An example of a situation in which a primary and secondary latent trait are both required for a test occurred recently in a biology admission test for medical school in the Czech Republic (Drabinová and Martinková, 2016; see also Štuka et al., 2012). On one item about childhood illnesses, DIF analysis revealed that women performed better than men. Content experts reviewed the item, and concluded that the difference occurred because women in the Czech Republic spend more time with children than men and therefore have more experience with childhood illnesses (Drabinová and Martinková, 2016). The faculty, however, still considered the item to be fair despite the gender difference, because medical experts need to be familiar with childhood illnesses. In this case, the test writers decided that the secondary latent trait, knowledge of childhood illnesses, was related to the primary concept being tested, which was biology in medicine.
Other clear examples of fair items that exhibited DIF exist in the literature (Doolittle, 1985; Hamilton, 1999; Zenisky et al., 2004; Liu and Wilson, 2009; Kendhammer et al., 2013). Even if the item flagged as DIF is later reviewed and considered fair, the act of identifying these gaps in conceptual understanding can inform teaching and, subsequently, help educators and policy makers to reduce such gaps in the future.
The Czech biology medical test shows how critical it is for content experts to review whether DIF is the result of unintended secondary latent traits (see also Ercikan et al., 2010). Only if the presence of DIF can be attributed to unintended item content (e.g., related to cultural background) or some other unintended item property (e.g., method of test administration) is the item said to be unfair. In such cases, content that is unrelated to the concept being tested increases the likelihood an individual will answer the item correctly.
Items that have been evaluated with multiple rounds of DIF analysis and content expert adjustments can help to decrease unfair achievement gaps (e.g., Penfield and Lee, 2010). For example, Siegel (2007) demonstrated ways to clarify item wording for second language learners so that they were fairly tested on the content rather than their language. In other words, ensuring that the items are clearly worded bolsters our confidence that we are truly assessing what students know. Martinello and Wolf (2012) demonstrated three situations in which individuals from focal groups responded incorrectly to math items that they were able to answer correctly during interviews. In one of the examples, a high school student from another country who was still learning English (the language of the test) did not understand words with multiple meanings the same way that native speakers would, particularly when the words used in the problem were culture bound. For example, the word “tip” can refer to tipping a waiter, but in other circumstances it means the top of an object, not a percentage of money. Thus, questions that ask students to calculate a tip for a waiter can be unfair (Martinello and Wolf, 2012). Some students will answer incorrectly even if they can demonstrate the knowledge required to do the task, in this case approximating the percentage of another number. Unfair items translate into unfair reflections of an individuals’ true ability or knowledge, and they also have the strong potential to discourage students from underrepresented groups from becoming interested in a subject (Wright et al., 2016). Thus, using DIF analysis to identify DIF items that are unfair enables us to reformulate or remove them.
METHODS FOR DETECTING DIF
In this section, we review the most commonly used statistical methods that have been developed to detect DIF (Holland and Wainer, 1993; Millsap and Everson, 1993; Camilli and Shepard, 1994; Clauser and Mazor, 1998; Magis et al., 2010). We focus on methods for tests with dichotomous items, which include binary items graded as true (1) or false (0), or as correct (1) or incorrect (0), on multiple-choice or free-recall tests. Methods for detecting DIF on other types of items (e.g., those graded on a rating, ranking, or partial-credit scale) are similar but beyond the scope of this paper. Generally speaking, statistically detecting items exhibiting DIF requires that we match students on relevant knowledge (e.g., using their total scores on the assessment being evaluated as an estimate of ability, or latent trait), and then test whether students who are matched for ability but from different groups perform similarly on a given item.
The methods for detecting DIF vary depending on how students are matched. Classical methods (e.g., Mantel-Haenszel statistic and logistic regression) match students based on their total scores; methods based on item response theory (IRT) models, such as the Wald χ2 test (also known as Lord’s test; Lord, 1980) and Raju’s area test, consider student ability as a latent variable estimated together with item parameters in the model (Hills, 1989; Millsap and Everson, 1993; Camilli and Shepard, 1994). Generally, IRT methods are computationally more demanding and require larger sample sizes. However, IRT methods are more precise than others, because they more accurately estimate the latent trait instead of using total score as the proxy.
Here, we describe the three most common approaches for detecting DIF (Table 1). First, we discuss the Mantel-Haenszel χ2 test, which functions well even for very small sample sizes (Mantel and Haenszel, 1959) and allows researchers to calculate statistics quickly using basic arithmetic. Second, we describe procedures that rely on logistic regression (Zumbo, 1999), which provides a more precise description of DIF compared with the Mantel-Haenszel procedure, and allows for distinguishing between two types of DIF: uniform and nonuniform DIF. Finally, we discuss methods based on IRT models (Lord, 1980; Raju, 1990; Thissen et al., 1994), which more accurately estimate both item characteristics and student abilities but require relatively larger sample sizes.
| Method | Strengths | Limitations |
|---|---|---|
| Classical methods | ||
| Mantel-Haenszel χ2 test | Easy to calculate by hand | Not always able to detect nonuniform DIF |
| Can handle small sample sizes | ||
| Logistic regression | ||
| Two-parameter | Able to capture nonuniform DIF | Does not account for guessing |
| Three-parameter | Accounts for guessing | Some convergence issues can be observed |
| IRT-based methods | ||
| Three-parameter logistic (3PL) IRT Wald test | More precisely estimates latent ability | Requires large sample size (N > 500 in each group) |
Mantel-Haenszel χ2 Test: Method for Small Samples
The Mantel-Haenszel test is an extension of the test χ2 for contingency tables (Agresti, 2002) that sorts students into groups based on their total scores, k (Mantel and Haenszel, 1959; Holland, 1985; Holland and Thayer, 1988). For a given item and a given level of total score k, a 2 × 2 contingency table is created (Table 2).
| Correct answer | Incorrect answer | Total | |
|---|---|---|---|
| Reference group | Ak | Bk | Ak + Bk |
| Focal group | Ck | Dk | Ck + Dk |
| Total | Ak + Ck | Bk + Dk | Nk = Ak + Bk + Ck + Dk |
Table 2 enumerates the number of students with total score k from the reference group who answered the item correctly (Ak) and incorrectly (Bk), and the respective number of students from the focal group (Ck, Dk). The item is not DIF if the odds of answering the item correctly (at a given total score level k) are about the same across focal and reference group, that is, if the odds ratio,  , is close to 1.
, is close to 1.
To account for all total score levels simultaneously, the Mantel-Haenszel estimate of the odds ratio aMH, can be calculated as the weighted average of the odds ratios across the score levels: 
If the item functions the same for different groups for all levels of total score, k, then the odds ratio aMH equals 1, indicating that there is no DIF. For a DIF item that favors the reference group, aMH is greater than 1. When a DIF item favors the focal group, aMH is less than 1.
To test for the presence of DIF, the Mantel-Haenszel  statistic can be calculated as
statistic can be calculated as 

In addition, ∆MH can be assigned to one of three categories: A—negligible difference, B—moderate difference, or C—large difference. At one extreme, category A contains items with ∆MH not significantly different from zero (using a test based on the normal distribution; see Agresti, 2002), or with small effect size,  . At the other extreme, category C contains the items with
. At the other extreme, category C contains the items with  significantly greater than one and large effect size,
significantly greater than one and large effect size,  . Category B consists of all other items.
. Category B consists of all other items.
Significance testing of  or ∆MH results in making multiple comparisons, because every item on the instrument is tested. Therefore, to avoid inflating the type I error rate beyond the nominal level (i.e., minimizing false discoveries of DIF), Kim and Oshima (2013) recommended using the Benjamini-Hochberg p value correction, a sequential multiple comparison procedure employing the Dunn-Šidák adjusted critical p value computation (Benjamini and Hochberg, 1995). This procedure maximizes power while controlling the false discovery rate to the nominal value (typically 5%).
or ∆MH results in making multiple comparisons, because every item on the instrument is tested. Therefore, to avoid inflating the type I error rate beyond the nominal level (i.e., minimizing false discoveries of DIF), Kim and Oshima (2013) recommended using the Benjamini-Hochberg p value correction, a sequential multiple comparison procedure employing the Dunn-Šidák adjusted critical p value computation (Benjamini and Hochberg, 1995). This procedure maximizes power while controlling the false discovery rate to the nominal value (typically 5%).
Methods Using Logistic Regression: Looking Closer at Item Functioning
Another method for detecting DIF for binary-scored items (i.e., 1 = correct and 0 = not correct) proposed by Swaminathan and Rogers (1990) uses logistic regression to model each item individually (see also Zumbo, 1999; Agresti, 2002; Magis et al., 2010). This method predicts the probability that student i answers item j correctly (i.e., Yij = 1), conditional on the total score Xi as follows: 
The two parameters β0j, β1j, describe properties of item j, and they are estimated from the model. Parameter β0j is an intercept, that is, the probability of answering the item correctly for students with a total score of zero (note that if the total score is centered or standardized around zero, then the intercept would indicate the probability of answering the item correctly for students with an average total score). Parameter β1j represents the effect of the total score on the intercept (again, the interpretation of this effect depends on how the total score is scaled), that is, β1j is the effect on the probability of answering each particular item correctly for each one-unit increase in the total score. Note that the model parameters are typically estimated by taking the natural log of the odds of the probability of answering the item correctly, and thus the estimated parameter values given in most software outputs are typically in “logits,” resulting in the model name, “logistic” regression. The estimated logistic regression line relating the total score to the probability of answering the item correctly is often called the item characteristic curve.
To test for DIF, the linear term β0j + β1j * Xi in the logistic regression model 1 needs to be extended by allowing the parameters to differ by group, Gi, as follows: 
The new parameters β0DIF j, β1DIF j describe the potential differences in intercept and slope values between the focal and reference groups (Gi). If neither of these parameter estimates is statistically significant, it is concluded that there is no DIF present in the item (Figure 1A). Estimates of the slopes and intercepts in a logistic regression model are often estimated using iterative weighted least squares (Agresti, 2002). The significance of the parameters involving differences between groups (and thus the detection of DIF) is performed either by comparing the more complex model (which allows groups to differ on the intercept, Figure 1B, or intercept and slope, Figure 1C) with the simpler model (which constrains groups to have the same intercept and slope, Figure 1A) using a likelihood ratio test or by conducting a Wald test on each estimate (see Agresti, 2002). In either case, the Benjamini-Hochberg correction for multiple comparisons would need to be applied to determine the critical p value for detecting DIF.
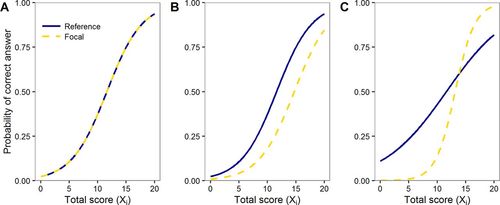
FIGURE 1. Characteristic curves for reference (blue solid) and focal (yellow dashed) group. (A) The shape and placement of the curves are identical, so there is no DIF. (B) The item shows uniform DIF between the reference and focal group. (C) The item shows nonuniform DIF between the reference and focal group: the reference group has the advantage below the total score of 14, and the focal group has the advantage for total scores above 14.
Uniform and Nonuniform DIF.
The logistic regression model allows us to distinguish between two types of DIF: uniform DIF, which affects students at all levels of the total score in the same way (Figure 1B), and nonuniform DIF, which affects students in specific ranges of the total score inconsistently (Figure 1C). If groups only differ significantly on the intercept, that is, if β0 DIF j is nonzero, then the item is said to have uniform DIF. With uniform DIF, the item characteristic curves for the two groups have the same shape and do not cross (Figure 1B). Such items favor one group over another group across the entire range of the total score, albeit less so at the extreme ends of the total score distribution.
However, if groups differ on their slopes (i.e., if β1 DIF j is nonzero), the item is said to have nonuniform DIF. When items have nonuniform DIF, the item characteristic curves for different groups have different shapes, and these curves cross (Figure 1C). Such items favor one group within a specific range of the total score, and then, at some point along the total score distribution, the difference flips to favor the other group.
Shifting from Logistic Regression toward IRT Models
The Two-Parameter Model Reparameterized.
Before explaining IRT models, it is helpful to describe how the basic two-parameter logistic regression model for an item (model 1) can also be fitted using different set of parameters: 
Model 3 differs from model 1 in two ways. First, the standardized total score, Zi, is always used instead of the total score Xi, which makes changes in all parameter estimates that had relied on the total score to become reinterpreted in terms of standard deviations from the mean total score (note that the total score could also be scaled in standard deviations in model 1). Second, and more crucially, instead of the parameters β0j, β1j used in logistic regression, two different parameters, aj, bj, are estimated. The parameters bj and aj describe the difficulty and discrimination of item j, respectively. In this new model, the terms “difficulty” and “discrimination” are used slightly differently than they are usually used in classic measurement theory research (Allen and Yen, 1979), although conceptually they are similar. The difficulty term, bj, is the standardized total scorethat is needed to answer item j correctly with 50% probability. In addition, bj is the inflection point on the item characteristic curve (Figure 2). The discrimination term, aj, is the slope of the curve at the inflection point. We follow the same procedures to test the significance of these terms as was described for the other logistic regression models, using a likelihood ratio test or a Wald test.
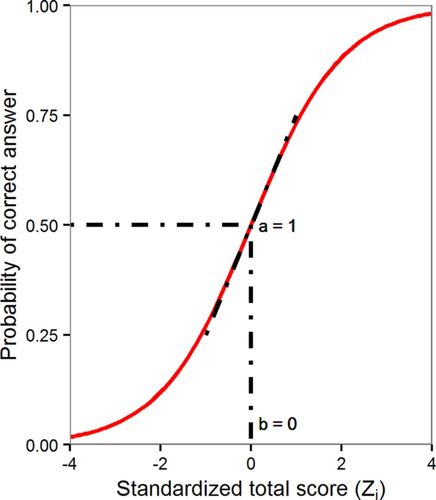
FIGURE 2. Characteristic curve of logistic regression model 3. The line representing the probability of a student answering the item correctly is plotted against the standardized total score (Zi). Parameter b represents difficulty (location of inflection point); parameter a is discrimination (slope).
The Three-Parameter Model: Accounting for Guessing.
The two-parameter logistic regression models discussed so far (models 1 and 3) did not account for the possibility that students may correctly answer an item simply by guessing, which is an expected behavior, especially for multiple-choice tests. To account for guessing, we can extend the two-parameter model (model 3) to include a guessing parameter, cj, as follows: 
Technically speaking, the guessing parameter, cj, actually captures pseudo-guessing, which takes into account the probability of choosing each of the alternative response options (also known as distractors) rather than assuming an equal probability across all option choices. As before, the parameters bj and aj again describe the difficulty and discrimination of jth item, respectively. In the item characteristic curve, the new pseudo-guessing parameter, cj, is represented by the lower asymptote (Figure 3). Note that, for the case where cj is assumed to be 0, the model reduces to the previous two-parameter logistic regression, model 3.
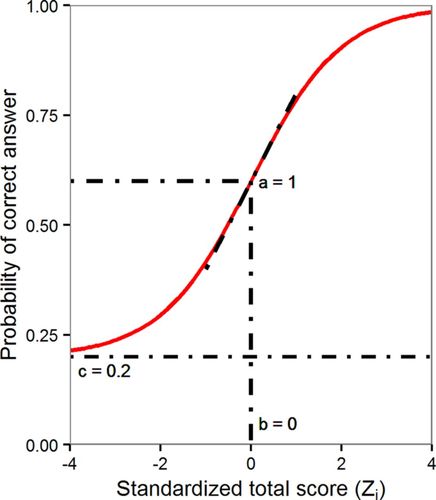
FIGURE 3. Characteristic curve of three-parameter logistic regression model 4. The guessing parameter (c) is the probability that item is guessed without necessary knowledge, and it is represented as the lower asymptote. The inflection point now occurs at the standardized total score, where the probability of the correct answer is (1 + c)/2.
As with our original two-parameter logistic regression that tested for DIF (model 2), we can test the effect of group membership, Gi, on item parameters to determine the presence of DIF by adding the parameters aDIF j and bDIF j to the three-parameter logistic model 4 as follows (Drabinová and Martinková, 2016): 
The new parameters bDIF j and aDIF j are the differences in difficulty and discrimination, respectively, between the focal and reference group, and parameter cj accounts for the possibility of guessing on the jth item. These parameters are estimated using the nonlinear least-squares method, and DIF for each item is detected with an F-test of the submodel (i.e., the model without group membership included) or using likelihood ratio tests (Dennis et al., 1981); as with the other models, the Benjamini-Hochberg correction for multiple comparisons can be applied to control for type I error inflation.
IRT Models: Assuming a Latent Trait
IRT models, sometimes called latent trait models, are similar to logistic regression models in that they also predict the probability of a student answering an item correctly as a function of both the student ability and the item parameters. However, IRT models are more precise, in that students’ true knowledge (theta) is considered latent—or unobserved—because it follows some distribution (e.g., normal) and can only be estimated from performance on observed indicators, in this case items.
The three-parameter logistic IRT model 6 (also called the 3PL IRT model) is analogous to the three-parameter logistic regression model 4, with θ representing the true, unobserved construct level and replacing Z (the standardized observed total score) as 
The interpretation of the item parameters aj, bj, and cj, remains the same as in the three-parameter model 4. However, in IRT models, θ has a specific distribution that is estimated together with item parameters.
Extending IRT Models to Test for DIF.
As with the logistic regression approaches we outlined in models 2 and 4, in IRT models, interactions between group membership G and item parameters bDIF j and aDIF j can be added to the model to test for DIF. The parameters are then estimated jointly for all items simultaneously; this is often done using marginal maximum likelihood (Magis et al., 2010), although other estimation algorithms are possible. Commonly, likelihood ratio tests are used to test whether the model that allows groups to differ on item characteristics fits better than the simpler model that constrains groups to have the same item characteristics (Thissen et al., 1994). In addition, the Wald χ2 test of differences in parameters between groups (Figure 4A) or Raju’s test (Figure 4B) of the differences in areas between groups’ characteristic curves (Raju, 1988, 1990) can be used to evaluate the presence of DIF. We use the Wald test in the case studies presented in this paper and then apply the Benjamini-Hochberg critical p value correction for multiple comparisons.
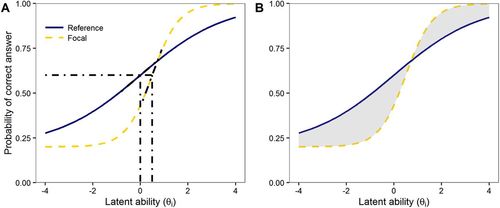
FIGURE 4. IRT methods for detecting DIF. (A) Wald χ2 statistic is based on differences in parameter estimates for the two groups. (B) Raju’s test is based on area between IRT characteristic curves for the two groups.
Other IRT Models.
There are other IRT models as well. First, if the guessing parameter of model 6 is fixed at cj = 0, then the model reduces to what is called a two-parameter IRT model, for which logistic regression model 3 is a proxy. Second, if the discrimination parameter is fixed at aj = 1, in addition to constraining the guessing parameter to 1, then model 6 reduces to a (one-parameter) Rasch model (Rasch, 1960). Each of these two simpler models can also be extended to account for DIF just as outlined above.
Rasch models have recently received a great deal of attention in biology education research, including the recommendation that they be used more frequently for assessment development (Boone, 2016). The biggest advantage of Rasch models, like other IRT models, over the classical test theory models (using only total scores) is that they allow us to estimate the relationship between student ability and all item difficulties. Moreover, this relationship can be visualized using a type of graph known as a person-item map (also called the Wright map).
Although we agree with Boone (2016) in advocating for use of person-item maps (and, in fact, have included a person-item map in our analysis of the HCI; McFarland et al., 2017), we also acknowledge the limits of the one-parameter IRT model: constraining all items to have the same discrimination levels and disallowing for guessing. Hence, we describe the three-parameter IRT model in this paper to afford researchers with a more flexible model that not only provides more information about discrimination and guessing parameters but also allows us to know whether groups differ on these parameters.
Choosing a Model with Sample Size in Mind
One limitation of IRT models is that they require a relatively large sample size. For example, it is recommended that data be collected for 500 students in the reference group and 500 students in each of the focal groups for fitting and calibrating items parameters in the three-parameter IRT model (Kim and Oshima, 2013). Nevertheless, as already mentioned, the strength of two- or three-parameter IRT models is that they can allow for additional information, such as discrimination and guessing, to be estimated and used to inform assessment development (Holland and Wainer, 1993; Camilli, 2006; Zumbo, 2007; Magis et al., 2010).
Software Options
DIF testing using logistic regression analysis (e.g., models 2 and 5) can be carried out in a variety of widely available general statistical analysis software, such as R (R Core Team, 2016), SAS (SAS Institute, 2013), SPSS (IBM, 2013), STATA (StataCorp, 2015), and others. For DIF analysis within an IRT model, there are several commercially available packages, including Winsteps (Linacre, 2005), IRTPRO (Cai et al., 2011), and ConQuest (Wu et al., 1998); for other psychometric software, see www.crcpress.com/Handbook-of-Item-Response-Theory-Three-Volume-Set/Linden/p/book/9781466514393. Although each of these software packages has its own strengths, we note that the Rasch (one-parameter) IRT models are limited to testing uniform DIF due only to their simpler nature (a two-parameter model would be required to test nonuniform DIF). As such, software that estimates two-parameter IRT models is required for testing nonuniform DIF. We also note that the cost of commercially available software can sometimes be a barrier to researchers. Thus, in this paper, we illustrate examples using a freely available and flexible interactive online interface application called ShinyItemAnalysis (Martinková et al., 2017), which was developed within the freely available statistical software environment, R (R Core Team, 2016) and its libraries (e.g., difR, by Magis et al., 2016; difNLR by Drabinová et al., 2017). The Shiny application provides a Web-based graphical user interface that makes it straightforward for users to work with R. The ShinyItemAnalysis package makes use of that interface to provide an easy to implement, user-friendly software for test and item analysis, including detection of DIF (Martinková et al., 2017). We also provide R code for examples from this paper in the Supplemental Material.
CASE STUDIES
We use two data sets to provide context for and illustrate the use of DIF analysis for flagging potentially biased items. These case studies were selected to emphasize the fact that inferences about test fairness based on total scores alone may be misleading. In both case studies, the conclusions that would have been drawn solely from comparing test scores between different groups differ from the conclusions drawn from DIF analysis. Our examples purposefully illustrate two extremes to explain why analyzing total scores is not sufficient for assessing fairness. At one extreme, using a DIF analysis of the HCI (McFarland et al., 2017), we observe a gap in total scores between two groups even though there is no DIF. At the other extreme, we employ a simulated data set to illustrate a case in which the distribution of total scores of two groups is exactly the same, but DIF exists. The simulated data set is a particularly powerful example because it shows that it is theoretically possible to detect DIF even when the distribution of total scores of two groups is exactly the same. This outcome is admittedly improbable, but considering this theoretical possibility helps explicate the strength of DIF analysis. This section ends with a brief overview of other studies that have used DIF analysis in biology, including a discussion of how this result leads to the reformulation of items and, therefore, an assessment that is more equitable and fair.
Case 1: HCI Data Set
The first data set was collected during the final validation of the HCI (McFarland et al., 2017) and illustrates that finding a difference in total score between two groups does not necessarily indicate item bias. The HCI is a 20-item multiple-choice instrument designed to measure undergraduate student understanding of homeostasis in physiology. The HCI was validated with a sample of 669 undergraduate students, out of whom 246 identified themselves as men, 405 identified themselves as women, and the rest did not respond to this question (McFarland et al., 2017). While the overall sample of 669 students is large, we knew that the sample sizes of the two subgroups might be small enough (ns < 500; in each group n < 500) that IRT models would be underpowered.
In the HCI data set, we observed a statistically significant gender gap in total scores, with men performing better (two-sample t test p < 0.01; Figure 5A). The average total score was 12.70 for men (SD = 3.74) and 11.92 for women (SD = 3.55). However, subsequent analysis using the Mantel-Haenszel test, the logistic regression, and the Wald test based on a three-parameter IRT model revealed no significant DIF items (see Supplemental Table 1). We therefore concluded that the HCI test is fair and that the difference between the groups on the total score was due to differences in how women and men understand the concept being targeted (i.e., a true achievement gap), rather than differences in additional content necessary to understand the items. In other words, the gender gap in the total score represents a real difference in understanding, not items that unfairly favor men over women.
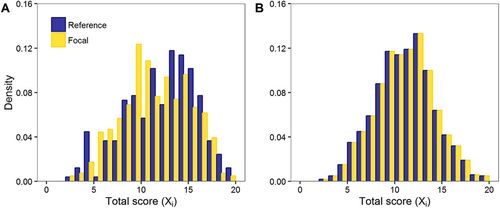
FIGURE 5. Histograms of total score by gender. Men (reference group, blue), women (focal group, yellow). (A) HCI data set. Men achieve higher scores on the HCI as confirmed by statistical tests. (B) Simulated data set based on GMAT item parameters. Distribution of total scores is exactly the same for men and women.
This case study also provides an example of how it can be challenging to fit a three-parameter IRT model to a small sample. For men (n = 246), the initial model yielded unusually large standard errors for parameter estimates for item 17. This was a particularly difficult item based on a common misconception (see also McFarland et al., 2017). But the large standard errors were more likely due to the fact that the sample size was relatively small for such a complex IRT model. In the end, we removed item 17 and then were able to get a good fit with the model.
Case 2: Simulated Data Set
The second data set is a simulated data set of 1000 men and 1000 women taking a 20-item, binary test inspired by Graduate Management Admission Test (GMAT; Kingston et al., 1985, p. 47). This data set was designed to illustrate that DIF items may be present even when different groups have exactly the same distributions of total scores. We generated a data set in which the distribution of total scores was identical for men and women (Figure 5B), even though they performed differently on the first two items of the test. The way in which we constructed this data set (see Supplemental Tables 2 and 3) guaranteed that item 1 would have uniform DIF (Figure 6A) and item 2 would have nonuniform DIF (Figure 6B). The Mantel-Haenszel test, the logistic regression models, and the IRT models all flagged the first two items correctly as DIF (Supplemental Table 4).
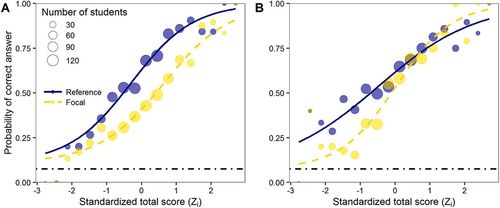
FIGURE 6. Item characteristic curves for reference (blue) and focal (yellow) group by three-parameter logistic regression model 5 for items 1 and 2 in simulated data set. Dots represent the proportion of correct answers on item by the men (reference group, blue) and women (focal group, yellow). Horizontal lines represent the estimate of the guessing parameter, c. (A) Uniform DIF is detected in item 1. (B) Nonuniform DIF is detected in item 2.
Note that this example illustrates item characteristic curves that distinguish between uniform and nonuniform DIF. We specifically used the three-parameter logistic regression (model 5) to generate these curves (Figure 6 and Supplemental Table 4), because we wanted to take into account guessing, as guessing was incorporated into the simulation (see Supplemental Tables 5 and 6). As can be seen in Figure 6, A and B, respectively, item 1 shows uniform DIF and item 2 shows nonuniform DIF.
Comparing the Two Cases
Comparing total scores in the HCI data set suggests there is a difference between men and women in overall test performance (Table 3). However, none of the DIF methods detected any item that functioned differently for women and men. We therefore concluded that the difference in total scores was due to a real gap in how men and women understand the concepts being tested. In contrast, the analysis of the simulated data set demonstrated that, even with exactly the same distribution of total scores for both groups, the test still had items that were not functioning the same way for the two groups (Table 3). Only DIF analysis (rather than total score testing) was necessary to detect this hidden bias. If this had been a real data set, additional item analysis with content experts would be crucial for determining whether the flagged items were fair or unfair.
| HCI | Simulated data set | ||
|---|---|---|---|
| Total scores | Difference | No difference | |
| Men: 12.70, SD = 3.74 | Men: 11.60, SD = 3.11 | ||
| Women: 11.92, SD = 3.55 | Women: 11.60, SD = 3.11 | ||
| p < 0.01 (two-sample t test) | p > 0.99 (two-sample t test) | ||
| DIF | |||
| Mantel-Haenszel | No DIF items (p > 0.05 for all items) | DIF detected in item 1 (p < 0.01) and in item 2 (p < 0.01) | |
| Method does not distinguish between uniform and nonuniform DIF. | |||
| Logistic regression (model 5) | No DIF items (p > 0.05 for all items) | Uniform DIF detected in item 1 (p < 0.01) | |
| Nonuniform DIF detected in item 2 (p < 0.01) | |||
| IRT Wald test (model 6) | No DIF items (p > 0.05 for all items) | Uniform DIF detected in item 1 (p < 0.01) | |
| Nonuniform DIF detected in item 2 (p < 0.01) | |||
| Fairness | No potential unfairness detected | To be determined by content experts |
DIF Analysis in Biology and Beyond: A Brief Review of Other Examples
The statistical detection of DIF is only the first step in evaluating the potential measurement bias. To illustrate the necessity of content experts’ review of the items tagged as DIF, we briefly describe other studies in the biology education literature in which DIF analysis has been used to identify problematic items.
In one study, Federer et al. (2016) explored the relationship between the way men and women answered open-ended questions about natural selection. They used the Mantel-Haenszel test to detect DIF and found that women performed better on questions requiring them to apply key concepts to new situations. They acknowledged that the causes of differences in gender performance are complex and need further study, while also showing evidence that the instrument they developed had little gender bias.
In another study focusing on evolution, Smith et al. (2016) developed an instrument to assess the extent to which high school and college students accept the theory of evolution. Their initial instrument included 14 statements in which students used a four-point rating to indicate their agreement. Two of their items were flagged as DIF, one of which was removed from the next iteration of the instrument. However, the other flagged item (“Evolution is a scientific fact.”) was retained, because it helped distinguish among high school and college students. Smith et al.’s (2016) decision to keep one DIF item emphasizes that the statistical analysis must be paired with evaluation by content experts.
In a somewhat older study, Sudweeks and Tolman (1993) used the Mantel-Haenszel test to detect DIF and also consulted with content experts to identify potential gender-biased items for a 78-item multiple-choice test of scientific knowledge for fifth graders in Utah. The content experts found that one item was potentially biased, because they felt that one of the distractors might favor girls. However, this item was not flagged by DIF analysis. In contrast, the statistical analysis identified eight items as easier for boys and one item that was easier for girls (different than the one flagged by content experts). On the basis of these findings, the authors argued that items require both statistical and content expert analyses for developing assessments.
The consequences of unfair test items can be quite serious. Noble et al. (2012) responded to reports of achievement gaps in a statewide science assessment for fifth graders in Massachusetts, a form of high-stakes testing that resulted from the federal “No Child Left Behind” legislation. As part of their study, they tested DIF on a subset of six items that were flagged by experts by comparing observed item performance with content knowledge ascertained using interviews of children who took the test. Logistic regression revealed that five of the six items were indeed exhibiting DIF (p < 0.01). Students from low-income households and students who were English language learners were more likely to answer these items incorrectly compared with students from higher-income households or students who were native speakers—even when these focal groups had demonstrated in interviews that they correctly understood the science content. Thus, the authors concluded these test five items were unfair and needed to be revised.
In addition to being used to develop and improve instruments, DIF analysis can also be employed to study changes over time among cohorts of a population. As one example, Romine et al. (2016) used logistic regression to detect small differences across time in an assessment of health science interest for middle school students. Three of the items flagged for DIF revealed distinct wording differences compared with other items on the assessment. Indeed, most of the items asked students what they thought of the science they were already engaged in currently, whereas the items flagged for DIF asked students to indicate whether they wanted to spend more time learning science.
In summary, we strongly urge researchers to adopt DIF analysis as part of their routine practice in developing and improving assessments. In addition, we urge researchers to combine statistical analysis with context expertise to best understand whether DIF-flagged items are fair or unfair. This procedure helps ensure that instruments are more fair and equitable when they are first published and, further, that other research using these instruments is also more fair and equitable.
CONCLUSION
In this paper, we argue that DIF analysis is a critical part of developing both large- and small-scale educational tests, because it can be used to assess test fairness and therefore test claims about validity. Comparing the total scores of different groups is helpful to explore how different groups perform, but it is not sufficient for determining fairness. Differences in true scores might exist even in a test that is fair (case study 1). Moreover, potential unfairness of items can be hidden and not revealed by total score analysis (case study 2).
We have also provided a brief tutorial of some of the most common methods for DIF analysis, and this tutorial is supplemented with selected R code and an interactive online application (Supplemental Material; Martinková et al., 2017, see also https://shiny.cs.cas.cz/ShinyItemAnalysis). As with any active area of research, more methods are available and new methods are still being proposed (e.g., Magis et al., 2014; Berger and Tutz, 2016). Deciding which method to use depends on sample sizes and assumptions about items. Closer guidance may be provided by simulation studies in which data sets are generated thousands of times. This approach allows the properties of different DIF detection methods to be compared with respect to their power and type I error rate (e.g., Swaminathan and Rogers, 1990; Narayanan and Swaminathan, 1996; Güler and Penfield, 2009; Kim and Oshima, 2013; Drabinová and Martinková, 2016). Studies like these have demonstrated that the Mantel-Haenszel method works particularly well for small sample sizes but, as expected from its formula, does not always detect nonuniform DIF (Swaminathan and Rogers, 1990; Drabinová and Martinková, 2016). In our opinion, the methods that are based on regression are particularly appealing, because they are more flexible in detecting both nonuniform and uniform DIF and, unlike the Mantel-Haenszel method, also provide parameter estimates (Zumbo, 1999). Finally, IRT models have an added advantage of providing more precise estimates of latent traits, but they may be difficult to fit for sample sizes less than 500 students per group (e.g., Kim and Oshima, 2013).
We wish to reemphasize here that items flagged as DIF only have the potential to be unfair; an expert review is required (for methods, see, e.g., Ercikan et al., 2010; Adams and Wieman, 2011) to determine whether the differences in performance among groups are due to factors related to the concept being tested, or whether they are instead “unfair” and related to a secondary latent trait, such as cultural, curricular, or language-related knowledge.
While DIF analysis is ubiquitous in large-scale assessment, it has been used rarely as a check for fairness in developing and using low-stakes tests that are used daily in all levels of education. However, developing fair tests is a value that all educators should aspire to in order to ensure that tests are not only accurate for student feedback, but also for informing modifications to teaching. Moreover, fair tests are necessary to promote and retain underrepresented groups in science, technology, engineering, and mathematics fields (Rauschenberger and Sweeder, 2010; Creech and Sweeder, 2012; Legewie and DiPrete, 2014). In short, DIF analysis should have a routine role in all our efforts to develop assessments that are more equitable measures of scientific knowledge.
ACKNOWLEDGMENTS
This research was supported by Czech Science Foundation grant number GJ15-15856Y and by National Science Foundation grant number DUE-1043443. We thank Ross H. Nehm, Roddy Theobald, Mary Pat Wenderoth, and two anonymous reviewers for their valuable feedback.