Teaching Hardy-Weinberg Equilibrium using Population-Level Punnett Squares: Facilitating Calculation for Students with Math Anxiety
Abstract
Hardy-Weinberg (HW) equilibrium and its accompanying equations are widely taught in introductory biology courses, but high math anxiety and low math proficiency have been suggested as two barriers to student success. Population-level Punnett squares have been presented as a potential tool for HW equilibrium, but actual data from classrooms have not yet validated their use. We used a quasi-experimental design to test the effectiveness of Punnett squares over 2 days of instruction in an introductory biology course. After 1 day of instruction, students who used Punnett squares outperformed those who learned the equations. After learning both methods, high math anxiety was predictive of Punnett square use, but only for students who learned equations first. Using Punnett squares also predicted increased calculation proficiency for high-anxiety students. Thus, teaching population Punnett squares as a calculation aid is likely to trigger less math anxiety and help level the playing field for students with high math anxiety. Learning Punnett squares before the equations was predictive of correct derivation of equations for a three-allele system. Thus, regardless of math anxiety, using Punnett squares before learning the equations seems to increase student understanding of equation derivation, enabling them to derive more complex equations on their own.
INTRODUCTION
Population genetics is a topic often taught in undergraduate introductory biology courses to connect student understanding of Mendelian inheritance to more abstract principles of evolutionary processes (Ortiz et al., 2000; Brewer and Gardner, 2013). This instruction frequently focuses on the Hardy-Weinberg (HW) principle (i.e., the null hypothesis that allelic frequencies do not change in a population in the absence of evolution) and the accompanying HW equations (p + q = 1 and p2 + 2pq + q2 = 1) to predict the relationship between allelic and genotypic frequencies (Hardy, 1908; Weinberg, 1908). While there is widespread acknowledgment that the HW principle is valuable for student understanding of evolution (Mertens, 1992; Ortiz et al., 2000; Brewer and Gardner, 2013), it is also recognized that many students struggle with the quantitative and abstract nature of HW calculations (Ortiz et al., 2000; Carlton et al., 2004; Masel, 2012).
One common complaint with current methods of teaching HW equilibrium is that the emphasis on calculation undermines student understanding of the biological principles behind it, that is, students get caught up in the math and miss the biology (Mariner, 1973; Masel, 2012; Brewer and Gardner, 2013). The amount of time that instructors invest in helping students with their calculation skills displaces time that instructors could be using to help students better understand the biological principles behind these equations, such as the mechanisms of evolutionary change. However, quantitative reasoning itself is also an important core competency that all biology students should be taught, as noted in the American Association for the Advancement of Science report Vision and Change in Undergraduate Biology Education (AAAS, 2011). As the life sciences become more and more integrated with and dependent on quantitative tools, these skills should be integrated throughout biology curricula rather than removed (Gross, 2000; Bialek and Botstein, 2004), and evidence suggests this can be done successfully even at the introductory level (Bray Speth et al., 2010; Thompson et al., 2010; Madlung et al., 2011; Hoffman et al., 2016). Thus, pedagogical practices are needed to teach quantitative topics effectively so the math is retained but does not overshadow important biological principles.
Barriers to Success with HW Equilibrium
Difficulties with HW calculations may arise for various reasons. First, students may lack the skills to perform the calculations. Instructors perceive that students with low conceptual understanding of probability (Masel, 2012) or lack of algebraic skills (Winterer, 2001) may have a hard time with HW calculations. Research suggests that, when students struggle with quantitative topics in science, it can either be due to a lack of mathematical knowledge and preparation or a failure to apply that mathematical knowledge in a novel context (Tuminaro and Redish, 2004; Scott, 2016). Thus, students with the poorest mathematical background will likely struggle the most with HW calculations, but even students with strong calculation skills may still have difficulties using those skills in the unfamiliar territory of population genetics (see also Selden et al., 2000; Cui et al., 2006; Redish and Gupta, 2009).
Second, challenges with HW equilibrium are likely common in students with high levels of math anxiety (Stencel, 1991; Brewer and Gardner, 2013), which is a construct that describes a general negative affect toward mathematics (Hembree, 1990). Math anxiety has been associated with a decrease in mathematical performance, likely because of an impairment in working memory, problems with number processing, avoidance behavior (and thus loss of math practice), or a combination of all three (Ashcraft and Kirk, 2001; Ashcraft, 2002; Miller and Bichsel, 2004; Buelow and Frakey, 2013; Foley et al., 2017; Skagerlund et al., 2019). Interestingly, many studies have found that females are more likely to experience math anxiety compared with males, which may contribute to gender gaps in participation in science (Hembree, 1990; Miller and Bichsel, 2004; Rubinsten, Bialik, and Solar, 2012). Lyons and Beilock suggest that interventions aiming to control negative emotions associated with math may be more effective than simply increasing math training, because many individuals with math anxiety already have the skills necessary to perform the calculations (Lyons and Beilock, 2012a). The authors further show that the anticipation of doing math, rather than the actual performance of math itself, is associated with neural activity in brain regions associated with threat detection and even the experience of pain in individuals with high math anxiety (Lyons and Beilock, 2012b).
Pedagogical Efforts to Overcome Barriers
Common approaches to help students overcome barriers to master HW equilibrium specifically can be found in the literature, including the use of computers or computer simulations to perform the calculations for students (Mariner, 1973; Carlton et al., 2004), the use of classroom exercises where students simulate populations (Winterer, 2001; Bray Speth et al., 2010; Brewer and Gardner, 2013), and the use of population Punnett squares (PSs) to visually predict the probability of different genotypes in the next generation (Stencel, 1991; Mertens, 1992; Ortiz et al., 2000). Although lesson plans have been published with such suggestions on how to teach this topic, there are no studies, to our knowledge, that specifically test these strategies to determine whether they are effective at helping students understand HW equilibrium. A recent analysis of the literature also found that less than 25% of the articles about instructional strategies for teaching evolution topics actually included experimental data (Ziadie and Andrews, 2018), so more empirical studies are needed in this area generally. We chose to focus on population Punnett squares for reasons outlined in the following section.
Theoretical Rationale for Population Punnett Squares
While there are various ways of using population PSs, we specifically wanted to use a population PS to teach HW equilibrium both as 1) a visual representation of random mating in a population in a way that was familiar to students after already completing a unit on inheritance and 2) a calculation aid to help students perform the mathematics traditionally done using the HW equations (see Supplemental Material for visuals). The PS could be used completely independent of the classic p and q variables (to act as a calculation aid that stands alone) or as a scaffold in conjunction with the p and q variables (to derive the HW equations or act as a calculation aid that includes the classic symbols). We would like to emphasize that this population PS approach still requires students to perform the same calculations as are dictated by the HW equations (including exercises that require rearrangement of the equations, or “thinking backward” from offspring to parents). Thus, the requirement for mathematical calculation is not eliminated. Accordingly, we would not necessarily expect PS instruction to help students overcome lack of math skills. Rather, students are using the HW equations without realizing it (see example assessment items solved using either the classic HW equations or a population PS on p. 16 of the Supplemental Material). Then, if students are later introduced to the equations, including p and q variables, the symbols and expressions should already have meaning for the students and thus may be better understood.
We purposefully chose population PSs in an attempt to help students overcome math anxiety as a barrier to success with HW equilibrium. Evidence suggests that the anticipation (rather than the execution) of math could be the trigger for math anxiety (Lyons and Beilock, 2012a,b), so we wanted to focus on the way students are introduced to the mathematical calculations and/or equation derivation. Because a population PS would “look” more like biology than math to the students and PSs were used previously in the inheritance unit, we hypothesized that initially using population PSs as a visual scaffold for mathematical calculations would elicit less math anxiety in students than if they derived and used formal equations right away. We predicted that, without math anxiety to consume working memory (Ashcraft and Kirk, 2001), students who normally experience high math anxiety would be better able to perform calculations, understand what the calculations represent biologically, and derive the equations later if taught the PS method first.
Research Questions
We tested the effectiveness of PS instruction in the population genetics unit of an introductory biology course using a quasi-experimental, crossover study design. We first compared the effects of population PS instruction with classic equations (EQ) directly, then tested the order of instruction if students learned both methods. We focused on the following research questions:
Does PS instruction affect HW calculation proficiency compared with classic EQ instruction? Is this effect dependent on student math anxiety?
If both methods are taught, does the order of instruction affect the work type (PS vs. EQ) students choose to use? Does this effect on work type depend on student math anxiety?
If both methods are taught, does the order of instruction affect calculation proficiency?
If both methods are taught, does the work type students choose (PS vs. EQ) affect calculation proficiency? Is this effect dependent on student math anxiety?
If both methods are taught, does the order of instruction affect students’ understanding of HW equilibrium and the derivation of the HW equations? Is this effect dependent on student math anxiety?
METHODS
Ethics Statement
The study design was reviewed and approved by the Institutional Review Board at Brigham Young University. All research subjects gave written consent to participate in the study.
Course Description and Participants
This study was conducted in an introductory biology course for nonmajors, taught at a private university with an enrollment of ∼30,000 students. This course is often taken to fulfill a general education requirement and has no prerequisites. The course curriculum includes topics concerning the nature of science, chemistry, cell and molecular biology, genetics, evolution, and ecology. By the time of the unit on HW equilibrium, all students had already been taught to use PSs to solve genetics problems (see placement in course in Figure 1). Instructional methods included interactive lecture with frequent formative assessment, clicker questions, and think–pair–share.
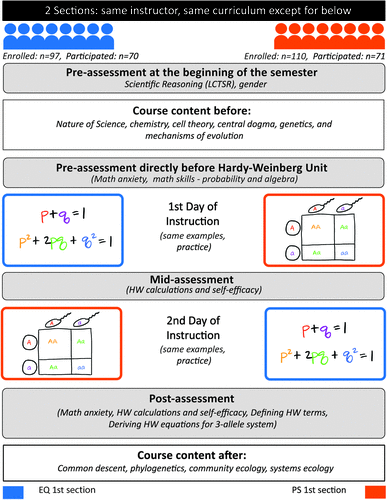
FIGURE 1. Quasi-experimental study design. Two sections of an introductory course for majors had the same curriculum, except for 2 days of instruction about HW equilibrium during the second half of the semester. The EQ 1st section started with equation derivation and usage, then learned population PSs on day 2. The PS 1st section had the treatments in the reverse order. Both sections had the same examples and practice problems used in class on day 1 and on day 2. Assessments used for data collection are shaded in gray.
Two sections of this course were used in this study. Students registered for the course section of their choice, and each section met separately (one at 10 am and one at 11 am). The section that started with equation derivation (“EQ 1st section”; see Figure 1) had 97 students enrolled, with 70 students both consenting to participate in the study and completing the mid-assessment. The section that started with PSs (“PS 1st section”) had 110 students enrolled, with 71 students both consenting to be participants and completing the mid-assessment. Some measures have sample sizes lower than 70 and 71 because students failed to take an assessment or answer a specific question. We always included as many students as possible to maximize sample sizes and avoid bias, so sample sizes change slightly from analysis to analysis for this reason. Thus, sample sizes are listed with each figure or analysis.
Experimental Design
Because students self-selected into course sections, we employed a quasi-experimental approach (see Figure 1). To limit variability between sections, both sections were taught in the same room, by the same instructor (author E.G.B.), during the same semester; using the same curriculum, homework assignments, and exams; and having the same teaching assistants. Learning activities and instructional methods were consistent between sections, with the exception of the described treatment shown in Figure 1. We recognize that having an author of this study instruct the course has the potential to add bias. We strove for researcher neutrality by incorporating good teaching practices into both treatments and have included all relevant lesson plans in the Supplemental Material to show the differences between sections.
Because students could not be sorted randomly into the two sections, we assessed equivalency of the student populations in each section with a pre-assessment at the beginning of the semester (assessing scientific reasoning skills upon course entry) and a pre-assessment directly before the treatment (investigating levels of math anxiety and mastery of math skills; see Figure 1). Instruction about HW equilibrium was then given over two class sessions. In the first class session, one section derived the HW equations to solve HW problems, while the other section was taught to use a population-level PS to solve HW problems (see Supplemental Material for lesson plans). The two sections solved the exact same practice problems, but they used different methods. After the first day of instruction (having been taught only one method), students from both sections completed an assessment evaluating their ability and confidence in solving HW problems (see “Mid-Assessment” in the Supplemental Material). On the second day of instruction, each section received the opposite treatment: the section that was taught the equations first was now taught how to use a population PS to model HW equilibrium, while the section that had learned to use a population PS derived the HW equations (see Supplemental Material for lesson plans). Again, sections were given the same practice problems but just used a different method to solve them. After the second day of instruction (with all students now having been taught both methods), a final instrument was administered assessing students’ ability to solve HW problems, understanding of the biological meaning of the HW equations, ability to derive more complex HW equations, math anxiety at the end of the unit, and other attitudes (see “Post-Assessment” in the Supplemental Material).
Due to the crossover design of the study, the results of the mid-assessment and the post-assessment can be used to answer different experimental questions. The mid-assessment, given after the first day of instruction, allowed for direct comparison of the two instructional methods and was used to address research question 1. The post-assessment, given after the second day of instruction, was used to investigate the effect of the order of instruction (research questions 2–5).
Instruments and Data Collection
Scientific Reasoning.
We used the 24-item version of the Lawson Classroom Test of Scientific Reasoning (LCTSR; Lawson, 1978; Lawson et al., 2000) to assess content-independent scientific reasoning ability. We chose this instrument because we wanted to assess students’ level of reasoning without measuring any kind of domain-specific preparation. Validity of this instrument has been established previously for college student populations, verifying that the tasks do not require domain-specific knowledge (Lawson et al., 2000). A more recent study of U.S. college freshmen also verified the LCTSR’s validity as a unidimensional construct of scientific reasoning, and the authors demonstrated high internal consistency (Cronbach’s alpha = 0.85) with the scoring method we used (Bao et al., 2018). This instrument was administered to students on the pre-assessment at the beginning of the semester (see Figure 1).
Math Anxiety.
We chose to use the Abbreviated Math Anxiety Survey (AMAS; Hopko et al., 2003) to assess math anxiety, because it was brief and specifically developed for undergraduate students. It was previously shown to have strong internal consistency (Cronbach’s alpha = 0.9), test–retest reliability (r = 0.85), and convergent/divergent validity (r = 0.85 with the longer Math Anxiety Rating Scale–Revised instrument) with college students (Hopko et al., 2003).
The AMAS consists of nine questions (available in the Supplemental Material), and respondents were asked to rate each math task with a level of anxiety from one to five (low anxiety to high anxiety). Student responses were then summed for all nine questions to give a total “anxiety score” (ranging from 9 to 45). For some analyses, we categorized students into three categories: low, moderate, or high anxiety. We defined “low anxiety” as reporting an anxiety score of 18 or lower (equivalent to marking low or some anxiety on all items), “moderate anxiety” for scores of 19–27 (e.g., marking some or moderate anxiety on all items), and “high anxiety” as an anxiety score above 27 (e.g., moderate anxiety or higher on all items). The highest score we obtained was 36. In all regression analyses, raw math anxiety score was used to give more information. This instrument was administered to students on the pre-assessment directly before the HW unit and on the post-assessment after the HW unit (see Figure 1).
Math Skills.
Pretreatment math skills were assessed using a six-item instrument that required students to solve open-response mathematics problems. This instrument was created in two steps. First, we identified key mathematical ideas involved in HW equilibrium and equations, such as basic probability, probabilities regarding independent events, and solving with equations. We then took these mathematical ideas and referenced the mathematics education research literature to create specific items to test those ideas (e.g., Sfard, 1991; Sfard and Linchevski, 1994; Lecoutre, 1992; Lecoutre and Fischbein, 1998; Panizza et al., 1999; Shaughnessy and Ciancetta, 2002; Batanero and Sanchez, 2005). For example, we created separate questions for probabilities associated with independent events when those events produce the same outcomes or different outcomes (Lecoutre, 1992; Lecoutre and Fischbein, 1998; Shaughnessy and Ciancetta, 2002). We also created a question to assess whether students conceptualized terms within an equation (or groups of terms) as their own entities (Sfard, 1991; Sfard and Linchevski, 1994). The math skills assessment is provided in the Supplemental Material, along with validity justifications for each open-response question. This instrument was administered to students on the pre-assessment before the population genetics unit (see Figure 1).
HW Calculations and Work.
On both the mid-assessment (after day 1 of instruction) and the post-assessment (after day 2 of instruction; see Figure 1), we tested students’ ability to perform calculations for populations assumed to be in HW equilibrium. Students were asked to calculate allelic, genotypic, or phenotypic frequencies given a different allelic, genotypic, or phenotypic frequency for a population. This required correctly identifying the frequencies that were given and understanding the mathematical relationships between frequencies. There were six unique questions, three given on the mid-assessment and three on the post-assessment. All test items were multiple-choice format and can be found in the Supplemental Material.
Students were also asked to show work for all calculations. Two researchers (K.R.W., A.B.) independently coded student work into one of three categories: included a population PS in their work (“PS,” students may or may not have still done calculations outside the PS), only performed calculations using the HW equations (“EQ,” students may or may not have used the p and q variables), or showed no work at all (“NW”). The two researchers agreed for 98.1% of mid-assessment items (Cohen’s kappa = 0.97). Generally, differences in coding arose from confusion about whether or not to count a PS if it had been crossed out or erased. We decided that even crossed-out or erased PSs would be counted in the PS category (because they were evidence that students used the PS as they thought through the problem), and this led to unanimous agreement on final categorization. Student work on the post-assessment was coded in the same way (initial coding by two raters, K.R.W. and A.B., yielded 99.5% agreement and Cohen’s kappa = 0.98; the two raters then came to agreement). The percent of the time students used a type of work was calculated by taking the number of questions on which students used a particular type of work and dividing it by the total number of questions.
Self-Efficacy.
Students’ feelings of self-efficacy were assessed by self-reported confidence in their HW calculation proficiency on a five-point Likert scale (1 = no confidence, 5 = complete confidence). The full wording of this question can be found in the Supplemental Material. Because we assessed self-efficacy using this single item on the mid-assessment and again on the post-assessment (see Figure 1), the lack of validity of this construct is a limitation of our study.
Conceptual Understanding of HW Equilibrium and Equations.
We attempted to assess students’ understanding of HW equilibrium and its associated equations in three different ways on the post-assessment (see the Supplemental Material). First, we gave students an open-response question to derive HW equations to model a three-allele, diploid system given the variables p, q, and r while showing their work. We graded this question as number of equations correct: 0, 1, or 2. Equations had to be exactly correct to count as “correct.” Two raters (K.R.W., AB) independently coded student work used into two categories: drew a 3 × 3 PS or did not. Initial coding yielded 96.3% agreement (Cohen’s kappa = 0.92), and then a third rater (E.G.B.) looked at disagreement and decided whether there was a PS or not.
As a second way to assess understanding, we asked students to explain why the mathematical model of HW equilibrium would no longer hold if one of its assumptions were to be violated. Two researchers (S.R.W., R.F.G.) coded all responses along four separate dichotomous categories: 1) whether or not the student’s response included a correct mathematical explanation, as opposed to speaking strictly in biological terms or including an incorrect mathematical explanation; 2) whether or not the student drew or referred to a PS in any way; 3) whether or not the student wrote the classic HW equations or referred to p/q variables; and 4) whether or not the student attempted to write an altered HW equation of some kind (e.g., if mutation occurred, p + q + r = 1 rather than p + q = 1; or if homozygous recessive offspring would not survive past birth and thus were selected against, p2 + 2pq = 1 rather than p2 + 2pq + q2 = 1). First, the two researchers coded separately, with initial coding yielding 93.5% agreement (Cohen’s kappa = 0.77), but then they came to agreement on all after discussion.
As a third way to assess understanding, we asked students to define each term of the HW equations (p, q, p2, 2pq, q2) in biological terms. We first had two researchers (K.R.W., A.B.) independently code each definition to determine whether or not the student was defining the correct biology entity. Initially, coders reached 87% agreement (Cohen’s kappa = 0.48). We then went through the differences and determined that most of them arose from disagreement about how stringent to be about the use of “allele,” “gene,” “genotype,” and “trait” (e.g., some students would define the variable correctly but add on the word phenotype when it was not needed). We decided to be lenient with such cases as long as we could tell they were referring to the correct entity. Raters then came to unanimous agreement. Coding for the combined term p2 + 2pq was slightly different. Two researchers (K.R.W., A.B.) classified definitions into the following three categories: a correct response that included the overarching idea of a phenotype, a correct response that focused on the sum of two genotypes rather than a shared phenotype, or incorrect. When we compared the two raters’ classifications into these three categories, we found 88.8% agreement and Cohen’s kappa = 0.78. The raters then came to unanimous agreement. These three categories were treated as a nominal variable in analyses (not ranked).
Instruction Preference.
After both days of instruction, we asked students which day of instruction they found most helpful for their learning (single-choice question, EQ or PS day). Unfortunately, some students did not follow instructions and handwrote “both” instead of choosing the EQ day or the PS day. For the analysis, we only included students who picked a day as their preference. See this question in the post-assessment in the Supplemental Material.
Statistics
We first compared our two groups (EQ 1st vs. PS 1st) directly using simple statistical tests as described in the text. Due to our quasi-experimental approach, we then used multiple linear (ordinary least-squares) regression to predict outcome variables using various student characteristics in addition to experimental treatment (Theobald and Freeman, 2014). For each regression analysis, we verified that no assumptions of linear regression were violated. While some student characteristics were correlated (math anxiety and math skills, reasoning scores and math skills, etc.), correlation coefficients were all less than 0.5. Furthermore, variance inflation factor values were always between 1.07 and 1.56, suggesting that we did not have any issues with multicollinearity. Furthermore, when interactions were included in multiple linear regression, variables were centered around their mean before interaction terms were calculated to avoid multicollinearity with their component variables.
Our sample size was constrained by the number of students who enrolled in the course and consented to participate in the study. A priori power analyses estimated that, with our sample size (n = 141 overall, or n = 138 in analyses that included LCTSR scores), we would have high statistical power (0.8 or higher) to detect medium effect sizes. Thus, small effects could possibly be undetectable with our data set, and any small effects we would detect would likely have inflated effect sizes (Ioannidis, 2008). We comment on this limitation of our study in the Discussion section.
Student characteristics used in the regression analyses were restricted to those that theoretically should impact HW calculations (math anxiety, math skills, and scientific reasoning) and any that differed between course sections. Our regression analyses included seven or eight predictors depending on the analysis. This allowed for 17–20 subjects per variable, which is considered appropriate for detecting medium effect sizes (Green, 1991) and more than sufficient for estimating the magnitude of regression coefficients and their confidence intervals (Austin and Steyerberg, 2015). In our a priori power analyses, further restriction of the number of independent variables in our regression analyses did not increase power substantially enough to allow us to detect small effects (see also the recommendations in Green, 1991), so we chose to just provide our full regression models in the text rather than performing model selection.
All statistical analyses were conducted using IBM SPSS Statistics v. 27. Figures were generated using GraphPad Prism v. 9.0.0. All error bars represent standard error of the mean.
RESULTS
Section Equivalence
Because our experiment is only quasi-experimental (students chose the section in which they wanted to enroll), we first investigated whether the two course sections were equivalent in terms of preparation and demographics. As summarized in Table 1, mean scores on pretreatment math skills (probability and algebra), math anxiety, and scientific reasoning were indistinguishable between the two sections, as were student gender ratios. Sections did differ in terms of school year, as the section that was taught the equations first had more juniors and seniors, while the section that was taught the PS method first had more freshmen and sophomores (see Table 1). They also differed in terms of proportions of science, technology, engineering, and mathematics (STEM) versus non-STEM majors; the section that learned the PS method first had more STEM majors than the other section (see Table 1). We wondered whether these two differences were related, for example, that non-STEM majors were more likely to be older, but there was no relationship between school year and major; χ2(3) = 0.044, p = 0.998, n = 141.
| Variable | EQ 1st | PS 1st | Statistical test: test statistic, p, effect sizea | ||||
|---|---|---|---|---|---|---|---|
| M | SD | N | M | SD | N | ||
| Math skillsb,c | 4.2 | 1.1 | 70 | 4.3 | 1.1 | 71 | Independent-samples t: t(139) = 0.44, p = 0.66, Hedges’ g = 0.07 |
| Math anxietyb,d | 19.6 | 5.6 | 70 | 20.4 | 6.6 | 71 | Independent-samples t: t(139) = 0.80, p = 0.43, Hedges’ g = 0.13 |
| Reasoninge,f | 19.6 | 3.0 | 68 | 18.7 | 4.5 | 70 | Welch’s t: t(122) = 1.42, p = 0.16, Glass’s Δ = 0.21 |
| School yearg,h | 2.5 | 0.9 | 70 | 2.2 | 0.8 | 71 | Mann-Whitney U: U = 2017, p = 0.03, Cohen’s d = 0.36 |
| Gendere | 42 mal, 28 fem | 43 mal, 28 fem | Chi-square: χ2(1) = 0.005, p = 0.95, φ = 0.006 | ||||
| Math anxietyi | 31 L, 31 M, 8 H | 31 L, 29 M, 11 H | Chi-square:χ2(2) = 0.533, p = 0.77, φ = 0.061 | ||||
| Majorg | 25 STEM, 45 not | 38 STEM, 33 not | Chi-square: χ2(1) = 4.52, p = 0.03, φ = 0.18 | ||||
As noted in the Methods section, we did not have the statistical power to confidently detect small effects, and all differences between sections were either insignificant or small (Table 1, Cohen’s d < 0.5; Cohen, 1988). Thus, there could be small differences we did not detect, and the effect sizes for significant effects could be exaggerated (Ioannidis, 2008). In an effort to account for differences that already existed in our two student populations, we wanted to include student characteristics as possible predictors in later regression models (Theobald and Freeman, 2014). We decided to include all variables that significantly differed by section (STEM major and year in school) plus those we had initially predicted would affect success with HW calculations based on theory (scientific reasoning, math anxiety, and math skills).
Research Question 1
Does PS instruction affect HW calculation proficiency compared with classic EQ instruction? Is this effect dependent on student math anxiety? The first three items on the mid-assessment required students to calculate frequencies of variables assuming a population was in HW equilibrium. We coded student work on each problem according to the method they used: including a population PS (“PS”), showing calculations and equations but no PS (“EQ”), or showing no work at all (“NW”). The number of problems on which students used a PS differed by section, independent-samples t test with Welch’s correction, t(121.5) = 13.4, p < 0.0005, EQ n = 70, PS n = 71, with a majority of students in both sections using the method that they had been taught in class as expected (Figure 2A).
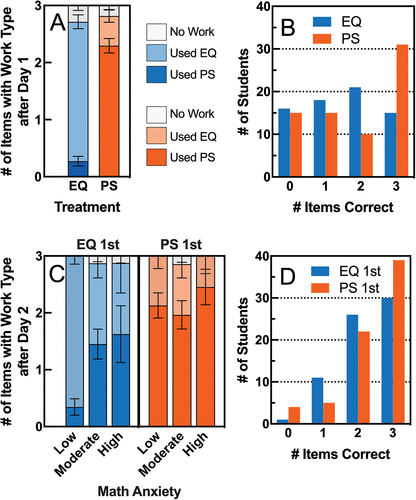
FIGURE 2. Performance on HW calculation problems. (A) The work students used (PS, EQ, or no work) was coded for each of three HW calculation questions on the mid-assessment. The average number of problems for each type of work is shown here by treatment (EQ: n = 70; PS: n = 71). (B) Frequencies of mid-assessment scores are shown by treatment. (C) Post-assessment work used was calculated as in A and shown by treatment order and math anxiety (EQ 1st: Low n = 31, Moderate n = 31, High n = 8; PS 1st: Low n = 31, Moderate n = 29, High n = 11). (D) Frequencies of mid-assessment scores are shown by treatment (EQ 1st: n = 68, PS 1st: n = 70).
As shown in Figure 2B, the section that learned the population PS method scored higher on this assessment (M = 1.8, SD = 1.2, n = 71) than the EQ section (M = 1.5, SD = 1.1, n = 70), but this raw difference was not significant by independent-samples t test, t(139) = 1.57, p = 0.12, or Mann-Whitney U-test (because data were not normally distributed), U = 2877.5, p = 0.09. Next, we used multiple linear regression to target student performance (no. correct) on these HW calculation items, with possible predictors including STEM major and year (because these differed between sections); reasoning, math skills, and math anxiety (because these should theoretically impact student calculation proficiency); with treatment (EQ vs. PS) and an interaction between treatment and math anxiety (our experimental questions). Model results are shown in Table 2. Students’ math skills, scientific reasoning (LCTSR), and math anxiety were all significant predictors of increased calculation proficiency, as expected. Teaching the PS method also significantly predicted an additional 0.33 questions correct, although the effect was small and only accounted for 1.4% of variation in scores. This effect could not be explained by there being younger students or more STEM majors in that section, because year in school and major were both included in the model. Finally, there was not a significant interaction between instruction and math anxiety (Table 2).
| R2 | Adjusted R2 | Variable | B | SEB | β (standardized) | p value | ω2 a |
|---|---|---|---|---|---|---|---|
| 0.393 | 0.360 | (Intercept) | −0.544 | 0.705 | 0.442 | ||
| Math skills | 0.375 | 0.085 | 0.356 | <0.0005 | 0.086 | ||
| Reasoning (LCTSR) | 0.068 | 0.025 | 0.226 | 0.007 | 0.030 | ||
| Math anxiety | −0.032 | 0.015 | −0.167 | 0.036 | 0.016 | ||
| Taught PSsb | 0.335 | 0.166 | 0.145 | 0.046 | 0.014 | ||
| Year | −0.128 | 0.097 | −0.094 | 0.187 | 0.004 | ||
| STEM majorc | 0.128 | 0.168 | 0.055 | 0.446 | −0.002 | ||
| Taught PSs * math anxiety | −0.012 | 0.027 | −0.032 | 0.656 | −0.004 |
Interestingly, the PS section outperformed the EQ section only on the first question of the mid-assessment (Fisher’s exact test: p = 0.011, odds ratio = 2.45, n = 141; see Supplemental Material for questions), while the two sections performed equally on the second and third questions (Fisher’s exact test: p = 0.60 and 0.74, respectively, n = 141 for both). The differential performance by treatment on the first question cannot be explained by pre-existing group differences (proportion of STEM majors) as both non-STEM and STEM majors were more likely to get the first question on the mid-assessment correct if they received PS instruction (see Supplemental Figure S1).
Students’ feelings of self-efficacy in solving HW problems after 1 day of instruction were assessed by self-reported confidence. The PS 1st section reported somewhat higher confidence (small to medium effect size), but the distributions of the two sections’ confidence levels were indistinguishable by the Mann-Whitney U-test (U = 2831.5, p = 0.13, Cohen’s d = 0.26; EQ 1st: M = 2.90, SD = 1.02, n = 70; PS 1st: M = 3.14, SD = 0.96, n = 71).
Research Question 2
If both methods are taught, does the order of instruction affect the work type (PS vs. EQ) students choose to use? Does this effect on work type depend on student math anxiety? We again coded student work for each of the three HW calculation problems (PS, EQ, or no work). As shown in Figure 2C, there was more diversity in the work used compared with the mid-assessment, but the majority of students still used the method that they were taught first. Two-way ANOVA results suggest that treatment order (p < 0.0005, ω2 = 0.10), math anxiety category (p = 0.02, ω2 = 0.03), and an interaction between the two (p = 0.02, ω2 = 0.04) all significantly explained variance in the use of PS work (adjusted R2 = 0.22; EQ 1st n = 68, PS 1st n = 70; Figure 2C).
High-anxiety students used PS work much more than low-anxiety students in the EQ 1st section (blue, Figure 2C) but not in the PS 1st section (orange). Specifically, moderate- and high-anxiety students in the EQ 1st section abandoned the EQ method after being taught the PS method, but low-anxiety students in the PS 1st section did not abandon the PS method in favor of the EQ method.
To account for differences between sections (year in school and STEM major) and other variables that could impact work type used (reasoning and math skills), we performed multiple linear regression with %PS work as the target. In this analysis, actual math anxiety score was used as a predictor rather than math anxiety category, providing more information. As shown in Table 3, instruction order, math anxiety, and an interaction between the two were still significant predictors of PS use. Learning about PSs first was predictive of using PS work on one more question compared with those who learned EQ first, a medium-sized effect. In addition, upper-level students were less likely to use PS work.
| R2 | Adjusted R2 | Variable | B | SEB | β (standardized) | p value | ω2 a |
|---|---|---|---|---|---|---|---|
| 0.294 | 0.256 | (Intercept) | 0.259 | 0.306 | 0.399 | ||
| Taught PS 1stb | 0.349 | 0.072 | 0.380 | <0.0005 | 0.125 | ||
| Math anxiety | 0.018 | 0.006 | 0.234 | 0.007 | 0.036 | ||
| Taught PS 1st * math anxiety | −0.028 | 0.012 | −0.184 | 0.019 | 0.026 | ||
| Year | −0.09 | 0.042 | −0.167 | 0.032 | 0.020 | ||
| Math skills | −0.065 | 0.037 | −0.156 | 0.080 | 0.012 | ||
| Reasoning (LCTSR) | 0.012 | 0.011 | 0.103 | 0.261 | 0.002 | ||
| STEM majorc | −0.009 | 0.073 | –0.010 | 0.901 | −0.005 |
Research Questions 3 and 4
If both methods are taught, does the order of instruction affect calculation proficiency? If both methods are taught, does the work type students choose (PS vs. EQ) affect calculation proficiency? Is this effect dependent on student math anxiety? As shown in Figure 2D, student scores on HW calculation items increased after 2 days of instruction compared with 1 day (Figure 2B). However, order of instruction had no effect on performance; independent-samples t test: t(136) = 0.87, d = 0.15, p = 0.39; Mann-Whitney U-test: U = 2651.5, p = 0.21; EQ n = 68, PS n = 70. Next, we used multiple linear regression to target student performance (no. correct) on these post-assessment HW calculation items. Possible predictors included year and STEM major (differed by section); reasoning, math anxiety, and math skills (theoretically predictive of success); treatment order (EQ 1st vs. PS 1st), percent of problems with PS work, and an interaction between percent work PS and math anxiety (experimental questions). Results are shown in Table 4. After both days of instruction, high scientific reasoning ability and STEM major were significant predictors of HW calculation success. Neither instruction order nor work type used was predictive of success, but there was a significant interaction between using PS work and math anxiety (small effect). To better interpret the positive coefficient of this interaction variable, we plotted math anxiety versus raw number of HW problems correct for students who never used PSs and those who always used PSs (Figure 3). By simple linear regression, there was a significant relationship between math anxiety and calculation success for students who never used a PS (m = −0.07, p = 0.0002, R2 = 0.23, n = 55), but there was no significant relationship between anxiety and success when students always used a PS (m = −0.03, p = 0.12, R2 = 0.04, n = 60).
| R2 | Adjusted R2 | Variable | B | SEB | β (standardized) | p value | ω2 a |
|---|---|---|---|---|---|---|---|
| 0.315 | 0.271 | (Intercept) | 0.734 | 0.541 | 0.177 | ||
| Reasoning (LCTSR) | 0.076 | 0.019 | 0.350 | <0.0005 | 0.077 | ||
| STEM majorb | 0.362 | 0.129 | 0.219 | 0.006 | 0.037 | ||
| %PS work*math anxiety | 0.054 | 0.024 | 0.176 | 0.023 | 0.023 | ||
| Math anxiety | −0.019 | 0.012 | −0.140 | 0.114 | 0.008 | ||
| Taught PS 1stc | 0.201 | 0.139 | 0.122 | 0.152 | 0.006 | ||
| Math skills | 0.035 | 0.066 | 0.046 | 0.600 | −0.004 | ||
| Year | 0.034 | 0.075 | 0.035 | 0.653 | −0.004 | ||
| %PS work | −0.043 | 0.154 | −0.024 | 0.781 | −0.005 |
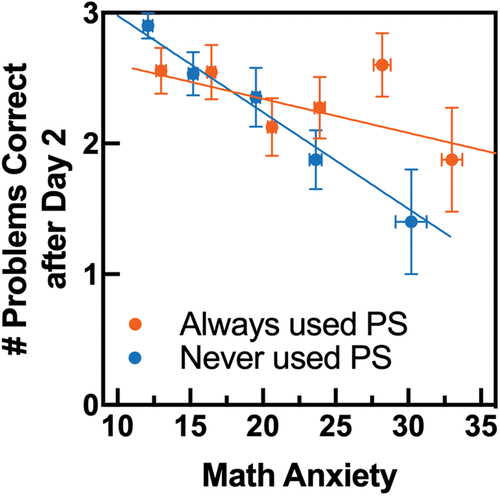
FIGURE 3. Using PSs was helpful for students with high math anxiety. The y-axis represents the number of correct HW calculation problems, with math anxiety scores on the x-axis. For summarizing data, students were grouped by math anxiety by fours (scores 10–13, 14–17, etc.; n = 5–17 students per symbol). Lines represent the best-fit line obtained by simple linear regression using every data point (not the summary points).
Students’ feelings of self-efficacy in their ability to solve HW problems did increase compared with 1 day of instruction for both sections, but comparison of the distributions of the two sections’ confidence levels found them to be indistinguishable by the Mann-Whitney U-test (U = 2388.5, p = 0.84, Cohen’s d = 0.03; EQ 1st: M = 3.58, SD = 0.89, n = 67; PS 1st: M = 3.60, SD = 0.82, n = 70).
Research Question 5
If both methods are taught, does the order of instruction affect students’ understanding of HW equilibrium and the derivation of the HW equations? Is this effect dependent on student math anxiety? To assess students’ levels of understanding of the HW equations after learning both methods, we asked students to derive more complex HW equations (p + q + r = 1 and p2 + q2 + r2 + 2pq + 2 pr + 2qr = 1) to model a three-allele, diploid system given allelic frequency variables p, q, and r (Khan et al., 2018). This was something that was not done or discussed in class, and we expected it to be much more difficult than calculating frequencies for populations in HW equilibrium. Again, students were asked to show their work so we could get a glimpse of their thought processes. Students who learned PSs first were more likely to use a 3 × 3 population PS when deriving the equations (Fisher’s exact test, p = 0.016, odds ratio = 2.63, n = 137; Figure 4A).
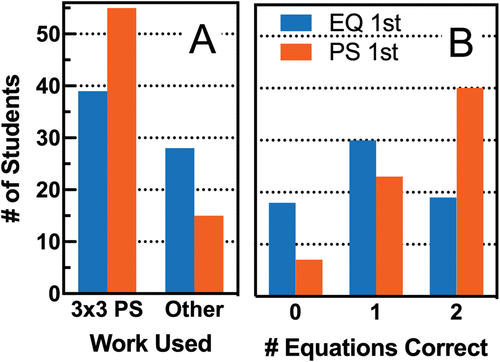
FIGURE 4. Student work deriving more complex HW equations after both days of instruction. Students were asked to derive two HW equations for a three-allele system. (A) The work students showed as they solved this problem was coded as either using a three-by-three PS (3 × 3 PS) or not (Other). Frequency of work used by treatment is shown. (B) Frequency of student performance is shown as number of equations correctly derived (0, 1, or 2).
As shown in Figure 4B, students in the PS 1st section were also more likely to correctly derive the two more complex equations compared with the students in the EQ 1st section (Mann-Whitney U-test: U = 3122.0, p < 0.0005, n = 137). To concurrently consider differences between sections (year and STEM major), student characteristics that would theoretically affect derivation ability (reasoning, math anxiety, math skills), and our experimental questions (treatment order, interaction between treatment order and math anxiety, and use of PSs), we used multiple linear regression to target the number of equations derived correctly. Pre-assessment scientific reasoning (LCTSR) score and treatment order were both significantly predictive of correct derivation of complex HW equations (Table 5). Neither use of a 3 × 3 PS nor an interaction between treatment order and math anxiety were significantly predictive of derivation success.
| R2 | Adjusted R2 | Variable | B | SEB | β (standardized) | p value | ω2 a |
|---|---|---|---|---|---|---|---|
| 0.208 | 0.158 | (Intercept) | −0.055 | 0.533 | 0.918 | ||
| Taught PS 1stb | 0.491 | 0.128 | 0.327 | <0.0005 | 0.086 | ||
| Reasoning (LCTSR) | 0.042 | 0.02 | 0.214 | 0.034 | 0.023 | ||
| Year | 0.105 | 0.073 | 0.119 | 0.152 | 0.007 | ||
| Used 3 × 3 PSc | 0.146 | 0.137 | 0.09 | 0.286 | 0.001 | ||
| Math anxiety | −0.009 | 0.011 | −0.073 | 0.429 | −0.002 | ||
| STEM majord | 0.088 | 0.127 | 0.059 | 0.487 | −0.003 | ||
| Taught PS 1st * math anxiety | 0.006 | 0.02 | 0.026 | 0.753 | −0.006 | ||
| Math skills | 0.01 | 0.064 | 0.015 | 0.877 | −0.006 |
To further assess students’ understanding of HW equilibrium and to specifically investigate their ability to connect math and biology, we asked them to pick an assumption of HW equilibrium and explain why the classic HW equations would not hold if that assumption were violated. As described in the Methods, students’ responses were coded by researchers for multiple characteristics. Unfortunately, our sample size was not large enough to run reliable binomial logistic regression and predict the characteristics of students’ responses with multiple variables at once. Thus, we simply compared the different characteristics of student responses by treatment order and math anxiety using multiple chi-square tests of independence. Because we performed 12 tests (three tests for each of the four variables: one to test the effect of treatment order, and two to test the effect of math anxiety in each section), we used Bonferroni’s correction to set our critical p level for significance, or α, to 0.004. In terms of treatment order and math anxiety, we found no interesting differences in the way students referred to/used PSs or the classic equations and p/q variables in their explanations (unpublished data). Students were also equally likely to correctly integrate math into their explanations regardless of treatment order or math anxiety. As shown in Figure 5A, we did find a close-to-significant association between math anxiety and writing an altered HW equation in the EQ 1st section (blue), with low-anxiety students being more likely to do so; chi-square: χ2(2) = 9.91, p = 0.007, n = 67, φ = 0.38. There was no significant association between anxiety and writing an altered HW equation for the PS 1st section; orange; chi-square: χ2(2) = 1.81, p = 0.40, n = 69, φ = 0.08). Treatment order had no effect on whether or not students attempted to write an altered HW equation in their explanations (Fisher’s exact test, p = 0.67, n = 136).
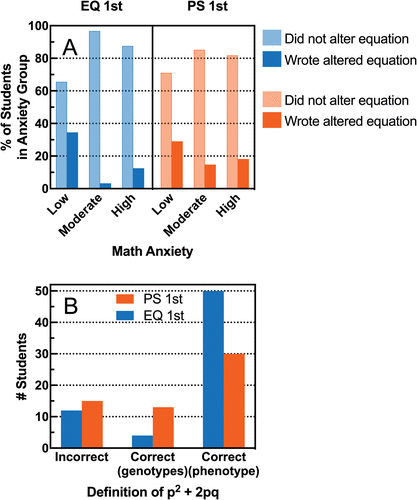
FIGURE 5. Effect of treatment order and math anxiety on student understanding of HW equilibrium. (A) On the post-assessment, students were asked to choose an assumption of HW equilibrium and explain why the classic HW equations would not hold if that assumption were violated. Researchers coded the open responses for whether or not students attempted to create an altered equation. The y-axis shows the percent of students in anxiety groups so that results can easily be compared across groups of differing size (EQ 1st: Low n = 29, Moderate n = 30, High n = 8; PS 1st: Low n = 31, Moderate n = 27, High n = 11). (B) Students were asked to define HW equation terms biologically on the post-assessment, and researchers coded definitions of p2 + 2pq as incorrect, correct but emphasizing the combination of two genotypes, or correct and emphasizing the shared phenotype.
As a final way to investigate students’ understanding of HW equilibrium, we asked students to define each term of the equations using biology vocabulary. No significant differences were found between sections for any of the terms except p2+ 2pq (see Supplemental Table S1). If defining p2+ 2pq as the frequency of either the dominant phenotype or as the sum of the two dominant genotypes (AA and Aa) were both counted as correct, students in the two sections were equally likely to define p2+ 2pq correctly (Fisher’s exact test, p = 0.67; Supplemental Table S1). However, students who learned the PS method first were more likely to define p2+ 2pq as the combination of two genotypes, while students who learned the equations first were more likely to include the overarching idea of the dominant phenotype in their correct definitions; chi-square test: χ2(2) = 6.18, p = 0.045, n = 134, phi = 0.21 (Figure 5C). Because we performed a total of seven tests for definitions, our critical p level for significance, or α, would be 0.007 with Bonferroni’s correction. Thus, this effect would not be considered significant under conservative practices.
Student Instruction Preference and Student Post Anxiety
The majority of students from both sections found the PS instruction more helpful to their learning compared with EQ derivation (Figure 6), but there was no relationship between treatment order and instruction preference (Fisher’s exact test, p = 0.49, n = 133). Additionally, for students who learned the EQ first, there was a relationship between math anxiety and which day of instruction students preferred: students with higher math anxiety were more likely to find the PS instruction day more helpful; χ2(2) = 8.92, p = 0.012, n = 65, phi = 0.37 (Figure 6, blue). For the section that was taught the PS method first, this relationship was not observed, as students at every level of math anxiety preferred the PS instruction; χ2(2) = 0.62, p = 0.73, n = 68, phi = 0.10 (Figure 6, orange).
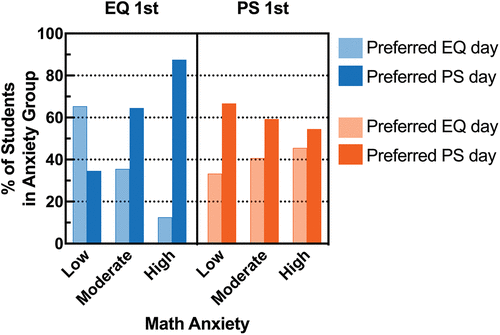
FIGURE 6. In general, students preferred the PS day of instruction, especially for high-anxiety students in the EQ 1st section. On the post-assessment, students were asked which day of instruction was most helpful for their learning. Some students did not follow instructions and circled both options, so these students are excluded from the analysis. The y-axis shows the percent of students in anxiety groups so that results can easily be compared across groups of differing size (EQ 1st: Low n = 26, Moderate n = 31, High n = 8; PS 1st: Low n = 30, Moderate n = 27, High n = 11).
We again assessed math anxiety on the post-assessment to see whether treatment order would affect students’ self-reported math anxiety. We found no difference in math anxiety on the pre- and post-assessments (Supplemental Table S2), no difference between sections, and no interaction between section and time. We should note that the instrument we used to assess math anxiety (Hopko et al., 2003) has questions that ask about how students feel in math-related situations in general (trait-math anxiety) rather than in the moment (state-math anxiety). Thus, we would not necessarily expect our short treatment to change students’ scoring on this instrument.
DISCUSSION
The use of population-level PSs in HW instruction had previously been suggested but not tested (Stencel, 1991; Mertens, 1992; Ortiz et al., 2000). We used a quasi-experimental study design to test the effectiveness of using PSs to teach HW equilibrium and its associated calculations. We were especially interested in the usefulness of population PSs as a calculation aid for students with math anxiety.
Research Question 1
We investigated student performance on HW calculation problems after 2 days of HW instruction (either PS instruction or classic EQ instruction). First, the significance of math anxiety and math skills in the model predicting performance (Table 2) confirmed anecdotal accounts from the literature that both affect performance on HW calculations (Stencel, 1991; Winterer, 2001; Masel, 2012; Brewer and Gardner, 2013). In terms of our treatment, we were interested in how students who were taught to perform HW calculations using a PS as an aid would compare to those who learned the classic EQ. This is important, because we did not want to take quantitative reasoning out of population genetics. Rather, our goal was to be creative about the way we taught students to use mathematical models in hopes of leveling the playing field for those with math anxiety. We found that PS instruction did not disadvantage students in terms of calculation proficiency. If anything, PS instruction may have led to increased HW calculation performance (Figure 2B and Table 2), but, if real, the effect was small (ω2 = 0.014, B = 0.3 questions).
Performance on the first question of the mid-assessment seemed to be affected by PS instruction the most. One difference between question 1 and the other two questions is that the given frequency was not explicitly named. Rather, students had to read “20% of the US population cannot taste PTC” and realize that a phenotypic frequency was given. In the other two questions, “the frequency of the recessive allele” and “95% of a population has the normal phenotype” aligned more closely with the exact definitions that were given of the equation variables. Thus, it appears that learning to approach question 1 using a PS may have helped students avoid mistaking the frequency of the inability to taste PTC (a phenotype) as an allelic frequency (the most common mistake).
This could suggest that the PS, a model that may have already had biological meaning for the students after learning about inheritance, helped students keep track of the different types of biological entities (alleles vs. genotypes vs. phenotypes) better than the foreign symbols p and q (which previously had no meaning for students), especially when biological entities were not explicitly named. However, research suggests that many students do not understand the science behind PSs even though they are familiar with the tool. Tolman (1982) reported that 80% of students in the study commonly assigned the wrong number of alleles to parents and offspring while using a PS, demonstrating that the biological concepts tied to the PS were not clearly understood. Other studies have shown that when solving monohybrid and dihybrid cross problems, students can get the right answer using a PS without being able to explain the processes they are representing (Stewart, 1982, 1983; Moll and Allen, 1987). Thus, students are often filling out a PS as a learned algorithm when solving genetics problems rather than understanding the biological concepts of meiosis, genetic combination, and inheritance (Moll and Allen, 1987; Stewart and Kirk, 1990). To ensure better understanding of the impact of PS instruction on students’ ability to correctly identify different biological entities, future research should use an assessment that contains a greater number of HW calculation problems that are carefully varied to provide and ask for different biological entities with different wording. Follow-up interviews would also be useful to investigate the specific ways students are using PSs and whether an approach is more algorithmic, biology focused, or a combination of the two.
We had originally hypothesized that PS instruction would benefit students with higher math anxiety more than their low-anxiety peers. We thought that the visual PS tool would not trigger math anxiety in the same way as an equation would with its symbols, thus not using up working memory. However, we did not see a significant interaction between treatment (EQ vs. PS) and math anxiety (Table 2). Perhaps an assessment immediately after that first day of instruction was not sufficient to show any differential benefits for high- versus low-anxiety students. It is also possible that PS instruction benefits students with all math anxiety levels.
Benefits of PSs even for low-anxiety students could be explained by cognitive load theory. Intrinsic cognitive load is considered inherent for a given task, dependent on the necessary interactivity of all of its component parts, and unchangeable, except by altering the knowledge of the learner; however, extraneous cognitive load can be altered, as it is caused by the unnecessary information processing imposed by our instructional strategies (Sweller, 2010; Sweller et al., 1998, 2019). The element interactivity, and thus the intrinsic cognitive load, of the concept of HW equilibrium is high by nature, because students must understand the connected concepts of alleles, genotypes, phenotypes, gametes, inheritance, and the assumptions of equilibrium plus the interdependent quantitative relationships between biological entities. Normally, the abstract p and q symbols are another element that students must use to connect the biology and math. Using a PS as a calculation aid (and later a scaffold for deriving the equations) could reduce extraneous load, because it eliminates (or delays) the need for those abstract symbols, allowing the biological concepts to be directly connected to their quantitative relationships without an intermediate. In addition to unneeded element interactivity, split attention has long been postulated to increase extraneous cognitive load (Chandler and Sweller, 1992; Sweller et al., 1998), and a large meta-analysis confirmed that integrating instructional materials spatially results in learning gains (Ginns, 2006). Thus, the population PS may also reduce extraneous cognitive load by visually integrating the biological concepts (alleles, genotypes, gametes, inheritance) and the actual mathematical calculations. However, as discussed earlier, lessening extraneous cognitive load by using PSs as an algorithmic tool would not necessarily mean that students have a better understanding of the biology.
Research Question 2
As we investigated the work type students chose to use after learning both methods, our first finding was that students tended to stick with the first method they were taught (Figure 2C and Table 3). This is similar to established findings in mathematics education that teaching computational procedures first interferes with subsequent conceptual development, in that students tend to stay focused on the procedures (Kamii and Dominick, 1998; Kieran, 1984; Mack, 1990; Pesek and Kirshner, 2000). However, our study adds a different dimension, in that this was not only true of procedural knowledge, but that students tended to prefer whatever method it was that they learned first.
Second, we saw an interaction between math anxiety and treatment order in terms of work type used (Figure 2C and Table 3). Why would math anxiety influence work type choice in the EQ 1st section differently than in the PS 1st section? This would make sense if students’ math anxiety was triggered more in the EQ 1st section. Past work in neurobiology has found that simply viewing mathematical equations can trigger a neural response related to threat avoidance in individuals with high levels of math anxiety (Pizzie and Kraemer, 2017). Even without a stimulus, cortical network structure differences between low– and high–math anxiety individuals are apparent as subjects simply anticipate performing math (Klados et al., 2017). During day 1 of instruction, students in the EQ 1st section saw equations and thus may have been stimulated to anticipate math, while PS 1st students never saw an equation or a stimulus to warn them that math was coming. Thus, we would expect students with math anxiety to have that anxiety triggered more in the EQ 1st section than the PS 1st section. Students in the PS 1st section did see and use equations on day 2, but it is possible that seeing the equations on day 2 did not elicit the same level of math anxiety as it would have on day 1, because the students had already been performing the calculations; the equations already had meaning beyond just being a math equation. This would be better supported in our data if we had seen moderate- or high-anxiety students in the PS 1st group abandoning the PS method to use the EQ after day 2, but we did not even see many low-anxiety students do this (compare Figure 2A and C, orange). Rather, it was the moderate- and high-anxiety students in the EQ 1st section abandoning the EQ for the PS method (Figure 2A and C, blue). Thus, it seems plausible that math anxiety was invoked in the EQ 1st section, leading moderate- and high-anxiety students to adopt the visual PS method, but we cannot say for sure whether moderate- and high-anxiety students in the PS section had that same anxiety triggered or not. In the future, we could explicitly test this hypothesis by repeating this study with a method for assessing state-math anxiety (in specific moments and in connection with specific tasks) as opposed to trait-math anxiety (Orbach et al., 2019).
We should also note that some students were more flexible in their use of the visual PS method than others. In coding student work, we included anything that resembled a PS, but students differed in how they drew them in some cases (e.g., different-sized boxes vs. uniform sizes despite different allelic frequencies, outermost border of the box present vs. absent, etc.). This could be related to more algorithmic thinking (as discussed earlier) rather than using the PS as a true biological model. Future qualitative work will be helpful to understand why students draw PSs the way that they do and how that influences their thinking about the mathematical task.
Research Questions 3 and 4
Although all students ended up learning both methods (EQ and PS), we were interested in whether the order of instruction and the work type students chose would impact their calculation proficiency. Instruction order did not significantly predict HW calculation performance after day 2 of instruction (Figure 2D and Table 4). Thus, while students had been taught both methods, the order in which they were taught did not appear to directly impact student performance. However, treatment order may impact scores indirectly due to effects of work type used, as students in the PS 1st section were more likely to use a PS (Table 3). While using a PS was not significantly predictive of scores on its own, there was a positive interaction between using PSs and math anxiety (Table 4, small effect). As shown visually in Figure 3, using PS work specifically helped students with high math anxiety.
Perhaps for high-anxiety students, avoiding the equations reduces the effect of their math anxiety and frees up working memory for performing the calculations (Ashcraft and Kirk, 2001). As discussed earlier, using a PS to perform the calculations also may have reduced extraneous load via the split-attention effect (Chandler and Sweller, 1992) or by reducing element connectivity (Sweller, 2010), as high-anxiety students could use the PS to avoid the abstract p and q variables. Using a PS did not seem to benefit low-anxiety students (Figure 3), perhaps because they are already performing near the ceiling of what our assessment could detect. It is also feasible that the PS method actually starts to increase extraneous load for low-anxiety students because they have obtained more expertise (termed “the expertise reversal effect”; Chen et al., 2017) or because the PS is now redundant for them (termed “the redundancy effect”; Chandler and Sweller, 1991). However, if the PS method truly increases extraneous load for low-anxiety students, they would likely just refrain from using the PS and use the equations instead to reduce their mental effort. It is also possible that low-anxiety students were framing the problem as a PS in their mind even when not physically drawing it. Leutner et al. (2009) found that imagining images reduced cognitive load and increased comprehension, but our methods did not allow for us to know whether or not students imagined the visual image they had been taught unless they drew it. Again, future qualitative interviews would allow for a better understanding of why students choose to use PSs, and studies with actual cognitive load assessments would be helpful.
Research Question 5
Overall, we have somewhat conflicting evidence regarding whether teaching the PS or EQ first leads to greater student understanding of HW equilibrium. First, we looked at students’ ability to derive more complex HW equations that had never been discussed in class. As shown in Figure 4A, students who were taught PSs first were more likely to use a 3 × 3 PS. This was interesting, because both sections had learned the connection between the equations and the population PS, but only the PS 1st section had connected the PS and EQ together when deriving the EQ for the first time (on day 2). The EQ 1st section derived the equations on day 1 before being introduced to a PS. The method they used to derive the equation the first time clearly mattered. Again, like computation procedures interfering with later conceptual understanding (Kieran, 1984; Mack, 1990; Kamii and Dominick, 1998; Pesek and Kirshner, 2000), the context in which they first derived the equations seemed to be more memorable for them than later connections. While the PS 1st section was more likely to use a PS when solving this problem (Figure 4A), the type of work used did not have a significant effect on performance on this problem (Table 5).
Treatment order did significantly predict success: students who learned the PS method first were more likely to correctly derive the two more complex HW equations for a three-allele system (Figure 4B and Table 5). Learning the PS method first predicted that students would derive an additional 0.5 of an equation correctly (see coefficients of Table 5), a large effect in practical terms but close to medium in terms of variation explained (ω2 = 0.09). These data support the hypothesis that learning HW equilibrium using a PS before the equations are introduced increases students’ understanding of the equations themselves.
As with any study in which two instructional methods are compared, it is possible that one treatment led to more learning because it was just a better lesson overall (more student-centered, more active, etc.). We believe that is unlikely here. In both sections, students were asked to work in pairs or groups to generate equation terms and the mathematical relationships between terms on their own before the equations were derived as a class on the board. The instructor used students’ ideas for this derivation on the board, so the instruction for both sections emphasized student-generated equations. The only differences we can think of (other than the timing in relation to PS instruction) is whether summing equation terms to 1 was discussed before or after term generation and whether specific allelic frequencies were part of the derivation discussion. Students in the EQ 1st section first came up with all of the terms and then were prompted to notice their mathematical relationship (that they all summed to 1), because they started with specific allelic frequencies (p = 0.7, q = 0.3) in addition to generalizable terms (p and q). On the other hand, students in the PS 1st section were told that their terms should sum to 1 before terms were generated (because summing to 1 had already been part of solving problems with the PS), and they were not given specific allelic frequencies to use during their derivation. The post-assessment question asked the students to derive the equations in terms of p, q, and r (no specific allelic frequencies were given), so it was slightly more similar to the PS 1st students’ experience. However, the EQ 1st students also derived the equations with p and q, so the post-assessment prompt was still similar to the activity they did in class.
The bigger difference between sections was that students in the EQ 1st section were introduced to the principles of population genetics and the probability of generating offspring with different genotypes at the same time as they were deriving the EQ with its abstract symbols. On the other hand, students in the PS 1st section had already been introduced to the principles of population genetics and the probability of generating different offspring using the PS and had been performing the calculations before the abstract symbols of the EQ were introduced. By the time they reached EQ derivation on day 2, students in the PS 1st section may have already formed schemas about HW equilibrium (even the quantitative concepts), freeing up working memory to understand the meaning behind the abstract symbols and equations when they first came in contact with them. Even if these students used the PS as an algorithmic tool rather than completely understanding the biology behind it, as is often the case, this may still have reduced the cognitive load of EQ derivation.
We also investigated students’ understanding of HW equilibrium using an open-response question about violating an assumption of HW equilibrium and by asking students to define the HW EQ terms. We generally did not see differences by treatment order in answers about HW assumption violations. However, in Figure 5A, we see whether students generated an altered equation in their response (a mathematical task that demonstrates an explicit connection between the assumptions of HW equilibrium and the HW EQ). The data of Figure 5A could be evidence that math anxiety was not triggered as much in the PS 1st section (orange), as math anxiety was not predictive of students’ tendency to generate a novel equation like it was in the EQ 1st section (blue). Future research with state-based measurements of math anxiety would be needed to verify this conclusion.
On the other hand, the results of Figure 5B suggest that learning the EQ first may possibly help students focus on the big picture of phenotypes. We had originally expected the opposite trend, supposing that the PS method would help students see the holistic biological picture of phenotype rather than separate terms of an equation. The greater likelihood of EQ 1st students to see the big picture is especially surprising, because students in the EQ 1st section were more likely to misinterpret a given dominant phenotype on the first question of the mid-assessment. We also cannot ignore the possibility that EQ 1st students were simply more likely to memorize the given definition of p2+ 2pq (“frequency of the dominant phenotype”) that was written on a review slide shown during day 1 of instruction. More rigorous qualitative data would be needed to determine whether the EQ 1st treatment truly led to greater mastery of the meaning of p2+ 2pq.
Limitations
As discussed in the Methods, our sample size (n = 141) was limited to students who would consent, which limits our statistical power. A priori power analyses suggested that we had sufficient power to detect medium or large effect sizes, but not small effects. Our effects that were medium sized or approaching medium sized (and thus those we are the most confident about) are 1) the effect of treatment order on the work type students chose (Table 3), 2) the effect of treatment order on the ability to derive more complex HW equations (Table 5), 3) the relationship between math anxiety and attempting to create an altered HW equation for a violated assumption in the EQ 1st section (Figure 5A), and 4) the association between math anxiety and instruction preference in the EQ 1st section (Figure 6).
We saw the following small effects: 1) treatment on calculation performance after 1 day (Table 2), 2) treatment order interacting with math anxiety to predict work type used after 2 days (Table 3), 3) PS work interacting with math anxiety to predict calculation success after 2 days (Table 4), and 4) the association between treatment order and defining p2+ 2pq as a phenotype (Figure 5B). Thus, like other educational studies conducted in small- or medium-enrollment courses, our low-power, small effects should be interpreted cautiously, and the exact effect sizes may be exaggerated here. There also may be other small effects that we were not able to detect. Future studies in larger-enrollment courses would be useful to confirm these results.
Our work is also limited in that we only assessed pre and post math anxiety as a trait rather than looking at state measurements of anxiety. We can also only hypothesize about the effect of PS versus EQ on students’ cognitive load. In future research, it would be interesting to repeat this experiment with sophisticated methods for assessing in-the-moment math anxiety and cognitive load and include qualitative data about student thought processes.
Implications for Instructors
We suggest the following implications for instructors. If time permits only one method to be taught, we recommend teaching the population-level PS method. This method still allows for students to learn the same mathematical relationships of HW equilibrium without sacrificing calculation proficiency (see Figure 2B and Table 2). This method may even slightly increase student success in HW calculations compared with teaching students to derive and use the equations, possibly due to a decrease in extraneous cognitive load usually imposed by the abstract equations. This choice is further supported by our attitudinal data. When asked to pick which day of instruction was most helpful in our study, a majority of moderate- and high-anxiety students in both sections chose the PS day (Figure 6). Low-math anxiety students in the EQ 1st section did generally prefer the EQ day, but low-anxiety students in the PS 1st section preferred the PS day. Using only the PS method still allows students to perform all of the same calculations that they normally would when using the classic HW equations, but they will not be familiar with the conventional p and q variables. This would not matter in a nonmajors’ course, but it is worth considering for majors based on needs in more advanced courses.
Overall, students appear to benefit from learning both methods over 2 days of HW equilibrium instruction. In our study, student scores on HW calculation items improved after 2 days of instruction (compare Figure 2B and D), and giving 2 days of instruction leveled the playing field somewhat for students with high math anxiety and low math skills (compare the effect of these two variables in Tables 2 and 4). We should also note that these 2 days of instruction only covered the general principle of HW equilibrium, calculating allelic frequencies from observed genotypic frequencies, and calculating predicted allelic, genotypic, or phenotypic frequencies for populations in HW equilibrium. Instructors may want to add more instructional days to cover other extensions of these topics.
If instructors choose to include two class sessions on HW equilibrium and teach both methods, students appear to benefit from learning the population PS method first, especially students with high levels of math anxiety. Learning to use PSs as a calculation aid before equations are introduced may be less likely to trigger math anxiety (see Figures 2C, 5A, and 6, and Table 3 for examples of math anxiety being predictive of student choices only in the EQ 1st section). In our study, teaching the PS method first also made it more likely that students would use a PS when solving problems (Figures 2C and 4A, and Table 3), and using PS work may help high–math anxiety students be more successful when performing HW calculations (Figure 3 and Table 4). Learning to perform calculations using a population PS before deriving the HW equations also appears to increase student ability to derive more complex equations on their own (Figure 4B and Table 5), suggesting that the equation derivation done together in class had more meaning to them after they already had experience with the mathematical relationships using the PS as a tool. Our study makes it less clear whether treatment order matters for overall student understanding of the biological concept of HW equilibrium (Figure 5) and whether the PS is providing students with greater biological understanding of the inheritance process or just a helpful algorithm.
Other instructional methods for HW equilibrium exist, notably simulating populations in HW equilibrium (Winterer, 2001; Brewer and Gardner, 2013;) and enlisting the aid of computers to sidestep calculations (Mariner, 1973; Carlton et al., 2004). These also may prove to be valuable activities for generating student understanding of this difficult concept, and the effects of these methods and the interactions between various methods remain unresolved. Future research is needed to determine the generalizability of our results to other populations (biology majors, students with different levels of math preparedness and math anxiety, other institutions, etc.) and other quantitative topics in biology where equation derivation is relevant.
ACKNOWLEDGMENTS
The authors would like to acknowledge Ashley Hale for design work on Figure 1 and Brinley Zabriskie for consultation about our statistical methods.