Learning Introductory Biology: Students’ Concept-Building Approaches Predict Transfer on Biology Exams
Abstract
Previous studies have found that students’ concept-building approaches, identified a priori with a cognitive psychology laboratory task, are associated with student exam performances in chemistry classes. Abstraction learners (those who extract the principles underlying related examples) performed better than exemplar learners (those who focus on memorizing the training exemplars and responses) on transfer exam questions but not retention questions, after accounting for general ability. We extended these findings to introductory biology courses in which active-learning techniques were used to try to foster deep conceptual learning. Exams were constructed to contain both transfer and retention questions. Abstraction learners demonstrated better performance than exemplar learners on the transfer questions but not on the retention questions. These results were not moderated by indices of crystallized or fluid intelligence. Our central interpretation is that students identified as abstraction learners appear to construct a deep understanding of the concepts (presumably based on abstract underpinnings), thereby enabling them to apply and generalize the concepts to scenarios and instantiations not seen during instruction (transfer questions). By contrast, other students appear to base their representations on memorized instructed examples, leading to good performance on retention questions but not transfer questions.
LEARNING INTRODUCTORY BIOLOGY: STUDENTS’ CONCEPT-BUILDING APPROACHES PREDICT TRANSFER ON BIOLOGY EXAMS
A central goal in college biology courses is for students to gain conceptual understanding of core concepts, rather than committing to memory a large corpus of biology facts (e.g., National Research Council [NRC], 1996; Jensen et al., 2014). This type of deep conceptual understanding is best assessed by performance on questions that require students to apply learned concepts to new contexts and situations (Anderson et al., 2001), also known as transfer questions (Loibl et al., 2017). Although many biology courses primarily focus on comprehension and understanding (Momsen et al., 2010), some ambitious instructors exclusively assess students with higher-order questions (such as application, analysis, synthesis, and evaluation) that are designed to assess and reinforce acquisition of deep conceptual understanding (e.g., see Bissell and Lemons, 2006; Crowe et al., 2008; Jensen et al., 2020). Another type of question to assess deep conceptual understanding is a transfer question; these questions require the students to solve problems that go beyond previously taught or worked examples (Barnett and Ceci, 2002; for examples in general chemistry, see McDaniel et al., 2018; Frey et al., 2020). In the present study, we focus on transfer questions as the higher-order assessment.
To support these educational goals, for at least two decades (e.g., see National Science Education Standards; NRC, 1996), science educators have suggested incorporating an active-learning approach into science instruction, and college biology pedagogy has tended to embrace this approach (e.g., Knight and Wood, 2005; Armstrong et al., 2007; Haak et al., 2011; Luckie et al., 2012; Auerbach et al., 2018; Halmo et al., 2020; Jensen et al., 2020). A recent meta-analysis supports this stance. Based on approximately 310 studies in peer-reviewed journals (from biology, chemistry, engineering, or physics courses), Freeman et al. (2014) reported generally higher postcourse performance on exams and concept inventories for courses that included active-learning (interactive engagement) instruction versus courses that relied extensively on traditional instructional methods (e.g., lecture). Given this overwhelming evidence for the benefits of incorporating active learning into science instruction, Freeman and colleagues (2014, p. 8413) suggested that a productive focus for “second-generation research” would be to use advances in educational psychology and cognitive science to test hypotheses about which type of active learning is most appropriate and efficient for certain student populations.
The present study responds to this call for a next-generation focus on how students achieve conceptual understanding in active-learning classrooms. We appeal to current findings in cognitive science (e.g., McDaniel et al., 2014; Little and McDaniel, 2015) and chemistry education (Frey et al., 2017, 2020; McDaniel et al., 2018) to advance novel hypotheses about the influence of individual differences in concept-building approaches (described in the following section) on students’ success in applying content knowledge learned in their introductory biology courses (courses incorporating active-learning techniques). We first outline the theoretical framework, review initial findings that support the framework in chemistry education, and then introduce the current study.
Individual Differences in Concept-Building Tendencies
Our theoretical orientation is based on basic research in cognitive science demonstrating that, for a given conceptual learning challenge, individual learners can extract qualitatively different representations. That basic work has revealed two fundamental types of representations. One type is primarily based on memorizing the individual training examples, termed “exemplar based” (Medin and Schaffer, 1978; Nosofsky, 1984; Kruschke, 1992). The other type is based on the abstract regularities (e.g., rules) that capture the relations among the training examples, termed “abstractor based” (Bourne, 1974; Little et al., 2011). The literature has established that some learners construct exemplar representations (termed “exemplar learners”), whereas other learners extract an underlying abstraction of the training set (termed “abstraction learners”) for a range of laboratory conceptual learning tasks, including category learning (e.g., Craig and Lewandowsky, 2012; Little and McDaniel, 2015), function learning (McDaniel et al., 2014), multiple-cue prediction learning (Juslin et al., 2003; Hoffmann et al., 2014), and skill learning (Bourne et al., 2010).
A key theoretical foundation of the present study is that a learner’s tendency toward an exemplar-based versus abstractor-based approach to conceptual learning can be relatively stable across very different kinds of conceptual-learning tasks (McDaniel et al., 2014; see later discussion regarding the stability of concept-building approaches across time). Support for this assumption comes from a study in which learners completed a laboratory function-learning task followed by unrelated categorization tasks over the following several weeks (McDaniel et al., 2014). From their pattern of extrapolation performance in the function-learning task, learners were identified as adopting an approach of memorizing the particular training pairs (each input value–output value pair) or an approach of abstracting the function rule (a bilinear “V shape”). The crucial result was that learners’ approaches on the function-learning task predicted their performances on two unrelated categorization tasks. Those who appeared to memorize particular training pairs on the function-learning task (i.e., exemplar learners) demonstrated categorization performance that reflected an exemplar representation (on the categorization transfer tests), whereas those learners who displayed rule learning on the function-learning task (abstraction learners) showed abstraction-driven categorization performance (on the categorization transfer tests). Further, students’ tendency to rely on exemplar- versus abstractor-based concept-learning approaches was only modestly associated with their working memory capacity and with their fluid intelligence; together, working memory and fluid intelligence accounted for 10.4% of the variance in learner type (McDaniel et al., 2014).
Especially critical for the present focus on science, technology, engineering, and mathematics (STEM) learning, several recent studies have converged on the conclusion that these individual differences in conceptual representations revealed on laboratory learning tasks appear to extend to students’ learning of chemistry (Frey et al., 2017, 2020; McDaniel et al., 2018). First, students in chemistry classes who displayed exemplar-learning tendencies (as determined by a laboratory learning instrument described in Methods) performed less well on summative assessments (exams) in the first two semesters of general chemistry and in organic chemistry II (Frey et al., 2017). Indeed, organic chemistry, the course that arguably required the most abstraction for successful exam performance, showed the most prominent performance decrements for students with an exemplar-based concept-building tendency relative to those with an abstraction-based concept-building tendency. Second, for the exams given in the first semester of general chemistry, the exam items (problems) were subsequently classified as requiring generalization and transfer of content from class lectures and homework (transfer items) or as requiring responses based directly on previously-trained problems (retention items). When students’ performances were re-examined separately for transfer and retention items, a more nuanced pattern emerged (McDaniel et al., 2018). Exemplar learners performed relatively poorly relative to the abstraction learners on transfer exam items (problems), but those same learners performed equivalently to abstraction learners on retention exam items.
In a more recent study, a small sample of students was asked to think aloud while solving several problems related to their general chemistry instruction, one problem representing a retention problem and two other problems requiring transfer (Frey et al., 2020, study 2). Those students with an exemplar concept-building tendency often relied on algorithms associated with a particular example problem and its solution presented in class or homework without understanding the principles behind the algorithms. By contrast, students who displayed tendencies to abstract in the laboratory learning task tended to rely on the principles and concepts that were the underpinnings of the class or homework problems. Further, the exemplar learners showed a sharp decline in performance accuracy on the transfer problems (especially far transfer) relative to the retention problem, whereas the performance decline for the abstraction learners was not as severe (because of the small N, these observations could not be confirmed with formal statistical tests). Overall, then, at least in several general chemistry courses, the reported patterns are consistent with the idea that those students with exemplar-based concept-building tendencies constructed representations that were rich in the surface features of studied problems (i.e., memorized examples; cf. Regehr and Brooks, 1993), thereby disfavoring transfer to novel problems (Gick and Holyoak, 1980; Novick, 1988) but not penalizing performance on problems (exam items) that were very similar to studied problems (e.g., Novick, 1988). In contrast, those with abstraction concept-building tendencies constructed representations of studied problems that captured deep-structure characteristics of problems (abstract characteristics), thereby supporting transfer (Gick and Holyoak, 1983).
Overview of the Current Study
In this study, we examined the idea that the influence of students’ concept-building tendencies extends to learning in introductory biology. Overlap exists between undergraduate chemistry and biology in terms of the students who take the courses, concepts, and problem types, yet the two differ in important ways. Chemistry demands that students solve problems using quantitative reasoning, visual pattern recognition, and heuristics. Biology demands that students develop an extensive vocabulary, knowledge of processes, and analysis of patterns from graphs and tables. Although quantitative reasoning is essential to biology as a discipline, many undergraduate biology courses do not emphasize quantitative problem solving. Biology problems in this study involved recall and understanding of terms and concepts, but the transfer problems involved reasoning from information and data (e.g., as presented in tables and graphs) and linking inferences to conceptual understanding of biological processes. This study enabled us to extend prior work by focusing on retention and transfer questions for nonquantitative problem solving that involves reasoning and inference (for a related case-study in general chemistry, see Frey et al., 2020).
To achieve this aim, we adopted and refined the approach reported in McDaniel et al. (2018). One potential limitation of this approach is that examination items were classified as retention or transfer items after the examination was administered. In the present study, we constructed retention and transfer examination items a priori by considering the content and activities students completed in class and as homework (these item types are fully described in Methods). Based on the prior theoretical work and classroom research summarized earlier, we posited that some learners would tend to rely on exemplar learning (e.g., memorization) to support their acquisition of biology content (learners with exemplar-learning concept-building tendencies, as determined by our laboratory learning instrument), and other learners would tend to rely on abstraction (deeper understanding) of the underlying principles and concepts of biology (learners with abstraction-based concept-building tendencies). Based on this hypothesis, we predicted the following patterns of exam performance. For the retention exam items, the exemplar learners would fare relatively well, performing at levels comparable to those displayed by abstraction learners. In contrast, on the transfer items—the exam items that required extension or application of the underlying principles—the exemplar learners would show significant declines in performance relative to the abstraction learners.
We emphasize that these predictions assume a strong influence of students’ concept-building approaches in terms of the nature of the representations they construct for the instructed biology content. It is important to reiterate that the present study was conducted in biology courses incorporating an array of active-learning techniques. The instructors framed their courses around real-world problems to increase student interest. They used inclusive strategies, such as learning students’ names and emphasizing that all students could be successful. During class time, the instructors frequently interrupted lecture, which focused on key concepts and scientific practices, to pose questions that students answered via note cards or response systems. Students worked in informal groups, and the instructors led students in small- and large-group discussion. They addressed students’ questions responsively, based on the common challenges emerging during class (the Appendix in the Supplemental Material provides a description of one lesson). Courses designed with active-learning pedagogy are intended to focus students on understanding the underlying principles, concepts, and abstractions that are core to the biology curriculum, rather than emphasizing memorization of the examples and facts that illuminate underlying principles and concepts (Knight and Wood, 2005; Haak et al., 2011; Auerbach et al., 2018; Halmo et al., 2020; Jensen et al., 2020). The theoretical orientation (and supporting empirical work) guiding the present study suggests, however, that there is a subset of students (who can be identified a priori) with the exemplar concept-building approach (i.e., a reliance on memory of examples to represent the content) that might override the intended thrust of active-learning techniques, at least the techniques adopted in the introductory biology courses examined herein.
One final feature of this study warrants mention. An alternative interpretation that might be offered for the predicted patterns is that the anticipated advantage on transfer items (on the exams) for students with abstraction concept-building approaches is wholly a consequence of individual differences in general ability or intelligence (e.g., Putz-Osterloh, 1981; Putz-Osterloh and Luer, 1981; Wenke et al., 2005). That is, students with abstraction concept-building approaches tend to have modestly higher levels of fluid intelligence than students with exemplar-learning tendencies (McDaniel et al., 2014; but see Little and McDaniel, 2015, for a counter finding), and these differential levels of intelligence might be responsible for the superior performance on transfer items anticipated for the abstraction learners. Though previous studies have found that concept-building tendencies are not highly related to general ability or intelligence, and moreover, that general ability or intelligence does not account for the relation between concept-building approaches and transfer (Frey et al., 2017; McDaniel et al., 2014, 2018), we nevertheless thought it prudent to continue to explore this possible alternative interpretation for learning and transfer of biology content. We used students’ composite ACT scores (includes math, English, and, reading) or concordant Scholastic Aptitude Test (SAT) scores (Dorans, 1999) as an index of general ability (also termed crystallized intelligence). We administered the Raven’s Advanced Progressive Matrices (RAPM; Raven et al., 1991) to index fluid intelligence; the RAPM is a psychometrically sound measure commonly used to assess fluid intelligence (e.g., Jonsson et al., 2021). To determine whether the patterns of results associated with concept-building tendency might be more directly a consequence of general ability, fluid intelligence, or both, we included SAT/ACT and RAPM scores as covariates in our analyses. If concept-building approaches reflect cognitive mechanisms above and beyond general ability and intelligence, then significant advantages of abstraction learners for transfer items should emerge even after accounting for general intelligence.
METHODS
Study Design
The major factor in the design was the designation of students as exemplar learners or abstractor learners, based on their performances on an unrelated (to the course content) laboratory function–learning task (described in detail in a following section). Because the function-learning task is computer paced and requires approximately 40–60 minutes to complete, students had to do the task outside class and online. The task is challenging, and with online administration, past studies indicate that a significant proportion of students either do not complete the task or fail to meet the learning criterion (Frey et al., 2017; McDaniel et al., 2018; when learning is incomplete, extrapolation performances are ambiguous with regard to the learners’ emerging representations). In line with this, the current study focused primarily on the 67 students who met the function-learning task criterion (21 exemplar learners; 46 abstractor learners), representing 43% of the students from the introductory biology classes who participated.
The outcome variable of interest was midterm exam performances as a function of exam question type. Each of four midterms was constructed to include questions that reflected retention of taught content and questions that required transfer of taught content (this distinction is detailed in a following section). Thus, the study reflected a 2 × 2 mixed factorial design with learning approach (exemplar vs. abstraction learner) as the between-subjects factor and exam question type (retention, transfer) as the within-subjects factor.
Context and Participants
The UGA institutional review board approved this study under exempt status (STUDY00000660 and PROJECT000000090). Data collection for the study took place during Spring and Summer semesters of 2018 at a research-intensive institution in the southeastern United States. Spring 2018 participants were enrolled in one section of the first-semester introductory biology course offered at this university (BIOL 1107). The course was taught by one instructor and focused on cells and cell division, biomolecular structure and function, cell transport and signal transduction, patterns of inheritance, and basic carbohydrate metabolism. Summer 2018 participants were enrolled in one section of the second-semester introductory biology course offered at this university (BIOL 1108). The course was taught by a different instructor and focused on micro- and macroevolutionary mechanisms, speciation and phylogenetics, homeostasis and physiology, ecological species interactions, and ecosystem dynamics. In both semesters, all enrolled students (first-semester course: N = 142; second-semester course: N = 77) were invited to participate and to complete study activities as a normal part of their course work. Students who participated received a small amount of course credit for their participation (approximately 1% or less of overall points in the course).
Table 1 summarizes the points of exclusion and the number of students excluded at each step to arrive at the final samples. For the final samples, it also identifies the number of abstraction learners, exemplar learners, and non-learners (those excluded for having a final training block the mean absolute error [MAE] ≥10, as described in a following section). Twenty-three of the 133 consenters in the first-semester course were excluded from the concept-building sample: six did not complete all exams, and 17 others did not complete the concept-building task. In the second-semester course, 30 of the 75 consenters were excluded from the concept-building sample: six were repeat students from the first-semester sample, two did not complete all exams, and 22 did not complete the concept-building task. In the next step, for analysis involving ACT as a single covariate, four students in the first semester and three students in the second semester were removed from the concept-building sample for not having ACT or SAT scores available from the registrar (SAT scores were converted to ACT equivalent scores; Dorans, 1999). Finally, for analysis involving both ACT and RAPM as covariates, 12 students from the first semester and six students from the second semester were removed from the ACT sample for not completing the RAPM task. Table 1 contains information about the sample for each analysis.
| BIOL 1107 | BIOL 1108 | Total | |
| Total students | 142 | 77 | 219 |
| Consenters | 133 | 75 | 208 |
| Concept-building sample | 110
| 45
| 155
|
| ACT sample | 106
| 42
| 148
|
| RAPM sample | 100
| 30
| 130
|
Data Collection
Development of Exam Questions.
To ensure that exams for both the first- and second-semester courses contained both retention and transfer items, the course instructors (one of whom was author L.B.L.) worked together with author P.P.L. as follows: First, the course instructors created exam questions aligned with the course learning objectives for each exam. Instructors aimed to create at least five transfer items per exam. After doing so, each instructor made a preliminary rating of every exam item according to four categories specified in the McDaniel et al. (2018) rubric: category 1 indicated questions very similar to how the material was covered in class or homework (retention items); category 2 indicated covered material, but the question required applying it to a new situation (i.e., a comparison); category 3 indicated using learned material to address a situation/problem that could appear foreign or different from all previous presentations; and category 4 indicated problems that required the highest level of thinking and application, often conceptual thinking beyond the scope of algorithms or focused lecture topics (McDaniel et al., 2018, p. 243). Following McDaniel et al., category 1 items were considered retention items and category 3 or 4 items were considered transfer items; category 2 items did not seem to fall definitively within the retention or transfer categories and thus were not included in the present analyses (as in McDaniel et al., 2018).
After the exam draft was created, P.P.L., who had previously taught the material for both courses, reviewed the exams and independently rated each item. She sent her rating back to the instructors with questions about the items and suggestions for revisions. A primary objective was to produce a subset of items that were in category 3 or 4 (transfer items). For example, P.P.L. often asked the instructors whether particular problem types were practiced in class and made suggestions concerning how to shift the questions toward categories 3 or 4. Typically, this process went through one iteration, but the instructors and P.P.L. exchanged feedback on some exam items more than once. The process was considered complete when the instructors and P.P.L. agreed on all items’ ratings and when each exam contained at least five strong category 3/4 candidates. Next, the instructors finalized the exams and administered them to students. Following the exams, the instructors identified three problematic items that students interpreted in unintended ways or for which the correct answer did not completely capture minor irregularities in presented data (and accordingly the instructor accepted all answers). These three items were not considered in the analyses (one retention item and two transfer items; one of those transfer items was from exam 2 in Bio 1108, resulting in four scored transfer items for that exam). Table 2 provides the final composition of each of the exams (along with the category 2 “indeterminate” items that were not included in the present analyses), and basic descriptive statistics of the performances within each category of item (retention, transfer, indeterminate).1
| Course | Exam | Retention items | Transfer items | Indeterminate items | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. of items | M (SD) | Min. | No. of items | M (SD) | Min. | No. of items | M (SD) | Min. | ||
| BIOL 1107 | Exam 1 | 7 | 0.75 (0.18) | 0.29 | 7 | 0.74 (0.20) | 0.14 | 6 | 0.76 (0.19) | 0.17 |
| Exam 2 | 7 | 0.72 (0.14) | 0.29 | 5 | 0.54 (0.22) | 0.00 | 9 | 0.78 (0.16) | 0.33 | |
| Exam 3 | 1 | 0.95 (0.21) | 0.00 | 13 | 0.72 (0.20) | 0.23 | 6 | 0.79 (0.18) | 0.33 | |
| Exam 4 | 6 | 0.72 (0.18) | 0.17 | 6 | 0.73 (0.24) | 0.17 | 8 | 0.74 (0.15) | 0.12 | |
| BIOL 1108 | Exam 1 | 5 | 0.96 (0.10) | 0.60 | 8 | 0.71 (0.13) | 0.50 | 6 | 0.96 (0.08) | 0.67 |
| Exam 2 | 5 | 0.86 (0.16) | 0.40 | 4 | 0.92 (0.16) | 0.25 | 9 | 0.86 (0.10) | 0.67 | |
| Exam 3 | 5 | 0.94 (0.11) | 0.60 | 9 | 0.77 (0.16) | 0.33 | 6 | 0.92 (0.11) | 0.67 | |
| Exam 4 | 5 | 0.81 (0.18) | 0.40 | 9 | 0.82 (0.14) | 0.33 | 5 | 0.89 (0.15) | 0.60 | |
Concept-Building Task.
To index students’ concept-building approach (classifying them as exemplar or abstraction learners) independently of the course content, we assigned the same concept-building task used in previous studies (McDaniel et al., 2014, 2018; Frey et al., 2017, 2020). So that students would have no prior knowledge about the task, they were told to imagine that they were going to study an organism found on Mars that absorbs an element called Zebon and releases an element called Beros. The students’ objective was to learn to predict an output variable (amount of Beros released) based on an input variable (amount of Zebon absorbed). Unbeknownst to the participants, these input–output points followed an inverted-V function.
In the first phase, students were given between 200 and 260 training trials. For each training trial, students were presented with an input (a bar representing the amount of Zebon absorbed), had to predict the output (adjusted a bar to predict the amount of Beros released), and were given feedback (a bar reflecting the correct quantity of Beros and written specification of the prediction error). See Figure 1 for a sample trial.
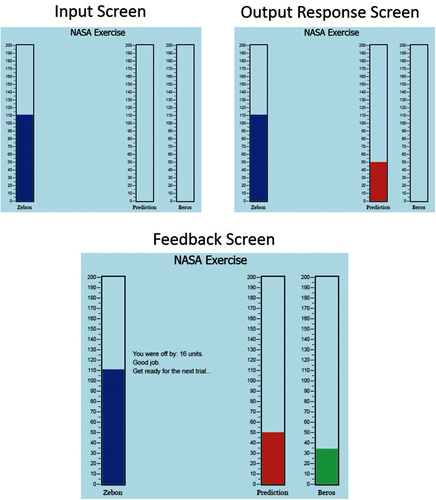
FIGURE 1. Screen shots of a trial from the concept-building task. The top left screen shows the initial display with the input. The top right shows the screen after the participant enters a prediction for the output. The bottom screen shows the feedback provided after the prediction is entered. Reprinted from Figure 1 in Frey et al. (2017). Copyright © 2017 American Chemical Society and Division of Chemical Education, Inc.
Participants were given as much time as they needed on each trial. Training consisted of 20 unique input values (all the odd numbers between 61 and 99), and trials were presented in 10–13 blocks (see end of paragraph for details). Each block consisted of 20 trials, presenting each of the input values once. A random order was created for each block, such that the order of input values differed across training block, with input order constant for all participants for each block. At the conclusion of a training block, participants were given their mean prediction error (MAE) for the block. Beginning with block 2, participants also saw their MAE from the previous block and a corresponding message. Those who had reduced their error were told: “Your accuracy IMPROVED. Keep up the good work!” Those whose error did not improve were told: “Your accuracy DID NOT IMPROVE. Keep working to improve your predictions!” Participants completed at least 10 training blocks (200 trials); training ended for participants with MAE < 10 on the 10th training block. For participants not meeting this criterion, training continued for up to three additional training blocks; training ended if the MAE fell below 10 in either blocks 11 or 12. Participants not meeting criterion in blocks 10–12 received one more training block (block 13: 260 trials total).
Upon completing training, participants began the test phase. In the test phase, they predicted the outputs for novel (untrained) inputs. Thirty of the inputs reflected extrapolation trials, and six reflected interpolation trials (36 total test trials). The extrapolation trials consisted of odd-numbered inputs outside the training domain (all odd numbers between 31 and 59 and between 101 and 129). The interpolation trials consisted of even-numbered inputs within the training domain (94, 80, 64, 88, 100, and 72). The test phase paralleled the training phase, except that participants received no feedback on the accuracy of their responses. Participants instead saw a message that said “Prediction Recorded. Get ready for the next trial.” The training and test phases combined took participants approximately 40 minutes to complete.
Following prior studies (McDaniel et al., 2014, 2018; Frey et al., 2017, 2020), classification of a participant’s concept-building approach was limited to participants with final training block MAE less than 10 (“learners”). This cutoff was established by initial work indicating that participants with MAE ≥ 10 for the final training block showed response patterns that deviated noticeably from the criterion values (shown in McDaniel et al., 2014, Figure 3, top panel), reflecting incomplete or poor learning. The same pattern is evident for participants in the current study (displayed in Supplemental Figure S1). The participants’ (those with MAE ≥ 10) final training block predictions varied little across the input values, resulting in a flat prediction curve that deviated substantially from the inverted-V target function. These participants (with relatively high final training block MAEs ≥ 10) could not be classified, because with incomplete learning, transfer patterns are not diagnostic of a particular learning approach; 88 participants in the sample exceeded the learning criterion and thus were not included in the main analyses. The remaining participants’ (N = 67) extrapolation MAEs were used to evaluate their correspondence to the extrapolation MAE derived from a simple exemplar model (as in McDaniel et al., 2018; Frey et al., 2020). The simple exemplar model (no generalization from input or output nodes; McDaniel and Busemeyer, 2005) predicts flat extrapolation extending from the end points of the training domain (the dashed horizontal lines in Figure 2). In particular, for the function used in this research, the simple exemplar model responds with an output of 148 for every extrapolation trial; the resulting MAE = 34.72 (error relative to the inverted-V function that generated the input–output points). Note that any set of predictions that average 148 and never overestimate the output value produce an MAE of 34.72.
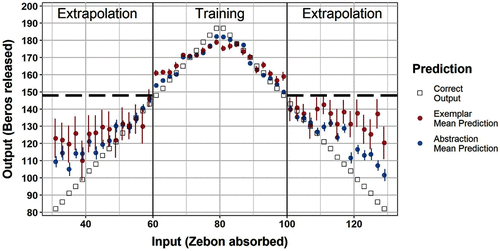
FIGURE 2. Mean exemplar learner predictions and abstraction learner predictions for final training block and extrapolation trials. Learners with all or part of their 95% CI greater than 34.72 in extrapolation (the MAE value for extrapolation based on an exemplar model; see text for details) were classified as exemplar learners. Learners with their entire 95% CI in extrapolation less than 34.72 (extrapolation tending toward the function rule) were classified as abstraction learners. Error bars represent the standard error of the mean.
Learners’ concept-building approaches were determined by comparing their extrapolation MAE and surrounding 95% confidence interval (CI) to this 34.72 value. Learners with all or part of their 95% CI greater than 34.72 were classified as exemplar learners, and learners with their entire 95% CI less than 34.72 were classified as abstraction learners. Past work has established that the classification of the two groups based on the MAE scores does reflect a bimodal distribution of MAE scores not simply a partitioning of a unimodal distribution of extrapolation performances (displayed in Figure 9, McDaniel et al., 2014). The exemplar learners’ training performances (last block MAE) clearly showed that they learned specific input–output associations, but their extrapolation MAEs indicted they did not abstract the appropriate function rule (their extrapolation was relatively flat, like a simple exemplar model, especially on the right side; see Figure 2). By contrast, the abstraction learners presumably extracted some rule-based information (i.e., the underlying function) in learning the training trials, allowing them to significantly outperform a simple exemplar model in extrapolation. Examination of Figure 2 confirms that the abstraction learners demonstrated extrapolation that followed the function.
Measure of General Intellectual Ability.
We collected two measures of intellectual ability. One was ACT score, or if not available, SAT score (which we translated into concordant ACT composite score). SAT, and by extension ACT (because the two are highly concordant), can be considered a measure of general intelligence (for the relation between IQ and standardized achievement tests, see Frey and Detterman, 2004; also Duckworth et al., 2012), as well as scholastic achievement. A second measure was the RAPM, considered to index fluid intelligence, another component of general cognitive ability (the RAPM and SAT are correlated, but the two do not overlap substantially; r = 0.48 [Frey and Detterman, 2014, experiment 2]). In the RAPM, a matrix of related patterns is displayed (typically a matrix of nine patterns), with the final pattern missing. Respondents have to pick one of eight possible options to complete the matrix. We gave students the shortened version of the RAPM (Bors and Stokes, 1998); they completed 12 trials (this version also has a “do not know” option) in self-paced manner, with a final score reflecting the proportion of 12 items they got correct. The task took approximately 10 minutes to complete.
Software and Analysis Details
R v. 4.1.0 (R Core Team, 2021) was used for all analyses. Between-subjects analyses of variance (ANOVAs) were conducted with the base aov function with contrasts set to c(“contr.sum”, “contr.poly”). Mixed-effects models were conducted with the lmer function from the package lmerTest (v. 3.1.3; Kuznetsova et al., 2017), which extends the lmer function from the package lme4 (v. 1.1.27; Bates et al., 2015) by allowing significance tests to be conducted on the output. The anova function from lmerTest was used to generate type III sums of squares ANOVA tables of fixed effects from lmer output, and the degrees of freedom were computed using the Kenward-Roger method (note that this accepted method of determining degrees of freedom sometimes gives degrees of freedom that diverge somewhat from conventional ANOVA models; e.g., as computed in SPSS). Effect sizes, Sum of squares (SS) Error, mean squared (MS) Error, and partial eta-squared were computed manually based on the information available in the output of anova. The emmeans package (v. 1.6.1; Lenth, 2021) was used to conduct follow-up analyses for both aov and lmer models, with the ref_grid function used to generate estimated marginal means and the contrast function used to conduct pairwise contrasts. For lmer models, contrast degrees of freedom were calculated using the Kenward-Roger method. Plots were generated with the ggplot2 package (v. 3.3.3; Wickam, 2016), with assistance from the emmip function from emmeans.
RESULTS
We first examined whether students identified as abstractor learners were characterized by higher levels of general intellectual ability, as assessed by composite ACT scores and by RAPM scores, than students identified as exemplar learners. Abstractor and exemplar learners did not statistically differ on either composite ACT scores, Ms = 28.75 and 27.71, respectively; t(145) = 1.28, p = 0.408; or RAPM scores, Ms = 6.52 and 5.67, respectively, t(127) = 0.99, p = 0.587.2 Further, exemplar learners were not students at the lower end of general intellectual ability relative to other students in the class. The exemplar learners scored nominally higher than the remaining students in the class (i.e., those whose learning approach could not be determined, because they did not meet the learning criterion on the function-learning task) on both composite ACT (M = 26.69; p = 0.354) and RAPM (M = 5.04; p = 0.726). These patterns reinforce prior reports indicating that general intellectual ability is not necessarily a proxy or determinant of students’ tendencies to learn and represent concepts in a relatively more abstraction-based versus exemplar-based manner (Frey et al., 2017; McDaniel et al., 2018). Still, the nonsignificant differences in general intellectual ability (ACT and RAPM) favored the abstraction over the exemplar learners. Accordingly, we included those indices as covariates in the statistical analyses of exam performances to ensure that any effects of students’ concept-building approaches were not a consequence of intellectual ability per se.
Exam Performance
Exam performance was analyzed as a function of concept-building approach (exemplar, abstraction) and question type (retention, transfer). To account for the within-subjects nature of question type, mixed-effects models were conducted with a random effect of student (i.e., the intercept was allowed to vary across student). In an initial model, concept-building approach, question type, and ACT scores were included as fixed effects, as well as question type by concept-building and question type by ACT interaction terms. Before being entered into the model, ACT scores were first centered by subtracting the mean value of 27.45.
In general, abstraction learners outperformed exemplar learners, F(1, 62) = 8.46, mean squared error (MSE) = 0.005, p = 0.005, ηp2 = 0.12; but this main effect was qualified by a significant interaction with question type, F(1, 62) = 16.58, MSE = 0.005, p < 0.001, ηp2 = 0.21.3 The estimated marginal means for this interaction are displayed in Figure 3. This figure shows that abstraction and exemplar learners performed nearly identically on the retention questions (M = 0.83 and 0.81, respectively), but abstraction learners performed notably better on the transfer questions than did exemplar learners (M = 0.82 and 0.68, respectively). Simple contrasts confirm that abstraction and exemplar learners performed equivalently on retention questions, t(96) = 0.60, p = 0.550; but abstraction learners significantly outperformed exemplar learners on transfer questions, t(96) = 4.51, p < 0.001. ACT performance was not significantly related to exam performance in general, F(1, 62) = 3.03, p = 0.087; but did interact with question type, F(1, 62) = 4.17, MSE = 0.005, p = 0.046, ηp2 = 0.06. This interaction results from the slope between ACT and performance being significantly more positive for transfer items (0.011) than for retention items (0.002). Clearly, however, the interaction of ACT and question type represented a smaller effect (which met the convention of ηp2 = 0.06 for a medium-size effect) than the interaction of concept-building approach with question type (which exceeded the convention of ηp2 = 0.14 for a large-size effect). Finally, performance on retention questions was better than that on transfer questions, F(1, 62) = 38.46, MSE = 0.005, p < 0.001, ηp2 = 0.38.
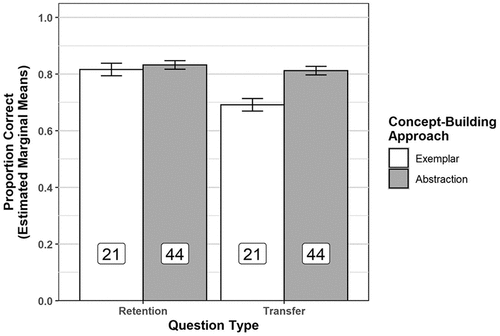
FIGURE 3. Transfer and retention performance as a function of concept-building approach with ACT accounted for. Estimated marginal means are from a model including the main effect of ACT and ACT by question type interaction. Error bars represent the standard error of the mean. Labels inside bars represent the sample size for the condition.
We next added RAPM (centered by subtracting the mean value of 5.59) as a second covariate (in addition to ACT) to the foregoing analysis to evaluate whether this aspect of intellectual ability (i.e., fluid intelligence) might underlie or account for the effects of concept-building approach on exam performance. RAPM did not relate to exam performance in general, F(1, 53) = 1.24, p = 0.27; but did significantly interact with question type, F(1, 53) = 7.29, MSE = 0.004, p = 0.009, ηp2 = 0.12. This interaction reflects that the slope between RAPM and performance was nearly flat for transfer questions (0.001) but actually negative for retention questions (−0.011). ACT also still interacted with question type, F(1, 53) = 5.19 MSE = 0.004, p = 0.027, ηp2 = 0.09. Despite the additional intellectual ability factor interacting with question type, the interaction of concept-building approach with question type remained robust, F(1, 53) = 8.71, MSE = 0.004, p = 0.005, ηp2 = 0.14, showing a pattern nearly identical to that described earlier for simple contrasts, confirming that the advantage of abstraction learners was significant for transfer items t(81) = 4.46, p <0.001; but not retention items, t(81) = 1.66, p = 0.10 (see Figure 4).
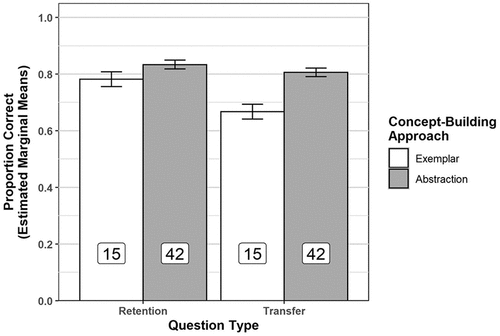
FIGURE 4. Transfer and retention performance as a function of concept-building approach with ACT and RAPM accounted for. estimated marginal means are from a model including the main effects of ACT and RAPM and ACT by question type and RAPM by question type interactions. Error bars represent the standard error of the mean. Labels inside bars represent the sample size for the condition.
In a final set of comparisons we examined whether the patterns on the individual exams were fairly stable in terms of reflecting the overall differences in transfer items (and no differences in retention items) across exemplar and abstraction learners. As can be seen in Figure 5,4 exemplar and abstraction learners performed equivalently on retention items on every exam. Pairwise contrasts confirmed that, for each exam, there was no significant difference on retention items between exemplar and abstraction learners (all t values < 1, all p values > 0.35). For transfer items, Figure 5 shows that the advantage for abstraction learners (relative to exemplar learners) was generally stable across exams, though perhaps diminished on the first exam. Pairwise contrasts revealed that indeed exemplar and abstraction learners did not significantly differ on exam 1 (t = 1.32, p = 0.19). The difference became significant by exam 2 and remained robust for subsequent exams (t values varied from 3.41 to 3.60, all p values < 0.001). Thus, the differential group differences across retention and transfer items were largely stable over the duration of the course.
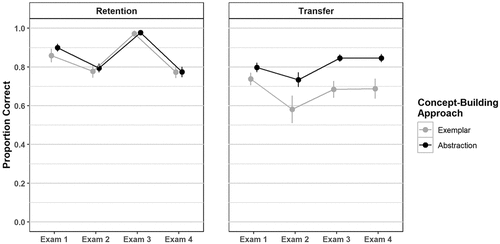
FIGURE 5. Transfer and retention performance as a function of exam and concept-building approach. Points represent the descriptive mean of proportion correct for the given level concept-building approach, exam, and question type. These means are from the 21 exemplar learners and 44 abstraction learners with complete exam and ACT data. Points are offset horizontally to avoid overlapping between exemplar and abstraction points for a given exam. Error bars represent standard error of the mean.
DISCUSSION
An overarching goal for many introductory biology courses is to assist students with developing a deep, conceptual understanding of core concepts. One way to evaluate the degree to which this educational goal has been reached is to include transfer questions on summative assessments, an approach that has been increasingly emphasized by biology educators (e.g., Handelsman et al., 2004; Bissell and Lemons, 2006; Crowe et al., 2008; Pfund et al., 2009; American Association for the Advancement of Science, 2011; Ebert-May et al., 2015; Laverty et al., 2016). Moreover, many efforts to improve students’ conceptual understanding and, as a consequence, performance on transfer-based questions, have focused on a variety of instructional approaches (e.g., improving visual representations: Novick and Catley, 2007, 2013; fostering productive failures: Kapur, 2014, 2016; guided inquiry: Hmelo-Silver et al., 2007; and more active-learning techniques in general: Freeman et al., 2014; Halmo et al., 2020). In this article, we focused on another potentially critical factor in determining the degree to which biology students will display transfer of instructed concepts (i.e., good performance on assessment questions targeting transfer): individual differences in how learners in introductory biology classes acquire and represent concepts.
Appealing to recent basic cognitive science research (Juslin et al., 2003; Bourne et al., 2010; Hoffmann et al., 2014; McDaniel et al., 2014; Little and McDaniel, 2015), as developed in the Introduction, our central idea is that some learners tend to focus on exemplar-based representations of the instructed concepts, whereas other learners tend to focus on more abstract underpinnings. These qualitatively different representations would theoretically be expected to impact the degree to which the concepts can be transferred (e.g., McDaniel et al., 2014; see also Gick and Holyoak, 1980; Frey et al., 2020). Exemplar-based representations would be expected to be based on surface features of problems and instructional examples, and to be rich in characteristics that are idiosyncratic to the particular study examples (cf. Regehr and Brooks, 1993). Such representations tend to limit transfer to novel questions and problems (Gick and Holyoak, 1980; McDaniel et al., 2014). In contrast, abstract representations reflect deep-structure characteristics of problems, characteristics that support transfer (Gick and Holyoak, 1983).
The foregoing theoretical analysis directly anticipates and aligns with the central results of the present study. Those biology students who displayed abstraction-based learning tendencies (as indexed independently by a laboratory learning task unrelated to the biology course or to biology content in general) showed substantially better performance on the transfer exam questions than the biology students who displayed exemplar-based learning tendencies. In sharp contrast, on retention exam questions—questions that echoed the particular instantiations of the concepts reflected in the instruction (class, textbook, or homework)—the abstraction- and exemplar-based learners performed identically. Moreover, students with abstraction-learning tendencies maintained good performance across retention (83%) and transfer (82%) questions, whereas those with exemplar-learning tendencies showed a notable decline from their relatively good performance on retention questions (81%) to their performance on transfer questions (68%). This pattern further converges with the theoretical interpretation that the students identified as abstraction learners tended to construct a deep understanding of the concepts (presumably based on abstract underpinnings), thereby enabling them to apply and generalize the concepts to scenarios and instantiations not seen during instruction. The exemplar learners were less able to generalize the target concepts, consistent with the idea that their representations were presumably based on the instructed examples; that is, these students were apparently memorizing the instructed examples as the basis for their learning (e.g., see Frey et al., 2020).
Our interpretation of the differences in transfer-question performance emphasizes individual differences across students in the conceptual representations that they construct. Another possible interpretation of the pattern is that these students’ conceptual representations were not substantially different; instead, it may be that the students differed in their general ability to figure out how the examples highlighted during instruction (classroom, textbook, or homework) related to and aligned with the transfer exam questions. To explore this possibility, we collected two indices of general intellectual ability for the participants that typically are assumed to capture reasoning and thinking skills (ACT and RAPM, an index of fluid intelligence). Several suggestive patterns emerged. Though both ACT and RAPM significantly interacted with type of exam question, the interaction patterns were not consistent. Only the ACT index was associated with performance on transfer questions (a positive association). Thus, the idea that general intellectual ability may be related to transfer performance could be too broad; perhaps a relation between general intelligence and transfer in STEM learning is restricted to crystallized intelligence (in part, accrued knowledge).
Critically, however, this dynamic associated with the ACT index very likely did not account for the superior transfer performance of abstraction relative to exemplar learners. One clear reason is that concept-building tendency significantly interacted with type of exam question when the variance accounted for by ACT (and RAPM) was taken into account. Indeed, the interaction between concept-building tendency and exam question type remained a large-size effect in the presence of the ACT (and RAPM) covariate (and the interaction between ACT and exam question type was only a medium-size effect). A second reason is exemplar learners did not differ significantly from abstraction learners on ACT and RAPM scores. That is, exemplar learners did not display lower general ability than abstraction learners; in fact, exemplar learners as a group were not at the lower end of the ACT and RAPM spectrum relative to the rest of the students in the class (students who were not able to be classified as exemplar/abstractor learners on the laboratory learning task).
The idea that students differ in their tendency toward constructing conceptual representations that are more exemplar or abstraction based and that these differences play a key role in STEM learning, exam performance, and problem solving is reinforced by similar results with general chemistry students’ exam performances on retention and transfer questions (McDaniel et al., 2018), general chemistry students’ problem-solving performance (Frey et al., 2020), and superior performance in organic chemistry (where abstract conceptual representations should advantage performance; Frey et al., 2017). The current results in introductory biology reflect an important extension for a number of reasons. First, in the general chemistry study (McDaniel et al., 2018), exam questions and problems were typically quantitative in nature, and the laboratory learning task was a function-learning task based on quantitative relations. Thus, it is possible that these individual differences were restricted to quantitative-type concepts (though laboratory work has not indicated this to be the case; McDaniel et al., 2014). The biology exam questions were not quantitative in nature, though a subset of eight questions required interpreting graphs and tables and noticing data patterns. Thus, the present finding in concert with recent case study findings on qualitative general chemistry problems (Lewis structure problems; Frey et al., 2020) establishes that the differences in abstraction and exemplar building tendencies indexed by the laboratory learning task are not limited to quantitatively based problems.
Second, the present study sampled from a more diverse student population than previous studies conducted at selective private institutions (McDaniel et al., 2018; Frey et al., 2020). Third, we reinforced that variations in crystallized intelligence (ACT) do not underlie the influence of concept-building approach on exam performances (see also Frey et al., 2017; McDaniel et al., 2018) and showed that fluid intelligence (as indexed by RAPM) also does not underlie the relation between concept-building approach and exam performance.
A fourth important extension of the current study is that both biology instructors employed an array of active-learning methods. As outlined in the Introduction, a general objective for these courses was to foster deep learning of the concepts as opposed to memorization of the instructional examples. Indeed, one of the instructors (coauthor L.B.L.) explicitly told her students that she would not test them on the details of cases discussed in class, because the purpose of class was to practice applying concepts, not to memorize the details of examples. Nevertheless, individual differences in concept-building tendencies appeared to override the class’s emphasis on understanding and applying concepts: Those with exemplar-learning tendencies performed well on retention exam questions (which echoed the class presentations, class activities, or homework) but less well on transfer exam questions—for which memorization of class content (without deeper understanding/abstraction) would be less helpful.
Finally, it is intriguing to reconsider existing findings on learner sensitivity to item context in light of the current study. A substantial body of research on science learning shows that student performance on science assessments is influenced by contextual features of the items (e.g., Chi et al., 1981; Clough and Driver, 1986; Clark, 2006; Sabella and Redish, 2007; Bryce and MacMillan 2009). This pattern was reinforced in a controlled study of item context features in the assessment of natural selection (Nehm and Ha, 2011). Undergraduates enrolled in an introductory biology course completed an assessment of natural selection in which the item contexts varied. Items asked about evolutionary trait loss or gain and required comparisons between species or within species. Students provided a significantly greater number of naïve biological ideas on items involving evolutionary trait loss compared with items involving evolutionary trait gain. Similarly, students provided a significantly greater number of naïve biological ideas for items involving between-species comparisons than within-species comparisons. A possible extension of the present results is that abstraction learners might be more likely to respond equivalently across item contexts, because they search for and apply the underlying principles of science phenomena. In contrast, exemplar learners might be more likely to respond differentially to items based on context, because they attend to the specifics of learned examples. Further research could test this hypothesis.
Limitations
There are also several limitations to the study that bear noting. The data were collected at one large public university; it would be informative to replicate the present patterns at other universities with varying student characteristics, enrollment sizes, funding (public, private), and approaches to introductory biology. Further, even within the present sample, slightly more than 50% of the students who completed the assessment could not be classified in terms of their concept-building approach, because they did not meet the learning criterion (MAE ≥ 10) on the training portion of the assessment. We suspect that the primary reason students did not meet the learning criterion was a lack of sufficient effort, likely in part because the assessment was delivered online. To examine this possibility, we developed three markers of low effort: 1) averaging < 2.5 seconds per trial, 2) using fewer than five unique prediction values across training blocks 6–10 (the last five training blocks), and 3) showing a large (≥5) block-wise MAE increase in at least one of blocks 6–10. We then tabulated the percentage of non-learners and learners who displayed at least one of these markers of low effort. Sixty-seven percent of non-learners but only 7.5% of learners displayed markers of low effort, suggesting that low effort was a primary factor in students not reaching the learning criterion. Further, their low effort appeared to be limited to this assessment; average performances for the non-learners on course exams were comparable to those of exemplar and abstraction learners on retention items (except for exam 1, where non-learners performed less well) and to those of exemplar learners on transfer items (see Supplemental Figure S2).
In previous studies, when students have been given the task in person, the proportions of students who do not meet the learning criterion (and thus could not be classified) have been much lower (ranging from 8% to 21% in three research lab studies, McDaniel et al., 2014; and 23% in a classroom setting, Frey et al., 2020). These in-person patterns suggest that, if the students in the biology classes had been administered the task under supervision, a large majority would likely have been characterized in terms of the two concept-building approaches identified herein. In the present study, students could elect to not take the task seriously without feeling social pressure or being penalized. The assessment is challenging, and it requires that students work sufficiently hard to meet the learning criterion. This requirement may limit the extent to which the assessment can classify all or nearly all students’ concept-building approach in classroom research where students complete the assessment online. It thus remains possible that the present patterns could change if students who do not complete the assessment could somehow be classified in terms of concept-building approach.
Another outstanding issue is whether exemplar and abstraction learners differed in biology background knowledge at the outset of the course. For instance, if abstraction learners had more prior biology knowledge, this could have advantaged their exam performances relative to exemplar learners. We did not assess background knowledge; thus, the present findings do not directly inform this possibility. Several observations, however, are not entirely consistent with the possibility that differential background knowledge mediated the current patterns. First, exemplar and abstraction learners showed equivalent performance on retention items in the present study. This pattern does not align with a differential background knowledge interpretation inasmuch as differential background knowledge could impact performance across a range of exam item types. Second, on the initial exam in the course, when background might be expected to exert influence, transfer performance did not significantly differ across exemplar and abstraction learners.
Instructional Implications
An outstanding question is what instructional techniques might be implemented to assist students with exemplar concept-building tendencies to develop a more abstract, generalizable representation of the instructed concepts.5 As far as we are aware, no published work has directly targeted this question. Nevertheless, in this final section, we appeal to the educational and cognitive science literatures to offer some tentative suggestions to guide further research and instructional efforts.
Productive Failure.
One idea is to design exercises or assignments that lead to “productive failure” (Kapur, 2014, 2016; Halmo et al., 2020). Such assignments require students to explore and generate possible solutions to problems on their own before receiving direct instruction on the concepts and procedures (Schwartz et al., 2011; Kapur, 2014). Problems are designed so that students fail to generate correct solutions on their own, but the failure is purposeful, enabling students to activate and differentiate prior knowledge, recognize knowledge gaps, and focus attention on the problems’ underlying conceptual structure (Kapur, 2016; Loibl et al., 2017). This approach is intended to avoid a possible drawback of instructing with worked examples: Students may merely apply provided procedures to problems without understanding the concepts in a way that allows them to transfer their knowledge to new situations (Schwartz et al., 2011). Initial research shows a promising advantage of the productive failure approach over more conventional approaches for stimulating acquisition of conceptual knowledge (underlying abstractions) and supporting transfer (Schwartz et al., 2011; Kapur, 2014; Loibl et al., 2017). Whether this advantage extends to students with exemplar-learning tendencies awaits future work.
Problem Homework.
Problem homework could be designed to stimulate students to consider and focus on the conceptual underpinnings of practice problems. One technique would be to pose deep-level questions such as “Why?” and “How?” concerning aspects of the problem. For instance, students might be asked “Why is this a key problem?” or “How does the problem relate to concepts covered in the course?” An array of evidence suggests that the construction of explanations by the students produces learning gains in science learning on assessments that tap deep knowledge (for a review, see Pashler et al., 2007). A related technique could be to focus on the reasoning for the particular solutions that the students try. That is, the students are prompted to generate self-explanations—to answer why particular steps are used to solve a problem (Chi et al., 1989; Wylie and Chi, 2014; for a laboratory experiment supporting the potential effectiveness of this technique, see deBruin et al, 2007).
Conceptual Questions.
Much of the content in biology focuses on problems that do not require computational operations (unlike some general chemistry courses) and instead rely predominately on prediction, explanation, and conceptual reasoning. For this content, instructors might guide students to generate and answer conceptual questions—questions that focus on knowledge about a target concept or require integration across various concepts and principles. Findings show that college learners can successfully pose such questions when instructed to do so (e.g., Bugg and McDaniel, 2012; Lin et al., 2018). Moreover, in a laboratory experiment, learners instructed to generate and answer the conceptual questions performed substantially better on a final concept-oriented test than did learners who studied (without question generation) or who generated and answered detail questions (Bugg and McDaniel, 2012). Again, it remains to investigate this technique for students with exemplar-learning concept-building tendencies in particular.
FOOTNOTES
1 A reviewer requested information about the reliability of the exams. Because there were no test–retest scores (as is typical with classroom exams) from which to compute reliability, we computed Cronbach’s alpha for all retention items and all transfer items combined across the four exams within each course (using all consenting participants with full exam scores who completed the concept-building task). (Cronbach’s alpha indexes the degree to which all items on a test measure the same construct, and is commonly reported in measurement development; Henson, 2001.) For retention items, alpha was 0.49 and 0.40 for the first- and second-semester exams, respectively; for transfer items, alpha was 0.78 and 0.50 for first- and second-semester exams, respectively. However, as argued elsewhere (e.g., Solomon et al., 2021), internal consistency is not wholly appropriate for evaluating the reliability of a test in which the items cover a range of content: One may not expect that a student would perform similarly across that range because the student may have a good understanding of some content but not other content. Test–retest reliability would be a more informative index of the exams’ stability; indeed, see Solomon et al. (2021) for high test–retest reliability of a knowledge assessment (like an exam) in the face of relatively low Cronbach alpha values.
2 These analyses included those students whose learning approach could not be determined, because they did not meet the learning criterion on the function-learning task. Accordingly, the degrees of freedom reflect the total sample of students who completed the function-learning task and for whom ACT scores (or converted SAT scores) were available or completed both the function-learning and RAPM tasks. The p values are Tukey adjusted.
3 We conducted a model that included all 67 participants with a concept-building classification (reflected in Figure 2) and removed the ACT fixed-effects terms. This model produced results identical to that when the ACT terms were included: abstraction learners outperformed exemplar learners, F(1, 65) = 9.02, MSE = 0.004, p = 0.004, ηp2 = 0.12; but this effect was limited to transfer questions, F(1, 65) = 20.22, MSE = 0.004, p < 0.001, ηp2 = 0.24; performance on retention questions was better than that on transfer questions, F(1, 65) = 78.00, MSE = 0.004, p < 0.001, ηp2 = 0.55.
4 Note that averaging across the individual exam scores does not produce grand means that are identical to those displayed in Figure 3 and reported in the text. This is because the numbers of retention and transfer items varied for each individual exam, so a direct average of the four exams produces an unweighted (by number of items) index. By contrast, the primary analyses computed overall semester performances by totaling the number of exam items of a given type (retention, transfer) across the semester (rather than averaging performance across each exam score).
5 The (untested) assumption here is that, with appropriate instruction, at least some exemplar learners might be able to develop effective abstractions for much (or all) of the instructed concepts. The assumption seems plausible, given that the exemplar learners in the current courses showed sufficient abstraction to support average correct responses of 68% for the transfer items. However, this is not to imply that such instruction would necessarily alter the learner’s concept-building tendency in general (e.g., for other courses). Frey et al. (2017) administered the concept-building task to students in introductory chemistry 1 (in Fall 2012) and to students in organic chemistry 2 (Spring 2014). Forty-one students completed both assessments, and 85% of those students displayed the same concept-building approach across the 1.5 year interval. Thus, even after taking three semesters of various classes between the two assessment time points, these students’ concept-building approach appeared to be stable.
ACKNOWLEDGMENTS
We would like to acknowledge the participants for their time and effort. We kindly thank Erin Dolan for access to her classroom and participation as an instructor in the study. This material is based upon work supported by the National Science Foundation under grant no. DRL1350345.
REFERENCES
American Association for the Advancement of Science . (2011). Vision and change in undergraduate biology education: A call to action (p. 81). Washington, DC: American Association for the Advancement of Science. Google Scholar- , ... & (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. Boston: Allyn & Bacon. Google Scholar
- (2007). Cooperative learning in industrial-sized biology classes. CBE—Life Sciences Education, 6(2), 163–171. Link, Google Scholar
- (2018). Teacher knowledge for active-learning instruction: Expert–novice comparison reveals differences. CBE—Life Sciences Education, 17(1), ar12. Link, Google Scholar
- (2002). When and where do we apply what we learn? A taxonomy for far transfer. Psychological Bulletin, 128, 612–637. doi:
10.1037/0033-2909.128.4.612 Medline, Google Scholar - (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. doi:
10.18637/jss.v067.i01 Google Scholar - (2006). A new method for assessing critical thinking in the classroom. BioScience, 56(1), 66–72. Google Scholar
- (1998). Raven’s Advanced Progressive Matrices: Norms for first-year university students and the development of a short form. Educational and Psychological Measurement, 58, 382–398. Google Scholar
- (1974). An inference model of conceptual rule learning. In Solso, R. L. (Ed.), Theories in cognitive psychology: The Loyola symposium (pp. 231–256). Potomac, MD: Erlbaum. Google Scholar
- (2010). Strategy selection and use during classification skill acquisition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 500–514. Medline, Google Scholar
- (2009). Momentum and kinetic energy: Confusable concepts in secondary school physics. Journal of Research in Science Teaching, 46(7), 739–761. Google Scholar
- (2012). Selective benefits of question self-generation and answering for remembering expository text. Journal of Educational Psychology, 104, 922–931. Google Scholar
- (1989). Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science, 13(2), 145–182. Google Scholar
- (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5(2), 121–152. Google Scholar
- (2006). Longitudinal conceptual change in students’ understanding of thermal equilibrium: An examination of the process of conceptual restructuring. Cognition and Instruction, 24(4), 467–563. Google Scholar
- (1986). A study of consistency in the use of students’ conceptual frameworks across different task contexts. Science Education, 70, 473–496. Google Scholar
- (2012). Whichever way you choose to categorize, working memory helps you learn. Quarterly Journal of Experimental Psychology, 65, 439–464. Medline, Google Scholar
- (2008). Biology in bloom: Implementing Bloom’s taxonomy to enhance student learning in biology. CBE—Life Sciences Education, 7(4), 368–381. Link, Google Scholar
- (2007). The effect of self-explanation and prediction on the development of principled understanding of chess in novices. Contemporary Educational Psychology, 32, 188–205. Google Scholar
- (1999). Correspondences between ACT and SAT I scores (College Board Report No. 99–91). New York: College Entrance Examination Board. Google Scholar
- (2012). What No Child Left Behind leaves behind: The roles of IQ and self-control in predicting standardized achievement test scores and report card grades. Journal of Educational Psychology, 104, 439–451. Medline, Google Scholar
- (2015). Breaking the cycle: Future faculty begin teaching with learner centered strategies after professional development. CBE—Life Sciences Education, 14(2), ar22. Link, Google Scholar
- (2014). Active learning increases student performance in science, engineering, and mathematics. Proceedings of the National Academy of Sciences USA, 111, 8410–8415. Medline, Google Scholar
- (2004). Scholastic assessment or g? The relationship between the Scholastic Assessment Test and general cognitive ability. Psychological Science, 15, 373–378. Medline, Google Scholar
- (2017). Students’ concept-building approaches: A novel predictor of success in chemistry courses. Journal of Chemical Education, 94, 1185–1194. Google Scholar
- (2020). Using students’ concept-building tendencies to better characterize average-performing student learning and problem-solving approaches in general chemistry. CBE—Life Sciences Education, 19, ar42 doi:
10.1187/cbe.19-11-0240 Link, Google Scholar - (1980). Analogical problem solving. Cognitive Psychology, 12, 306–355. Google Scholar
- (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1–38. Google Scholar
- (2011). Increased structure and active learning reduce the achievement gap in introductory biology. Science, 332(6034), 1213–1216. Medline, Google Scholar
- (2020). Advancing the guidance debate: Lessons from educational psychology and implications for biochemistry learning. CBE—Life Sciences Education, 19, ar41. Link, Google Scholar
- , … & (2004). Scientific teaching. Science, 304, 521–522. Medline, Google Scholar
- (2001). Understanding internal consistency reliability estimates: A conceptual primer on coefficient alpha. Measurement and Evaluation in Counseling and Development, 34, 177–189. Google Scholar
- (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42(2), 99–107. doi:
10.1080/00461520701263368 Google Scholar - (2014). Pillars of judgment: How memory abilities affect performance in rule-based and exemplar-based judgments. Journal of Experimental Psychology: General, 143, 2242–2261. Medline, Google Scholar
- (2020). Testing effect on high-level cognitive skills. CBE—Life Sciences Education, 19, ar39 doi:
10.1187/cbe.19-10-0193 Link, Google Scholar - (2014). Teaching to the test … or testing to teach: Exams requiring higher order thinking skills encourage greater conceptual understanding. Educational Psychology Review, 26, 307–329. Google Scholar
- (2021). A learning method for all: The testing effect is independent of cognitive ability. Journal of Educational Psychology, 113, 972–985.
https://doi.org/10.1037/edu0000627 Google Scholar - (2003). Exemplar effects in categorization and multiple-cue judgement. Journal of Experimental Psychology: General, 132, 133–156. Medline, Google Scholar
- (2016). Examining productive failure, productive success, unproductive failure, and unproductive success in learning. Educational Psychologist, 51, 289–299. doi:
10.1080/00461520.2016.1155457 Google Scholar - (2014). Productive failure in learning math. Cognitive Science, 38, 1008–1022. Medline, Google Scholar
- (2005). Teaching more by lecturing less. Cell Biology Education, 4(4), 298–310. Link, Google Scholar
- (1992). ALCOVE: An exemplar-based connectionist model of category learning. Psychological Review, 99, 22–44. Medline, Google Scholar
- (2017). lmerTest package: Tests in linear mixed effects models. Journal of Statistical Software, 82(13), 1–26. doi:
10.18637/jss.v082.i13 Google Scholar - , … & (2016). Characterizing college science assessments: The three-dimensional learning assessment protocol. PLoS ONE, 11(9), e0162333. Medline, Google Scholar
- (2021). emmeans: Estimated marginal means, aka least-squares means (R package version 1.6.1.). https://CRAN.R-project.org/package=emmean Google Scholar
- (2018). Effects of flashcards on learning authentic materials: The role of detailed versus conceptual flashcards and individual differences in structure-building ability. Journal of Applied Research in Memory and Cognition, 7, 529–539. Google Scholar
- (2011). Response-time tests of logical-rule models of categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition, 37, 1–27. Medline, Google Scholar
- (2015). Individual differences in category learning: Memorization versus rule-abstraction. Memory & Cognition, 43, 85–98. Medline, Google Scholar
- (2017). Towards a theory of when and how problem solving followed by instruction supports learning. Educational Psychology Review, 29(4), 693–715. Google Scholar
- (2012). Less teaching, more learning: 10-yr study supports increasing student learning through less coverage and more inquiry. Advances in Physiology Education, 36(4), 325–335. Medline, Google Scholar
- (2005). The conceptual basis of function learning and extrapolation: Comparison of rule and associative based models. Psychonomic Bulletin & Review, 12, 24–42. Medline, Google Scholar
- (2018). Individual differences in learning exemplars versus abstracting rules: Associations with exam performance in college science. Journal of Applied Research in Memory and Cognition, 7, 241–251. Google Scholar
- (2014). Individual differences in learning and transfer: Stable tendencies for learning exemplars versus abstracting rules. Journal of Experimental Psychology: General, 143, 668–693. Medline, Google Scholar
- (1978). Context theory of classification learning. Psychological Review, 85, 207–238. Google Scholar
- (2010). Just the facts? Introductory undergraduate biology courses focus on low-level cognitive skills. [Reports - Evaluative]. CBE—Life Sciences Education, 9(4), 435–440. Link, Google Scholar
National Research Council . (1996). National science education standards. Washington, DC: National Academies Press. Google Scholar- (2011). Item feature effects in evolution assessment. Journal of Research in Science Teaching, 48, 237–256. Google Scholar
- (1984). Choice, similarity, and the context theory of classification. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10, 104–114. Medline, Google Scholar
- (1988). Analogical transfer, problem similarity, and expertise. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14(3), 510–520. Medline, Google Scholar
- (2007). Understanding phylogenies in biology: The influence of a Gestalt perceptual principle. Journal of Experimental Psychology: Applied, 13, 197–223. doi:
10.1037/1076-898X.13.4.197 Medline, Google Scholar - (2013). Reasoning about evolution’s grand patterns: College students’ understanding of the tree of life. American Educational Research Journal, 50, 138–177. Google Scholar
- (2007). Organizing instruction and study to improve student learning (NCER 2007-2004). Washington, DC: National Center for Education Research, Institute of Education Sciences, U.S. Department of Education. Retrieved May 16, 2019, from http://ncer.ed.gov Google Scholar
- , ... & (2009). Summer institute to improve university science teaching. Science, 324(5926), 470–471. Medline, Google Scholar
- (1981). The relation between test intelligence and problem-solving success. Zeitschrift fur Psychologie mit Zeitschrift fur angewandte Psychologie, 189, 79–100. Google Scholar
- (1981). The predictability of complex problem solving by performance on an intelligence test. Zeitschrift fur Experimentelle and Andewandte Psychologie, 28, 309–334. Google Scholar
- (1991). Manual for Raven’s Progressive Matrices and Vocabulary Scales, Section 1, General overview. Oxford, UK: Oxford Psychologists Press. Google Scholar
R Core Team (2021). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org Google Scholar- (1993). Perceptual manifestations of an analytic structure: The priority of holistic individuation. Journal of Experimental Psychology: General, 122, 92–114. doi:
10.1037/0096-3445.122.1.92 Medline, Google Scholar - (2007). Knowledge organization and activation in physics problem solving. American Journal of Physics, 75, 1017–1029. Google Scholar
- (2011). Practicing versus inventing with contrasting cases: The effects of telling first on learning and transfer. Journal of Educational Psychology, 103, 759–775. doi:
10.1037/a0025140 Google Scholar - (2021). Development and validation of an introductory psychology knowledge inventory. Scholarship of Teaching and Learning in Psychology, 7, 123–139. Google Scholar
- (2005). Complex problem solving and intelligence: Empirical relation and causal direction. In Sternberg, R. J., Pretz, J. E. (Eds.), Cognition & intelligence: Identifying the mechanisms of the mind (pp. 160–187). New York: Cambridge University Press. Google Scholar
- (2016). ggplot2: Elegant graphics for data analysis. New York: Springer-Verlag. Google Scholar
- (2014). The self-explanation principle in multimedia learning. In Mayer, R. E. (Ed.), The Cambridge handbook of multimedia learning (2nd ed., pp. 413–432). New York: Cambridge University Press. Google Scholar